trójkat
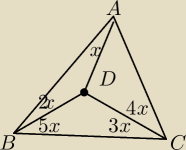
iwo: We wnętrzu trójkąta równoramiennego ABC (∡ B = ∡C) znajduję się punkt punkt D taki, że
∡ DAB = α, ∡ DBA = 2α, ∡ DBC = 5α, ∡ DCB = 3α, ∡ DCA = 4α. Oblicz miary kątów trójkąta
ABC.
13 lip 21:55
Mila:
Czy te kąty dobrze są napisane?
15 lip 22:26
an: α=10o i bawcie się
16 lip 13:02
iwo:
16 lip 13:41
iwo: Tak są dobrze przepisane
16 lip 13:41
iwo: To zadanie z kangura
16 lip 17:38
iwo: więc dość trudne
16 lip 23:09
ite:
doszłam do równania sin(α) + sin(5α) = sin(11α) ale to nie jest zabawne : (
16 lip 23:48
Mariusz:
Ciekawe czy taki pomysł by zadziałał ?
Niech punkt E będzie przecięciem odcinka AB i przedłużenia odcinka CD
Spróbuj pokazać że ACE jest równoramienny
17 lip 05:11
Mariusz:
Gdyby na odcinku BD odłożyć kąt x wtedy drugie ramię kąta x przecięłoby odcinek CD w punkcie E
i teraz należałoby pokazać podobieństwo trójkątów BEC oraz ADC
17 lip 06:26
Mariusz:
Jeżeli to jest kangur z tego roku to pewnie ci to zadanie usuną
Spróbuj może na obcojęzycznych forach najlepiej tam gdzie polacy nie wchodzą
17 lip 07:38
17 lip 08:08
iwo: To nie zadanie z tego roku
17 lip 08:09
Mariusz:
Iwo masz jakiś pomysł na to aby pokazać że kąty ∡DCB oraz ∡DAC mają tę samą miarę ?
17 lip 09:10
iwo: Nie mam pomysłu
17 lip 10:43
Mariusz:
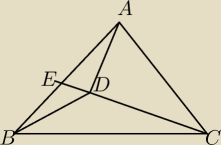
Trochę rysunek mi się nie udał ale chyba wiadomo o co chodzi
Gdyby udało się pokazać że AE = EC to otrzymamy miarę kąta x
z sumy miar kątów w trójkącie ABC
Kiedy trójkąty są równoramienne ?
1. Miary kątów przy podstawie są równe
2. Długości co najmniej dwóch boków są równe
3. Jeżeli jeden z wierzchołków trójkąta jest środkiem pewnego okręgu
a pozostałe dwa wierzchołki leżą na tym okręgu
1. Odpada bo to chcemy pokazać wiedząc że trójkąt jest równoramienny
Co do 2. to AE musiałoby być równe EC
Jeśli chodzi o 3. to E byłby środkiem pewnego okręgu a A oraz C leżałyby na tym okręgu
17 lip 12:45
Mila:
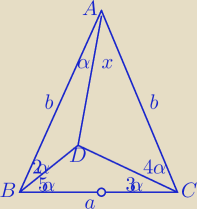
Nie napisałeś całej treści. To test wyboru.
Możemy wykluczyć błędne odpowiedzi albo znaleźć prawidłową odpowiedź rozwiązując.
1)
Gdyby Δ był prostokątny to nie ma w dystraktorach pasującej odpowiedzi .(sprawdź)
2) Jeśli a<b jak na rysunku:
15α<180
o
α<12
o
x=180−15α
180−15α<90
α>6
o
odp. α=10
o
17 lip 17:06
kangur:
Jeśli 6
o < α < 12
o to pasuje także odpowiedź C, to jest 9
o.

17 lip 20:24
Mariusz:
Lepiej to pokazać rozwiązując to zadanie
Po pokazaniu że kąty ∡DCB oraz ∡DAC mają tę samą miarę
łatwo policzyć α
17 lip 20:35
Mila:
Rzeczywiście, umknęła mi ta 9, potrzebne jeszcze jedno ograniczenie albo jakieś sprawdzenie.
Dziękuję.

Wymyśliłeś co to ma być? Czy mam dalej nad tym pomyśleć?
17 lip 20:42
iwo: Jeszcze nie mam rozwiązania
17 lip 22:18
Bogdan:
Dobry wieczór
 ite
ite wczoraj przed północą zamieściła równanie: sin(α) + sin(5α) = sin(11α), można je
uzyskać korzystając z twierdzenia sinusów.
sin(11α)−sin(α) = 2sin(5α)cos(6α), zatem:
| | 1 | |
sin(11α)−sin(α)−sin(5α)=0 ⇒ 2sin(5α)cos(6α)−sin(5α)=0 ⇒ 2sin(5α)*(cos(6α)− |
| )=0 |
| | 2 | |
| | 1 | |
sin(5α) = 0 lub cos(6α) = |
| = cos60o, ostatecznie α = 10o |
| | 2 | |
17 lip 23:06
"młody":
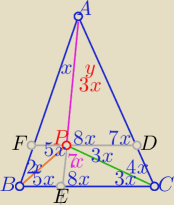
18x=180
o
x=10
o
======
17 lip 23:10
Mariusz:
Bogdan z twierdzenia sinusów ?
Domyśliłem się tego ale jak je ułożyć
18 lip 05:40
Mariusz:
Ja z twierdzenia sinusów otrzymałem takie równanie
cos(α)−cos(7α)−cos(9α)+cos(13α)=0
18 lip 06:02
Bogdan:
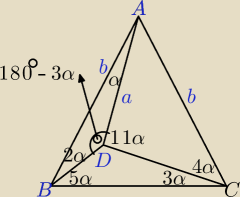
|∡ADB| = 180
o − 3α, sin(180
o − 3α) = sin(3α)
|∡BDC| = 180
o − 8α, |∡ADC| = 360
o − (180
o − 3α) − (180
o − 8α) = 11α
Skorzystamy z: sin(4α) = 2sin(2α)cos(2α) oraz 2sin(3α)cos(2α) = sin(5α) + sin(α)
Z twierdzenia sinusów:
| | b | | a | | a*sin(3α) | |
w ΔABD: |
| = |
| ⇒ b = |
| |
| | sin(3α) | | sin(2α) | | sin(2α) | |
| | b | | a | |
w ΔACD: |
| = |
| ⇒ b*2sin(2α)cos(2α) = a*sin(11α) |
| | sin(11α) | | sin(4α) | |
| a*sin(3α) | |
| *2sin(2α)cos(2α) = a*sin(11α) ⇒ 2sin(3α)cos(2α) = sin(11α) |
| sin(2α) | |
sin(5α) + sin(α) = sin(11α)
18 lip 08:02
iwo: Czemu u "młodego" EPC=7x?
18 lip 08:15
ite:
Bogdan dziękuję 23:06

18 lip 10:57
iwo: I skąd 8x na rysunku?
18 lip 14:42
Mariusz:
No to ja użyłem twierdzenia sinusów w ten sposób
W ΔABD
| AB | | AD | |
| = |
| |
| sin(180−3α) | | sin(2α) | |
W ΔADC
| sin(2α) | | sin(4α) | |
| = |
| |
| sin(3α) | | sin(11α) | |
sin(2α)sin(11α)=sin(3α)sin(4α)
2sin(2α)sin(11α)=2sin(3α)sin(4α)
cos(9α)−cos(13α)=cos(α)−cos(7α)
cos(α)−cos(7α)−cos(9α)+cos(13α)=0
Wyprowadźmy rekurencyjny wzór na wielomiany Czebyszowa
cos((m+1)t) = cos(t)cos(mt) − sin(t)sin(mt)
cos((m−1)t) = cos(t)cos(mt) + sin(t)sin(mt)
cos((m+1)t) + cos((m−1)t) = 2cos(t)cos(mt)
T
m+1(x) + T
m−1(x) = 2xT
m
T
m+1(x) = 2xT
m − T
m−1(x)
Niech n = m−1
T
n+2(x) = 2xT
n+1 − T
n(x)
T
1(x) = x
T
0(x) = 1
T
2(x)=2x
2 − 1
T
3(x)=2x(2x
2 − 1)−x
T
3(x)=4x
3−3x
T
4(x)=2x(4x
3−3x)−(2x
2 − 1)
T
4(x)=8x
4−8x
2+1
T
5(x)=2x(8x
4−8x
2+1)−(4x
3−3x)
T
5(x)=16x
5−20x
3+5x
T
6(x)=2x(16x
5−20x
3+5x)−(8x
4−8x
2+1)
T
6(x)=32x
6−40x
4+10x
2−8x
4+8x
2−1
T
6(x)=32x
6−48x
4+18x
2−1
T
7(x)=2x(32x
6−48x
4+18x
2−1)−(16x
5−20x
3+5x)
T
7(x)=(64x
7−96x
5+36x
3−2x)−(16x
5−20x
3+5x)
T
7(x)=64x
7−112x
5+56x
3−7x
T
8(x)=2x(64x
7−112x
5+56x
3−7x)−(32x
6−48x
4+18x
2−1)
T
8(x)=(128x
8−224x
6+112x
4−14x
2)−(32x
6−48x
4+18x
2−1)
T
8(x)=128x
8−256x
6+160x
4−32x
2+1
T
9(x)=2x(128x
8−256x
6+160x
4−32x
2+1)−(64x
7−112x
5+56x
3−7x)
T
9(x)=(256x
9−512x
7+320x
5−64x
3+2x)−(64x
7−112x
5+56x
3−7x)
T
9(x)=256x
9−576x
7+432x
5−120x
3+9x
T
10(x)=2x(256x
9−576x
7+432x
5−120x
3+9x)−(128x
8−256x
6+160x
4−32x
2+1)
T
10(x)=(512x
10−1152x
8+864x
6−240x
4+18x)−(128x
8−256x
6+160x
4−32x
2+1)
T
10(x)=512x
10−1280x
8+1120x
6−400x
4+50x
2−1
T
11(x)=2x(512x
10−1280x
8+1120x
6−400x
4+50x
2−1)
−(256x
9−576x
7+432x
5−120x
3+9x)
T
11(x)=(1024x
11−2560x
9+2240x
7−800x
5+100x
3−2x)−(256x
9−576x
7+432x
5−120x
3+9x)
T
11(x)=1024x
11−2816x
9+2816x
7−1232x
5+220x
3−11x
T
12(x)=2x(1024x
11−2816x
9+2816x
7−1232x
5+220x
3−11x)−
(512x
10−1280x
8+1120x
6−400x
4+50x
2−1)
T
12(x)=2048x
12−5632x
10+5632x
8−2464x
6+440x
4−22x
2)−
(512x
10−1280x
8+1120x
6−400x
4+50x
2−1)
T
12(x)=2048x
12−6144x
10+6912x
8−3584x
6+840x
4−72x
2+1
T
13(x)=2x(2048x
12−6144x
10+6912x
8−3584x
6+840x
4−72x
2+1)−
(1024x
11−2816x
9+2816x
7−1232x
5+220x
3−11x)
T
13(x)=(4096x
13−12288x
11+13824x
9−7168x
7+1680x
5−144x
3+2x)−
(1024x
11−2816x
9+2816x
7−1232x
5+220x
3−11x)
T
13(x) = 4096x
13 − 13312x
11+16640x
9−9984x
7+2912x
5−364x
3+13x
Teraz można zauważyć że wielomiany Czebyszowa są parzyste dla parzystego n
a nieparzyste dla nieparzystego n
W sumie którą otrzymałem były nieparzyste wielokrotności cosinusów więc otrzymamy
równanie wielomianowe 13. stopnia które łatwo sprowadzić do równania 6. stopnia
cos(13α)−cos(9α)−cos(7α)+cos(α)=0
(4096x
13 − 13312x
11+16640x
9−9984x
7+2912x
5−364x
3+13x)−
(256x
9−576x
7+432x
5−120x
3+9x)−(64x
7−112x
5+56x
3−7x)+x = 0
1024x
13−3328x
11+4096x
9−2368x
7+648x
5−75x
3+3x = 0
x(1024x
12−3328x
10+4096x
8−2368x
6+648x
4−75x
2+3)=0
Niech t=x
2
Mamy do rozwiązania równanie wielomianowe
1024t
6−3328t
5+4096t
4−2368t
3+648t
2−75t+3=0
Stopień równania można jeszcze obniżyć znajdując całkowity pierwiastek
1024 −3328 4096 −2368 648 −75 3
1 1024 −2304 1792 −576 72 −3 0
1024t
6−3328t
5+4096t
4−2368t
3+648t
2−75t+3=
(t−1)(1024t
5 −2304t
4 + 1792t
3 −576t
2 + 72t −3)
Wielomian 1024t
5 −2304t
4 + 1792t
3 −576t
2 + 72t −3
podzieli się bez reszty przez trójmian kwadratowy 16t
2−12t+1
64t
3−96t
2+36t−3
1024t
5 −2304t
4 + 1792t
3 −576t
2 + 72t −3 : 16t
2−12t+1
− (1024t
5 − 768t
4+64t
3 )
−1536t
4+1728t
3−576t
2
−(−1536t
4+1152t
3−96t
2)
576t
3−480t
2+72t
−(576t
3−432t
2+36t)
−48t
2+36t−3
−(−48t
2+36t−3)
0
Mamy zatem
1024t
6−3328t
5+4096t
4−2368t
3+648t
2−75t+3=
(t−1)(16t
2−12t+1)(64t
3−96t
2+36t−3)
a stąd już można otrzymać szukaną wartość
18 lip 17:10
M:

18 lip 17:41
Mila:
1)
Iwo, wystarczy sprawdzić równanie ite.
α=10o spełnia równanie sin(5α) + sin(α) = sin(11α)
x=9o nie spełnia.
2)
Ad 23:10
kąt AEC=8x jako kąt zewnętrzny ΔABE
Kąt EPC=7x ( to prawda) − nie wiem jak to 'młody " wyjaśnia?
18 lip 18:41
kangur:
Mariuszu, nie strzela się do muchy z armaty

18 lip 19:46
Mila:
Iwo, zaglądaj tutaj, znajdę czas to może uda mi się podać w miarę proste rozwiązanie
bez wspomagania trygonometrią

Na razie mam skomplikowane.
19 lip 00:08
Mariusz:
To "wspomagane trygonometrią" rozwiązanie pokazane przez Bogdana jest całkiem niezłe
i nawet krótkie
Co do twierdzenia sinusów to jak się nie wybierze odpowiednich par boków i kątów to
wtedy można sobie liczyć tak jak to pokazałem 18 lip 2022 17:10
19 lip 12:58
Mariusz:
Iwo możesz zaglądać Mila w przeciwieństwie do Maciessów i innych jak obieca to odpowie
19 lip 13:00
iwo: ok
19 lip 14:31
ite:
w tak życzliwej atmosferze rozwiązywanie zadań jest przyjemnością
19 lip 15:55
Mila:
ite trygonometrycznie rozwiązałam, korzystając z tw. Cevy w wersji trygonometrycznej.
To mi się nasunęło , bo ładnie zaznaczono kąty pod to tw.
Jeśli chcesz to napiszę.
Myślę, że jest proste rozwiązanie, ale "coś" trzeba zauważyć.
Geometrycznie zauważyłam wiele własności− to ciekawy trójkąt z tak zaznaczonymi kątami,
ale jednej informacji nie widzę na moich bohomazach rysunkowych.
Uruchomiłam przetwory i pilnuję , aby nie było katastrofy w kuchni.
Kiedyś wybuchły mi jajka na sufit i mąż musiał go umyć i wymalować.
Pozdrawiam.

19 lip 18:21
ite:
Przetwory, które wybuchły to nie jest jeszcze to najgorsze. Łatwiej schodzą z sufitu niż
bateria potraktowana jak akumulator i nastawiona do naładowania.
Oczywiście wpisz rozwiązanie z twierdzeniem Cevy, zaglądają tu osoby przygotowujące się do
konkursów, to takie nieszkolne twierdzenie się im przyda.
A ja w nowym wątku dodam zadanie z kątami, które przez kilka dni atakowałam bezskutecznie.
19 lip 21:40
Mila:
Niezbyt precyzyjnie napisałam, że rozwiązałam. Po prostu wg tw. Cevy sprawdziłam dla x=10o
i to poszło łatwo. Jeśli Iwo wyrazi chęć zobaczenia to napiszę.
Gdyby było zadanie otwarte, to równanie nie było łatwe.
Łatwiej było z tw. sinusów.
Mam rozwiązanie ale obawiam się pytań, jak to było z jednym zadaniem, chyba pamiętasz.
19 lip 22:15
Mila:
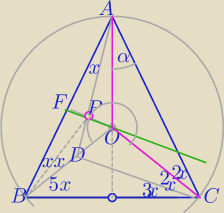
1)
BP− dwusieczna kąta ABD
ΔBPA− Δrównoramienny
FP⊥AB i F− jest środkiem AB⇒
prosta FP jest symetralną AB
AE− symetralna BC
Punkt O − środek okręgu opisanego na ΔABC
2)∡AOC=2*7x=14x
ΔAOC≡ΔAOB− Δrównoramienne
α=2x
3) w ΔABC
∡A=4x
2*7x+4x=180
o
x=10
o
=============
19 lip 22:40
iwo: Mila dzięki ale nie wpadłbym na tak skomplikowany sposób niestety
19 lip 23:12
Mila:
A rozwiązanie z zastosowaniem tw. sinusów ?
19 lip 23:41
iwo: Tak z sinusami jednak łatwiejsze.
20 lip 08:06
Mariusz:
Jedyny problem z twierdzeniem sinusów to wybrać odpowiednie pary (boków i kątów)
Porównajcie mój wpis i wpisy Bogdana
Pomyślałem o okręgu w celu pokazania że ΔACE jest równoramienny
gdzie E jest przecięciem odcinka AB i przedłużenia odcinka CD
ale Mila lepiej wykorzystała pomysł z okręgiem
20 lip 11:15
an: Milu czy możesz podać na jakiej podstawie można stwierdzić, że punkt O będący środkiem okręgu
należy do trójkątów oznaczonych jako AOB oraz AOC.
20 lip 15:59
Mila:
To właśnie mnie niepokoi. !
ΔABC− Δrównoramienny
O− środek okręgu opisanego na tym Δ.
Po przedłużeniu BO i CO do przecięcia z AB i AC spełnione jest tw. Cevy zatem proste AO, CO, BO
przecinają się w punkcie O.
Sprawdziłam z trygonometrycznej wersji tw. Cevy i też się zgadza. Czy to wystarczy?
W każdej mojej wersji ( nie napisanej tutaj) mam lukę.
Myślałam jeszcze nad innym uzasadnieniem, ale też mam wątpliwości.
Problem otwarty.
Masz rozwiązanie bez trygonometrii?
To co "młody " podał też jest prawdą, ale nie widzę dlaczego ma być kąt (7x ) w ΔEPC.
Mogę Ci podać linka do teorii ( po angielsku) ws syntetycznych metod w geometrii, jeśli nie
masz.
20 lip 18:20
an: Ja nie zgłaszam wątpliwości, że w tych zadaniach to się zgadza z prawidłowym wynikiem,
jednak moim zdaniem takiego rozwiązania nie można uznać, rzucę też kamieniem w siebie
co do mojego rozwiązania forum/413795.html z 29.05 podobna sprawa.
20 lip 21:19
iwo: A czy można jakoś wykazać ze BD przechodzi przez O?
20 lip 21:52
Mila:
Na razie pozostaje prawidłowe rozwiązanie z zastosowaniem tw. sinusów. [B [Ite i Bogdan]].
20 lip 23:00
Mila:
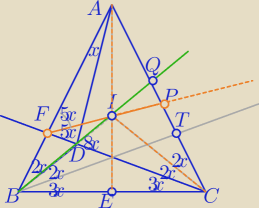 Iwo
Iwo, bez wątpliwości możesz skorzystać z tego, że punkt I jest środkiem okręgu
wpisanego w ΔAFC.
Zaznaczyłam miary tylko kilku kątów oprócz danych w treści.
Działaj.

22 lip 16:25
iwo: No tak, a czemu AFC=10x i IDC=8x?
22 lip 17:37
Mila:
∡AFC=10x jako kąt zewnętrzny ΔFBC ( suma 2kątów wew. nieprzyległych do niego − 7x+3x))
∡IDC=8x − jako kąt zewnętrzny Δ DBC (5x+3x)
22 lip 17:54
iwo: Ok ale niestety nadal nie widzę jak to wykorzystać

22 lip 18:35
Mila:
Wyznacz miary kątów przy T,P, Q w podobny sposób.
22 lip 18:45
iwo: Mam T=10x, P=9x, Q=12x , tyle tych trójkątów i czworokątów że nadal nie wiem
22 lip 20:22
Mila:
Dotąd dobrze. Dalej:
∡QIP=3x
∡PIC=7x
K punkt na prostej FP, po prawej od punktu P
∡KPC=180−9x⇒∡FPC=9x
dalej sam
22 lip 20:50
iwo: Skąd PIC=7x i KPC=180−9x ?
22 lip 21:27
Mila:
∡IPQ=9x to 2x+7x da kąt zewnętrzny 9x.
22 lip 21:33
iwo: Nadal nie wiem czemu PIC=7x
22 lip 21:59
iwo: Ok Kat PIC już wiem
A KPC=180−9x?
22 lip 22:03
iwo: K to przecięcie AD z FP?
22 lip 22:05
Mila:
Nie, to ma być półprosta PK , K na prawo od P.
Może jutro narysuję.
22 lip 22:14
iwo: Ok mimo że mam teraz po prawej stronie to też nie wiem czemu KPC=180−9x?
22 lip 22:23
iwo: KPC=IPQ czy nie?
22 lip 22:27
Mila:
Wszystkie 4 kąty wokół P są równe.
22 lip 22:37
iwo: Jeśli wszystkie wokół P są równe to by było po zadaniu.
22 lip 23:07
Mila:
Tak.
22 lip 23:20
iwo: Tylko problem w tym jak to pokazać
22 lip 23:25

 Trochę rysunek mi się nie udał ale chyba wiadomo o co chodzi
Gdyby udało się pokazać że AE = EC to otrzymamy miarę kąta x
z sumy miar kątów w trójkącie ABC
Kiedy trójkąty są równoramienne ?
1. Miary kątów przy podstawie są równe
2. Długości co najmniej dwóch boków są równe
3. Jeżeli jeden z wierzchołków trójkąta jest środkiem pewnego okręgu
a pozostałe dwa wierzchołki leżą na tym okręgu
1. Odpada bo to chcemy pokazać wiedząc że trójkąt jest równoramienny
Co do 2. to AE musiałoby być równe EC
Jeśli chodzi o 3. to E byłby środkiem pewnego okręgu a A oraz C leżałyby na tym okręgu
Trochę rysunek mi się nie udał ale chyba wiadomo o co chodzi
Gdyby udało się pokazać że AE = EC to otrzymamy miarę kąta x
z sumy miar kątów w trójkącie ABC
Kiedy trójkąty są równoramienne ?
1. Miary kątów przy podstawie są równe
2. Długości co najmniej dwóch boków są równe
3. Jeżeli jeden z wierzchołków trójkąta jest środkiem pewnego okręgu
a pozostałe dwa wierzchołki leżą na tym okręgu
1. Odpada bo to chcemy pokazać wiedząc że trójkąt jest równoramienny
Co do 2. to AE musiałoby być równe EC
Jeśli chodzi o 3. to E byłby środkiem pewnego okręgu a A oraz C leżałyby na tym okręgu
 Nie napisałeś całej treści. To test wyboru.
Możemy wykluczyć błędne odpowiedzi albo znaleźć prawidłową odpowiedź rozwiązując.
1)
Gdyby Δ był prostokątny to nie ma w dystraktorach pasującej odpowiedzi .(sprawdź)
2) Jeśli a<b jak na rysunku:
15α<180o
α<12o
x=180−15α
180−15α<90
α>6o
odp. α=10o
Nie napisałeś całej treści. To test wyboru.
Możemy wykluczyć błędne odpowiedzi albo znaleźć prawidłową odpowiedź rozwiązując.
1)
Gdyby Δ był prostokątny to nie ma w dystraktorach pasującej odpowiedzi .(sprawdź)
2) Jeśli a<b jak na rysunku:
15α<180o
α<12o
x=180−15α
180−15α<90
α>6o
odp. α=10o

 Wymyśliłeś co to ma być? Czy mam dalej nad tym pomyśleć?
Wymyśliłeś co to ma być? Czy mam dalej nad tym pomyśleć?
 ite wczoraj przed północą zamieściła równanie: sin(α) + sin(5α) = sin(11α), można je
uzyskać korzystając z twierdzenia sinusów.
sin(11α)−sin(α) = 2sin(5α)cos(6α), zatem:
ite wczoraj przed północą zamieściła równanie: sin(α) + sin(5α) = sin(11α), można je
uzyskać korzystając z twierdzenia sinusów.
sin(11α)−sin(α) = 2sin(5α)cos(6α), zatem:
 18x=180o
x=10o
======
18x=180o
x=10o
======
 |∡ADB| = 180o − 3α, sin(180o − 3α) = sin(3α)
|∡BDC| = 180o − 8α, |∡ADC| = 360o − (180o − 3α) − (180o − 8α) = 11α
Skorzystamy z: sin(4α) = 2sin(2α)cos(2α) oraz 2sin(3α)cos(2α) = sin(5α) + sin(α)
Z twierdzenia sinusów:
|∡ADB| = 180o − 3α, sin(180o − 3α) = sin(3α)
|∡BDC| = 180o − 8α, |∡ADC| = 360o − (180o − 3α) − (180o − 8α) = 11α
Skorzystamy z: sin(4α) = 2sin(2α)cos(2α) oraz 2sin(3α)cos(2α) = sin(5α) + sin(α)
Z twierdzenia sinusów:



 Na razie mam skomplikowane.
Na razie mam skomplikowane.

 1)
BP− dwusieczna kąta ABD
ΔBPA− Δrównoramienny
FP⊥AB i F− jest środkiem AB⇒
prosta FP jest symetralną AB
AE− symetralna BC
Punkt O − środek okręgu opisanego na ΔABC
2)∡AOC=2*7x=14x
ΔAOC≡ΔAOB− Δrównoramienne
α=2x
3) w ΔABC
∡A=4x
2*7x+4x=180o
x=10o
=============
1)
BP− dwusieczna kąta ABD
ΔBPA− Δrównoramienny
FP⊥AB i F− jest środkiem AB⇒
prosta FP jest symetralną AB
AE− symetralna BC
Punkt O − środek okręgu opisanego na ΔABC
2)∡AOC=2*7x=14x
ΔAOC≡ΔAOB− Δrównoramienne
α=2x
3) w ΔABC
∡A=4x
2*7x+4x=180o
x=10o
=============
 Iwo, bez wątpliwości możesz skorzystać z tego, że punkt I jest środkiem okręgu
wpisanego w ΔAFC.
Zaznaczyłam miary tylko kilku kątów oprócz danych w treści.
Działaj.
Iwo, bez wątpliwości możesz skorzystać z tego, że punkt I jest środkiem okręgu
wpisanego w ΔAFC.
Zaznaczyłam miary tylko kilku kątów oprócz danych w treści.
Działaj.
