Równanie okręgu vol: Napisz równanie okręgu przechodzącego przez punkt A (0, −1) który jest jednocześnie styczny do prostych k: y=0 oraz l: 4x− y +22 Zapisałem taki układ równań k{r=U{ |4x_s − 3y_s + 22| }{ √16+9 &(0 − x_s)² + (−1 − y_s)² = r² &r²=y² i wychodzą mi dziwne liczby niezgodne z odpowiedziami. Proszę o pomoc.

vol: cos się schrzanilo : c prosta l: 4x − 3y +22 = 0

Mila: l: 4x − 3y +22 = 0 3y=4x+22

	4		22
y=		x+
	3		3

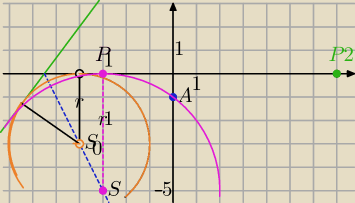
S=(a,b)− wsp. środka okręgu Punkty styczności: P=(a,0)− na osi OX Na rysunku pomarańczowy okrąg to jeden z okręgów stycznych do prostych k i l Środek okręgu stycznego do OX i prostej l leży na dwusiecznej kąta między k i l i przechodzi przez punkt A. S=(a,−r), A=(0,−1) ∊okręgu, r>0 (0−a)²+(−1+r)²=r² a²+1−2r+r²=r² a²+1=2r odległość S od punktów styczności:

	|4a+3r+22|
r=
	5

5r=|4a+3r+22| 5r=4a+3r+22 lub 5r=−4a−3r−22 2r=4a+22 lub 8r=−4a −22 a²+1=4a+22 lub a²+1=−a−11/2 (Δ<0) a²−4a−21=0 , Δ=100, a=−3 lub a=7 a=−3 r=5 S=(−3,−5) (x+3)²+(y+5)²=25 lub a=7,r=25 S=(7,−25) (x−7)²+(y+25)²=625 ten okrąg nie zmieści się na tym rysunku

Eta: https://matematykaszkolna.pl/forum/385536.html