. sylwiaczek: napisz rownanie okregu przechodzacego przez punkt A(0,−1) ktory jest jednoczesnie styczny do prostych k: y=0 i l: 4x−3y+22=0

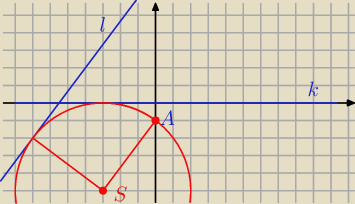
Janek191: S = ( − 3, − 5) r = 5 ( x + 3)² ( y + 5)² = 25

Janek191: ( x + 3)² + ( y + 5)² = 25

sylwiaczek: skad wyznaczyles srodek i promien?

M: Czy mógłby ktoś to wytłumaczyć?

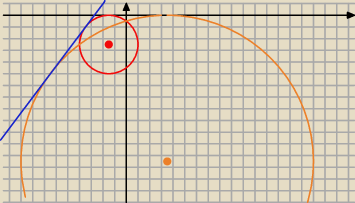
a@b: Są dwa takie okręgi : o₁: ( x+3)²+(y+5)²=25 o₂: (x−7)²+(y+25)²=625

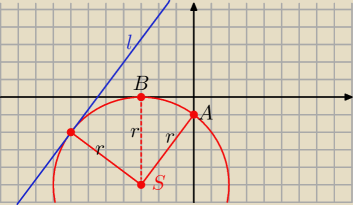
a@b: B(a,0) S(a,b) , |b|=r i A(0,−1) b²=r²=|SA|²= a²+(b+1)² ⇒ a²+b²+2b+1=b² ⇒ b=−(a²+1)/2 S(a, −(a²+1)/2)

	| 4*a+3(a2+1)/2+(22)|
d=|SC|=r i l : 4x−3y+22=0 ⇒		= |b|= (a2+1)/2
	√14+9

8a+3a²+3+44=5a²+5 a²−4a−21=0 i S(a,b) , r=|b| .................. ................ dokończ

salamandra: Mógłby mi ktoś podpowiedzieć co krok po kroku należy tu zrobić? Muszę przerobić dużo zadań z okręgami, bo kuleję nad nimi. Podstawowe moje pytanie − jak wykorzystać informację, że okrąg jest styczny do osi x? Na razie obliczyłem |SA| i mam a²+1+2b+b² i nie wiem co dalej z tym zrobić.

Jerzy: Rzędna środka jest równa promieniowi.

salamandra: czyli b = r? dla S(a,b)

a@b: Wszystko wyjaśniłam wyżej Nie wiem czego jeszcze nie rozumiesz?

a@b: r=|b|

salamandra: Zazwyczaj bardziej rozumiem jeśli są jakieś komentarze do rozwiązania, z samego rozwiązania czasami ciężko mi wszystko wywnioskować. Na ten moment na przykład nie wiem, czemu z d, nagle zrobiła się |b|, (wiem skąd b, ale nie wiem skąd ten moduł) Ja zapisałem to tak:

	|4a+3a2+32+22|
d=r=b =		/ *5
	5

	3a2+3
|4a+		+22| = b
	2

	3a2+3		3a2+3
4a+		+22 = b v 4a+		+22 = −b
	2		2

	−a2−1
no i za b wstawiam		− też dobrze?
	2

Jerzy: 14:00 tak.

Jerzy: Ściślej: |b| = r , jak 14:15

salamandra: Czyli mój zapis jest również poprawny?

salamandra: Wyszedł mi zbiór pusty, czyli coś jest nie tak

salamandra: Ok, błąd jest w tym, że faktycznie powinienem użyć |b|, ale mimo to, mam:

	−a2−1
|4a+3a2+32+22| = 5*|		|
	2

I nie wiem jak rozbić te wartości bezwzględne, bo skąd wiem, że jak jedna będzie dodatnia, to druga nie będzie ujemna?