
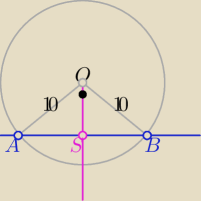
 PABO=50 ⇒R=10
AB: x−7y+40=0 wektor SO ⊥ do AB i |AS|=|SO|=5√2
→ →
to SO =[1,−7] lub [−1,7] ⇒ SO= [ x+5, y−5]
x+5=1 ∧ y−5=−7 v x+5= −1 ∧ y−5=7
x= −4 ∧ y=−2 v x= −6 ∧ y= 12
O=(−4,−2) v O=(−6,12)
o: (x+4)2+(y+2)2=100 lub o:( x+6)2+(y−12)2=100
========================================
→ →
AS ⊥OS i |AS|=|OS|=5√2
→
AS= [x+5, y−5] =[ 7,1] lub [−7,−1]
x+5=7 ∧ y−5=1 lub x+5= −7 ∧ y−5= −1
x= 2 ∧ y= 6 lub x= −12 ∧ y= 4
A=(2,6) B=(−12,4)
======================
PABO=50 ⇒R=10
AB: x−7y+40=0 wektor SO ⊥ do AB i |AS|=|SO|=5√2
→ →
to SO =[1,−7] lub [−1,7] ⇒ SO= [ x+5, y−5]
x+5=1 ∧ y−5=−7 v x+5= −1 ∧ y−5=7
x= −4 ∧ y=−2 v x= −6 ∧ y= 12
O=(−4,−2) v O=(−6,12)
o: (x+4)2+(y+2)2=100 lub o:( x+6)2+(y−12)2=100
========================================
→ →
AS ⊥OS i |AS|=|OS|=5√2
→
AS= [x+5, y−5] =[ 7,1] lub [−7,−1]
x+5=7 ∧ y−5=1 lub x+5= −7 ∧ y−5= −1
x= 2 ∧ y= 6 lub x= −12 ∧ y= 4
A=(2,6) B=(−12,4)
======================
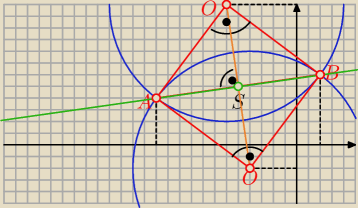 I wszystko gra
I wszystko gra  jak na rys.
jak na rys.
