Stosunek dlugosci w rownolegloboku Kaczapuri: Stosunek długości przekątnych równoległoboku wynosi √⁴³₅₇. Oblicz stosunekdługości dłuższego boku do krótszego boku tego równoległoboku wiedząc, że suma sinusów wszystkich kątów wewnętrznych równoległoboku jest równa 2√3

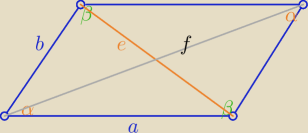
kotek: sinα= sinβ to 4sinα=2√3 ⇒ ..... α=60^o , β=120^o

	e2		34		43
(*) f2+e2=2(a2+b) i z treści zad.		=		⇒ f2=		e2
	f2		57		57

100f²=2*57(a²+b²) ⇒ 50f²=57a²+57b² z tw. cosinusów f²= a²+b²+ab to 50a²+50b²+50ab=57a²+57b² 7a²+7b²=50ab \ :ab >0

	a		b		50
		+		=
	b		a		7

a
	=t >0
b

7t²−50t+7=0 ........................ dokończ

a
	=t=..........
b

Kaczapuri: Wszystko rozumiem tylko dlaczego sinα= sinβ? @kotek

kotek: α+β=180^o ⇒ β= 180^o−α to sinβ= sin(180^o−α)=sinα jasne?

Kaczapuri: tak dziekuje @kotek

Kaczapuri: @kotek jeszcze jedno pytanie, skad sie wzielo f²+e²=2(a²+b)?

kotek: W każdym równoległoboku z tw. cosinusów e²=a²+b²−2ab*cosα i f²=a²+b²+2abcosα bo cosβ= −cosα + −−−−−−−−−−−−−− e²+f²= 2a²+2b² ==============

kotek: Zamurowało Cię ?