oblicz całkę nieoznaczoną zbiorek: Prosiłbym o pomoc w wyprowadzeniu wzoru rekurencyjnego dla całki nieoznaczonej. ∫1/(1+x²)ⁿ dx

Mila: Patrz Krysicki, jest wyprowadzona.

Mila: Na youtube: https://www.youtube.com/watch?v=HX_hX8Jy0ag

zbiorek: o dzięki wielkie

Mariusz: Co do tego gościa z youtube to oglądam go czasem On w swoim video ma całkę oznaczoną do policzenia ale mimo to wyprowadza wzór rekurencyjny także dla całki nieoznaczonej

Mila: Mariusz, ja na youtube oglądam często różne filmiki matematyczne, w różnych językach. Hindusi są niesamowici. Wprawdzie nie znam języka, ale wszystko jest klarownie rozpisane. Ciekawe są też filmiki z planimetrii po hiszpańsku i włosku (chyba). Uczyłam się łaciny więc wiele określeń kojarzę i szybko zapamiętuję. Ponadto jest ładnie przedstawione. Rosyjskie filmiki są różne, to rozumiem doskonale. Niektóre zadania my na forum prościej rozwiązujemy, ale stereometria pięknie wytłumaczona, a szczególnie przekroje brył. Zastosowanie tw. Menelausa − dużo przykładów.

chichi: Polecam jego materiały z teorii liczb, ma facet smykałkę do tego

chichi: "Niektóre zadania my na forum prościej rozwiązujemy, ale stereometria pięknie wytłumaczona, a szczególnie przekroje brył." Masz na myśli, że ta stereometria pięknie wytłumaczona tu na forum, czy na YouTube?

Mila: Nie odniosłam się do prezentacji zadań ze stereometrii na forum lecz na youtube i to do tego co oglądałam. Oglądałam część prezentacji rosyjskiego autora. Materiały z teorii liczb też oglądam.

chichi: Rozumiem, czy mogłabyś podlinkować te materiały do stereometrii?

Mila: Jeśli znajdę to tak

Mila: Będę szukać , math24.biz jest, ale tej stereometrii nie mogę znaleźć.

Mariusz: Ja jak chodziłem do szkoły średniej i miałem całki to ten wzorek samodzielnie wyprowadziłem Co do hiszpańskiego to mam u siebie podręcznik Oskara Perlina i książkę do gramatyki jego syna ale to jest dobre na początek przygody z tym językiem Zdążyłem jednak zauważyć pewne podobieństwo choć łaciny nie znam (kilka słów i zwrotów na krzyż) Na pierwszy rzut oka mogłoby się wydawać że to włoski powinien być podobny do łaciny Chichi ty się bawisz geometrią , mógłbyś zajrzeć jeszcze raz do tematu Szkolniaka w którym opisałem konstrukcyjny sposób napisania równania dwusiecznej tyle że wychodzą dwie wzajemne prostopadłe proste i która z nich dzieli kąt wewnętrzny trójkąta Skrobnąłem programik do znajdowania równań dwusiecznych w Pascalu i chciałbym uporządkować te równania prostych co otrzymuję na wyjściu ale aby to zrobić muszę wiedzieć która dwusieczna dzieli kąt wewnętrzny trójkąta Iloczyn skalarny daje wartość cosinusa przeskalowaną o długości wektorów Pole rownoległoboku daje wartość sinusa przeskalowaną o długości wektorów ale czy to można by wykorzystać

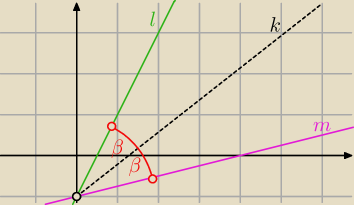
chichi: l < k < m

chichi: m < k < l **

chichi: Aby dwie proste wyznaczyły nam kąt, muszą być nierównoległe, zatem ich współczynniki muszą być różne. Mając równania tych prostych, możemy znaleźć punkt przecięcia się tych prostych − punkt z którego wychodzą ramiona kąta (przez niego przechodzi również szukana dwusieczna, a następnie ograniczyć tę dwusieczną prostymi, które wyznaczają ramiona kąta, którego dwusiecznej szukamy. Natomiast to wypada jeszcze rozpatrywania mnóstwa przypadków, które determinują wzajemne położenia tych prostych w układzie

Mariusz: Chichi czytałeś coś o otoczce wypukłej ? W oryginalnym algorytmie Grahama było sortowanie punktów po współrzędnych biegunowych (Sortowane tam były kąty , przy czym ze względów numerycznych liczyło się wartości pól równoległoboków a dla punktów współliniowych sortowane były odległości punktów od punktu o maksymalnej współrzędnej x, tutaj też ze względów numerycznych nie liczyło się pierwiastków) Może dałoby się to wykorzystać i tutaj Komputerowi trzeba jasno napisać w jaki sposób ma wybrać tę dwusieczną inaczej polecenia nie wykona

chichi: Szczerze, to pierwszy raz słyszę ten termin, musiałbym poczytać

Mariusz: Chichi na ważniaku mają to https://wazniak.mimuw.edu.pl/index.php?title=Zaawansowane_algorytmy_i_struktury_danych/Wyk%C5%82ad_11 Ale mi głównie chodzi o to czy sposób porządkowania punktów po współrzędnych biegunowych występujący w algorytmie Grahama można wykorzystać do uporządkowania tych dwóch prostych aby łatwo można było wybrać tę prostą w której zawiera się dwusieczna która dzieli kąt wewnętrzny trójkąta Samo znajdowanie równań dwusiecznych już oprogramowałem i zdaje się że uwzględniłem przypadki takie jak dzielenie przez zero itp

Mariusz: Chichi co do wyboru tej dwusiecznej to już wcześniej w tablicach znalazłem wzór na tangens kąta między prostymi a na youtube znalazłem jak go wykorzystać i program do znajdowania równania okręgu wpisanego w trójkąt powinien działać (Przydałoby się jeszcze przetestować wszystkie możliwe przypadki np możliwe dzielenie przez zero , pierwiastka z liczby ujemnej raczej nie będzie bo pod pierwiastkiem mamy sumę kwadratów)

chichi: Tak, znam ten wzór. Używa się go w liceum. A dlaczego zależy Ci tak na napisaniu tego programu?

Mariusz: Ten pomysł od kolesi z youtube na tangens się raczej nie sprawdził ale myślę że mój pierwszy pomysł z porządkowaniem kątów jak w algorytmie Grahama dla otoczki wypukłej by zadziałał Niech wierzchołek B będzie także wierzchołkiem kąta który chcemy podzielić Niech prosta równoległa do AC i przechodząca przez B dzieli płaszczyznę na dwie półpłaszczyzny Na jednej z dwusiecznych obieramy sobie punkt D należący do tej samej półpłaszczyzny co punkty A oraz C Teraz wektor BD powinien leżeć na prawo od wektora AB i na lewo od wektora BC a sprawdzamy to badając znak wyrażenia (x_B − x_A)(y_C − y_A) − (y_B − y_A)(x_C − x_A) tyle że za A, B,C wstawiamy odpowiednie literki tak jak to w artykule na ważniaku napisali

chichi: @Mariusz przeczytaj linki, które Ci w tym osobnym wątku, tam jest na ten temat napisane

chichi: Mianowicie tu: https://www.math-only-math.com/bisector-of-the-angle-which-contains-the-origin.html

Mariusz: Tak ale ja w swoim programie korzystam z podejścia opartego na konstrukcji dwusiecznej jak pokazywałem u Szkolniaka a oni korzystają z porównywania odległości od ramion kąta

chichi: Rozumiem, póki co nie mam czasu rozmyślać nad Twoją metodą, teraz zajmuje się równaniami różniczkowymi. Dziś robiliśmy dogłębną analizę jednego przykładu, która zajęła 1.5h i żeśmy nie skończyli, no ale jak to na zajęciach wszystko trwa dłużej. Jeśli chcesz to się pobaw: Rozwiąż równanie 2y√by−y²dx − (b² + x²)dy = 0, gdzie b > 0

Mariusz: Ja ten program piszę tak dla zabawy zainspirowany pytaniem Szkolniaka Może później go wykorzystam do programu rysującego okrąg wpisany w trójkąt Z okręgiem opisanym na trójkącie byłoby mniej zabawy To jest zwykłe równanie o rozdzielonych zmiennych przy czym już masz pewne założenie na b No to liczymy 2y√by−y²dx − (b²+x²)dy = 0 | : (2yp{by−y²)(b²+x²)

dx		dy
	−		=0
b2+x2		2y√by−y2

przy czym tutaj wypadałoby poczynić założenia że to przez co dzielimy nie jest równe zero

dx		dy
	=
b2+x2		2y√by−y2

	dx		dy
∫		= ∫
	b2+x2		2y√by−y2

Pierwsza całka jest tablicowa do drugiej ładnie się sprawdzi trzecie podstawienie Eulera

1		dx
	∫		=
b2		x   1+( )2   b

1		1   dx b
	∫
b		x   1+( )2   b

	1		x
=		arctg(		)
	b		b

	dy
∫
	2y√by−y2

√by−y²=yt by−y²=y²t² y(b−y)=y²t² b−y = yt² b=y+yt² b=y(1+t²)

	b
y=
	1+t2

	bt
yt =
	1+t2

dy=b*(−1)(1+t²)⁻²(2t)dt

	−2bt
dy=		dt
	(1+t2)2

	1+t2	1+t2		−2bt
∫			(		dt)
	2b	bt		(1+t2)2

	1
−		∫dt
	b

	1
−		t +C1
	b

	dy		1		√by−y2
∫		= −		*		+C1
	2y√by−y2		b		y

1		x		1		√by−y2
	arctg(		)=−		*		+C1 | b
b		b		b		y

	x		√by−y2
arctg(		) = −		+ C2
	b		y

√by−y2		x
	= − arctg(		) + C2
y		b

I teraz czy zależy nam na postaci jawnej Jak tak to rozwiązujemy dalej

by−y2		x
	= (− arctg(		) + C2)2
y2		b

b		x
	− 1 = (− arctg(		) + C2)2
y		b

b		x
	= 1 + (− arctg(		) + C2)2
y		b

y		1
	=
b		x   1 + (− arctg( ) + C2)2   b

	b
y =
	x   1 + (− arctg( ) + C2)2   b

Problem w tym że podnoszenie do kwadratu nie jest przekształceniem równoważnym Na koniec sprawdzamy czy przez założenie (2yp{by−y²)(b²+x²) ≠ 0 nie straciliśmy rozwiązań

chichi: To nas uczą dużo bardziej formalnie rozwiązywania, pogubione rozwiązania, założenia przed całkowaniem, dziedzina etc. Dlatego mówiłem o wgłębnej analizie. A co odnośnie tej stałej, czy może być dowolna?

Mariusz: A to dlatego wam tyle zeszło Ba ja samemu czytałem o równaniach różniczkowych więc możliwe że nie rozwiązywałem tego zbyt dokładnie Co ze stałą mieliście coś o ograniczeniach na stałą podczas waszej analizy tego równania ? Gdy będziecie mieli zagadnienie Cauchyego to już stałej dowolnej nie będzie Czasem np jak bierzesz funkcję wykładniczą z obu stron równania to masz stałą dodatnią ale gdy jest to połączone z wartością bezwzględną to już w następnym kroku znowu mielibyśmy stałą dowolną Jakie tutaj zrobiliśmy przekształcenie abyśmy musieli ograniczyć stałą Jeżeli zostawiamy rozwiązanie w postaci uwikłanej to poprawność sprawdzamy wstawiając

	dy		δF   δx
za		−
	dx		δF   δy

chichi: Tak, tego było mnóstwo. Różne granice, z de L'Hospitalem, granice z ilorazu różnicowego, osobne badanie przypadków dla punktów wykluczonych przy założeniach przed całkowaniem, z których jedno okazało się być rozwiązaniem szczególnym, drugie zaś rozwiązaniem osobliwym etc. Masa pisania

Mariusz: Może dobrze że was tak uczą ale czy będziesz miał czas na taką analizę na egzaminie

chichi: Właśnie zapomniałem Ci powiedzieć, na kolokwium nie dokonujemy takie dogłębnej analizy, tylko rozwiązujemy do tego momentu, do którego Ty rozwiązałeś (jak mawia prof. "Krysicki by tu zakończył i my na kolokwium również, ale nie teraz i tutaj na zdjęciach") natomiast na ćwiczeniach zagłębiamy się w te równania i bardzo dokładnie je analizujemy oraz wszystkie jego rozwiązania. Natomiast co do egzaminu, to jest on z teorii dotyczącej równań różniczkowych i twierdzeń z nimi związanych − dowody etc.

Mariusz: Chichi a mógłbyś tak w punktach wypisać jak analizowaliście to równanie różniczkowe o rozdzielonych zmiennych ? Jeśli chodzi o mnie to tak tutaj trochę skróciłem to rozwiązanie i na kolokwium wypadałoby jeszcze pokazać co się dzieje w przypadku wykluczonym założeniem że nie dzielimy przez zero

chichi: @Mariusz jak znajdę czas i odkopię kiedyś Twój wątek z RR, to napiszę tam dogłębną instrukcję rozwiązywania RR tego typu

Mariusz: https://matematykaszkolna.pl/forum/385133.html Tu masz spis tematów z RR którymi się zajmowałem Niektóre punkty z tego spisu przydałoby się dokładniej rozpisać a niektóre punkty dopisać RR uczyłem się jednak samemu i możliwe że mam pewne braki Skończyłem studia informatyczne i to tylko te zaoczne

Mariusz: A możliwe że kiedyś przekopiowałem ten spis do innego wątku jak pisałem o RR z Damianem lub Szkolniakiem