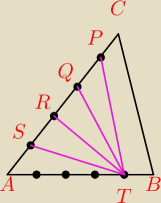
wykazywanie SP_ania: Punkty zaznaczone na bokach trójkąta ABC dzielą dwa jego boki na równe części. Wykaż, że pole każdego z trójkątów ATS, STR, RTQ,QTP stanowi 0,16 pola trójkąta ABC.

Kacper:

a7: 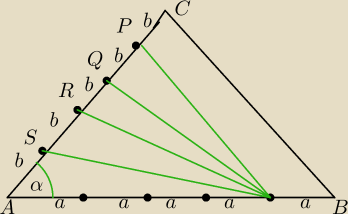https://matematykaszkolna.pl/forum/324509.html P_ABC=1/25a*5b*sinα=12,5absinα P_ATS=1/2*4a*bsinα=2absinα P₍STR}=P_ATR−P₍ATS}=1/2*4a*2bsinα−2absinα=2absinα P_RTQ=p_ATQ−P_ATR=1/2*4a*3bsinα−1/2*4a*2bsinα=2absinα P_QTP=P_ATP−P_ATQ=1/2*4a*4bsinα−1/2*4a*3bsinα=2absinα

2absinα
	=20/125=4/25=16/100=0,16 c.n.w.
12,5absinα

an: Czemu tak komplikować, proste zadanie

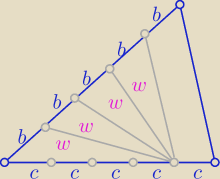
a@b: Każda środkowa dzieli trójkąt na dwa trójkąty o równych polach ( w )

	4
w=		P=0,16P
	25

SP_ania: a7 −> Nie wiem co to sinα, w klasie ósmej jeszcze tego nie mieliśmy

	4
a@b−> Nie rozumiem skąd wziąłeś to
	25

PW: Pomyśl najpierw o trójkącie ATP − co wiemy z twierdzenia odwrotnego do twierdzenia Talesa i co wiemy o polach trójkątów podobnych.

SP_ania: O ATP wiem, że jest równe 4*Pola AST i ATS=STR=RTQ=QTP, bo mają wspólną wysokość z T na podstawę, która w tych małych trójkątach jest tej samej długości. Nie miałam twierdzenia Talesa, a tym bardziej twierdzenia do niego odwrotnego.

a7: zaraz to zrobię na poziomie klasy 8

PW: a7, a nie sądzisz, że zmieniła nick, ale to ta sama osoba, co chce pomagać uczniowi podstawówki, ale nie zna podstawy programowej?

a7: no ale nie rozumiem, co w tym złego nie znać podstawy programowej i chcieć się dowiedzieć jak to zrobić chyba , że to zadanie na szóstkę...

PW: Osoba, o której myślę, to była kandydatka na nauczycielkę matematyki, bardzo roszczeniowa i uciążliwa.

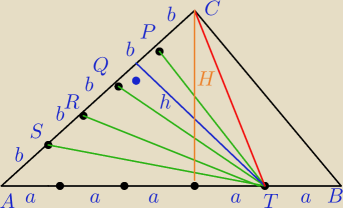
a7: P_ATC=1/2*5bh=1/2*4aH czyli aH=5/4*bh czyli P_TBC=1/2aH=5/8*bh P_ABC=P_ATC+P_TBC=1/2*5bh+5/8bh=25/8*bh P_AST=P_SRT=P_RQT=P_QTP=1/2*bh

1   *bh 2
	=0,16
25   bh 8

a7: to mnie nie było chyba jeszcze na forum jak ona tu była, chcesz powiedzieć, żeby nie robić zadań za nieuprzejme osoby,? ale ja też obserwuję, że osoby rozwiązujące zadania też czasami różnie z uprzejmością itp. jak uważasz, że to słuszne to możesz wykasować moje rozwiązanie − nie będę mieć żalu...

chichi: @PW też tak domniemywam

a7: chyba cos musiałam przegapić...

SP_ania: Dziękuję za pomoc a7 @PW − nie jestem żadną kandydatką na nauczycielkę matematyki. W poniedziałek mam sprawdzian z zadań z dowodzenia, wykazywania, itp. i niestety z niektórymi mam problem.

Mila: 1) P=P_ΔABC 2) Do rysunku 10:58 PT ||CB

	4b		4
ΔATP∼ΔABC w skali k=		=		⇒
	5b		5

	4		16
PΔATP=(		)2P=		P
	5		25

3) P_ΔATS=P _ΔSTR=P {ΔRTQ}=P_ΔQTP ( jednakowe podstawy i ta sama wysokość ) Zatem:

	16		4
PΔATS=(		P):4=		P=0,16P
	25		25