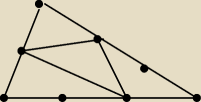
 W trójkącie ABC punkty D i E dzielą bok AB na trzy odcinki równej długości; punkty F i G
dzielą bok BC na trzy docinki równej długości, a punkt H jest środkiem boku AC.
Wykaż, że pole trójkąta EGH stanowi 5/18 pola trójkąta ABC.
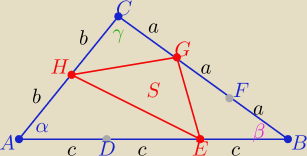
W trójkącie ABC punkty D i E dzielą bok AB na trzy odcinki równej długości; punkty F i G
dzielą bok BC na trzy docinki równej długości, a punkt H jest środkiem boku AC.
Wykaż, że pole trójkąta EGH stanowi 5/18 pola trójkąta ABC.
| 3c*3a | 2b*3c | 2b*3a | ||||
(**) P(ABC)=P= | *sinβ= | *sinα= | *sinγ | |||
| 2 | 2 | 2 |
| 2c*b | 1 | |||
P(AEH)= | *sinα to P(AEH)= | P ( z (**)porównując P | ||
| 2 | 3 |
| c*2a | 2 | |||
P(EBG)= | *sinβ to P(EBG)= | P | ||
| 2 | 9 |
| b*a | 1 | |||
P(CGH)= | *sinγ to P(CGH)= | P | ||
| 2 | 6 |
| 1 | 2 | 1 | 5 | |||||
zatem S= P−( | + | + | )P= .... = | P | ||||
| 3 | 9 | 6 | 18 |