Przekroje.
Marika : Ostrosłup prawidłowy czworokątny przecięto płaszczyzną prostopadłą do jednej z krawędzi
bocznych ostrosłupa
i jednocześnie zawierającą przekątną podstawy.
Otrzymany przekrój jest trójkątem rozwartokątnym, którego kąt rozwarty ma miarę 2α.
Wyznacz cosinus kąta β nachylenia płaszczyzny tego przekroju do płaszczyzny podstawy.
Z rysunkiem.
Z góry dziękuję.

Mila:
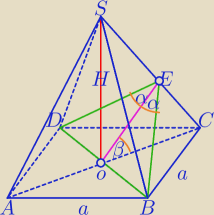
OE⊥SC, |BE|=|DE|, BE⊥SC,
DE⊥SC ,0<2α<180
o
1)
ΔDBE− Δprostokatny równoramienny
OE⊥DB
|DB|=a
√2
2)W ΔCOE:
cosβ=ctgα
================
Możesz ułatwić rachunki przyjmując długość podstawy : 2a

 OE⊥SC, |BE|=|DE|, BE⊥SC,
DE⊥SC ,0<2α<180o
1)
ΔDBE− Δprostokatny równoramienny
OE⊥DB
|DB|=a√2
OE⊥SC, |BE|=|DE|, BE⊥SC,
DE⊥SC ,0<2α<180o
1)
ΔDBE− Δprostokatny równoramienny
OE⊥DB
|DB|=a√2
