Równanie zespolone anonim123: Czy dobrze rozwiązałam równanie zespolone? https://zapodaj.net/343d3567d759d.jpg.html

ABC: zgroza co ty odp.... miałaś wzór de Moivre'a na pierwiastki zespolone ?

anonim123: A co jest źle?

wredulus_pospolitus: co to kuźwa jest (z³)² + 8² = −1[ − [ (z³)² − 8²] ] że niby jakim cudem proponuję tak: (z³)² + 8² = 0 (−1)*(−1)*(z³)² + 8² = 0 −(i *z³)² + 8² = 0 (8− iz³)(8 + iz³) = 0 (2³ + (−1)iz³)( 2³ − (−1)iz³) = 0 (2³ + (iz)³)(2³ − (iz)³) = 0 (2 + iz)(2² − 2iz + (iz)²)(2 − iz)(2² + 2iz + (iz)²) = 0 i rozwiązujesz dalej

wredulus_pospolitus: albo tak jak pisze @ABC ... jeżeli miałaś wzór de Moivre'a −−− to rozwiązujesz to w jednej linijce

anonim123: A tym wzorem to jak rozwiązać?

anonim123: ?

anonim123:

ABC: Możesz też zrobić tak :znajdź jedno rozwiązanie tego równania , a następnie pomnóż je przez pięć pierwiastków szóstego stopnia z jedynki nie będących jedynką − te pierwiastki leżą w wierzchołkach sześciokąta foremnego wpisanego w okrąg jednostkowy , jednym z wierzchołków jest punkt (1,0)

anonim123: A wzorem de Moivre'a jak?

ABC: przekształcając do postaci z⁶=−64

ICSP: https://matematykaszkolna.pl/forum/411742.html

anonim123: ABC a możesz to rozpisać?

ABC: nie chce mi się

anonim123: A ktoś inny?

Sushi: Wzór znasz?

anonim123: tak

Sushi: To go zapisz

anonim123: cos(6fi)+isin(6fi)=−64?

Sushi: Nazwy kątów masz w rubryce „inne” ω φ To nie jest wzór na „n−ty” pierwiastek

ABC: wejdź tu i przeczytaj wolno to co jest pod napisem :Twierdzenie https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html

anonim123: Ale wzór de Moivre'a jest chyba taki https://www.matemaks.pl/wzor-de-moivre-a-potegowanie-liczb-zespolonych.html a nie taki https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html

ABC: kwestia nazewnictwa , ten drugi niektóre książki też nazywają de Moivre'a w każdym razie zastosuj go

anonim123: nie widzę tego że można to rozwiązać w jednej linijce może ktoś pomóc?

anonim123: https://zapodaj.net/25c390a62fec6.jpg.html na razie zrobiłam tak

ABC: nie rokujesz dobrze na przyszłość , idź na konsultacje jeśli nie masz zdalnych jeszcze

anonim123: może ktoś pomóc?

ABC: każdy rozłożył ręce skoro ze strony matemaksa nie potrafisz podstawić do wzoru w którym jest pierwiastek arytmetyczny n−tego stopnia z modułu liczby podpierwiastkowej czyli u ciebie ⁶√64=2

anonim123: Dzięki

Mila: z⁶+64=0 1) sposób Z zastosowaniem wzorów de Moivre'a. z⁶=−64 |−64|=64 φ=π

	π+2kπ		π+2kπ
zk=6√64*(cos		+i sin		), gdzie k∊{0,1,2,3,4,5}
	6		6

	π		π
z0=2*(cos		+isin		)=√3+i
	6		6

	3π		3π		π		π
z1=2*(cos		+i sin		)=2*(cos		+i sin		)=2i
	6		6		2		2

	5π		5π		−√3		1
z2=2*(cos		+i sin		)=2*(		+i*		)=−√3+i
	6		6		2		2

	7π		7π		−√3		1
z3=2*(cos		+i sin		)=2*(		−i*		)=−√3−i
	6		6		2		2

	9π		9π		3π		3π
z4=2*(cos		+i sin		)=2*(cos		+i sin		)=−2i
	6		6		2		2

	11π		11π		√3		1
z5=2*((cos		+i sin		)=2*(		−i*		)=√3−i
	6		6		2		2

======================================

anonim123: Mila a jak to rozwiązać w jednej linijce?

daras: a Wy tu pracujecie teraz dla zapodaj.pl

Mila: II sposób i⁶=−1, bo i²+i²*i²=(−1)*(−1)*(−1)=−1 z⁶+64=0⇔ z⁶−(2i)⁶=0 z wzoru skróconego mnożenia: a²−b²=(a−b)*(a+b) (z³−(2i)³)*((z³+(2i)³)=0 teraz z wzorów: (a³±b³)=.. (z−2i)*(z²+2iz−4)*(z+2i)*(z²−2iz−4)=0⇔ z−2i=0⇔z=2i lub z+2i=0⇔z=−2i lub Dla trójmianów: Δ=12=4*3

	−2i−2√3		−2i+2√3
z=		=−√3−i lub z=		=√3−i
	2		2

lub

	2i−3√3		2i+√3
z=		=−√3+i lub z=		=√3+i
	2		2

z∊{√3+i,2i,−√3+i,−√3−i,−2i,√3−i} ===========================

chichi: @daras dla studentów, którzy Bóg wie jak w ogóle zdali maturę i dostali się na studia

ABC: Pięknie Mila

Mila: 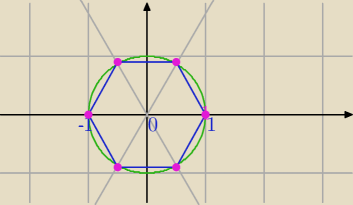anonim Pierwiastki 6−stopnia z jedynki− wierzchołki sześciokąta foremnego.

	1		√3		1		√3		1		√3		1		√3
{1,		+		i,−		+		i,−1,−		−		i,		−		i}
	2		2		2		2		2		2		2		2

Następnie pomnóż przez 2i , bo liczba 2i spełnia podane równanie . więc otrzymasz: 2i,1+√3, licz dalej Czy to jest krócej dla Ciebie?

Mila: 16:53 wg sugestii ABC 16:42

Mila: 2i, dobrze , 1+√3 źle napisałam, anonim popraw i licz dalej.

anonim123: wolę poprzednie sposoby tego średnio rozumiem

Mila: Pomnóż każdy element ze zbioru pierwiastków z jedynki i zobaczysz co wyjdzie. Współrzędne wierzchołków sześciokąta foremnego takiego jak na rysunku też przecież umiesz odczytać.