Postać trygonometryczna liczby zespolonej anonim123:

	3pi
Skąd mam wiedzieć że to jest kąt		?
	2

anonim123: https://zapodaj.net/5256b52b4dc04.jpg.html

wredulus_pospolitus:

	π		3π
cosα = 0 −−−> α =		∨ α =
	2		2

	3π
sinα = −1 −−−> α =
	2

teraz już wiesz

anonim123: to trzeba zapamiętać czy da się wyprowadzić?

wredulus_pospolitus: heeeee Potrafisz narysować wykres f(x) = cosx oraz g(x) = sinx Wybacz − ale jesteś na studiach To o co się pytasz to jest poziom gimnazjum / początek szkoły średniej. Nikt na uczelni nie będzie się zastanawiał czy potrafisz narysować wykres f(x) = cosx czy też nie. Każdy zakłada, że masz opanowany materiał szkół średnich.

anonim123: https://zapodaj.net/717f865e65802.jpg.html https://zapodaj.net/3fa3279f4e197.jpg.html Czy to zadanie dotąd jest dobrze i co dalej?

anonim123: Ok. Już wiem o co chodzi z tym kątem ale nie wiem 20:24

anonim123:

	pi
co zrobić z pi +		?
	6

wredulus_pospolitus: powtórz sobie (albo zajrzyj do): 'wzory redukcyjne funkcji trygonometrycznych'

debil: https://matematykaszkolna.pl/strona/430.html niektórzy mają wstret do po szukania wiedzy w podręczniku

chichi: @wredulus₋pospolitus a ja pragnę zauważyć, że autorka jest studentką matematyki...

anonim123: https://zapodaj.net/a798f4eb78ba1.jpg.html a co tutaj mam źle skorzystałam ze wzorów redukcyjnych

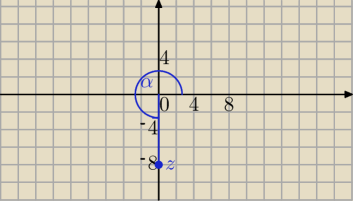
Mila: z=−8i Punkt na płaszczyźnie : (0,−8)

	3π
α=
	2

anonim123: Dalej nie wiem co mam źle bo dla k=1 i k=2 wychodzi mi to samo a tak nie powinno być

anonim123: Nie wiem z 21:26

chichi: Prosiłbym abyś z szacunku do ludzi, którzy chcą udzielić Ci tutaj pomocy nie wrzucała zdjęć takiego ochłapu, mi by było wstyd. Absurdalnym jest to, że na takie rzeczy trzeba zwracać uwagę

anonim123: https://zapodaj.net/9f56906bc77a8.jpg.html teraz lepiej?

anonim123: Przepraszam

anonim123: Czy dalej jest nieczytelnie? Co mam poprawić?

anonim123:

	pi
ten początek pi +		to jest dla k=1
	6

chichi: Nic z tego nie rozumiem, masz jakieś polecenie? Ty se coś podstwiasz, ja nawet nie wiem po co.

	π		√3
Dużo równości tu w ogóle nie zachodzi, jakim cudem cos(−		) = −		?
	6		2

anonim123: Robię zadanie z 19:56 liczę dla k=1 i k=2

chichi: Jak Ty wzorów nawet nie znasz...

anonim123: Możesz napisać jak policzyć dla k=1 i k=2 dla k=0 mam obliczone?

chichi:

	3π   +2nπ 2		3π   +2nπ 2
Powinno być tak: z = 2(cos(		) + isin(		)), n∊ℤ
	3		3

Teraz podstaw n∊{0, 1, 2}

anonim123: tak robiłam tylko najpierw liczyłam bez 2* coś wyliczyłam dla n=0 2i

chichi:

	π		π
Dla n=0: 2(cos(		) + isin(		)) = 2(0+i) = 2i
	2		2

	7π		7π		√3		i
Dla n=1: 2(cos(		) + isin(		)) = 2(−		−		) = −√3 −i
	6		6		2		2

	11π		11π		√3		i
Dla n=2: 2(cos(		) + isin(		)) = 2(		−		) = √3 − i
	6		6		2		2

Mam nadzieję, że wyczerpałem Twoje pytania...

anonim123: A dlaczego w 11:44 to jest źle bo nie wiem jak inaczej to zrobić dla k=0 mam dobrze obliczone

chichi:

	π		π		√3
Co jest źle o 11:44? cos(−		) = cos(		) =
	6		6		2

anonim123: już rozumiem