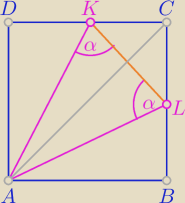
Optymalizacja - zadanie tekstowe Andzia: W kwadrat ABCD o danym boku a wpisano trójkąt równoramienny AKL w ten sposób, że wierzchołki L,K należą do odcinków DC i BC oraz AL=LK. Wyznacz największe i najmniejsze pole trójkąta AKL.

chichi: Szanowna Andzio, czy podjęłaś w ogóle jakąkolwiek próbę zrobienia tych zadań?

Andzia: Szanowny/a chichi, owszem podjęłam, zrobiłam rysunek, lecz to co mi wyszło nie za wiele mi dało... . Odnosząc się do rysunku, który zrobiłeś/aś, oznaczyłam sobie boki AK i AL jako b, boki kwadratu to a, bok DK jako x, CK w takim razie a−x bok BL jako y CL w takim razie a−y I z Twierdzenia Pitagorasa: AK²=AD²+DK² b²=a²+x² oraz AL²=AB²+BL² b²=a²+y² Przyrównując, b² mamy a²+x²=a²+y² zatem x²=y², zatem x=y a więc BL=x=DK CL=a−x=CK

Andzia: Nie wiem czy to co zrobiłam, w jakikolwiek sposób poprowadziło zadanie do przodu, ale wydaje mi się że tak, ponieważ z początku nie wiedzieliśmy (chyba), że BL będzie równe DK i CK będzie równe CL

chichi: ΔADK ≡ ΔABL ⇒ |CK| = |CL| (tak szybciej)

chichi: P_ABCD = P_ΔABL + P_ΔLCK + P_KDA + P_ΔAKL

Andzia: Faktycznie, ale jak w takim razie ugryźć to zadanie.. Jeszcze przyszło mi na myśl, że może w jakiś sposób wykorzystać fakt, że Pole trójkąta AKL to Pole kwadratu − te 3 pola trójkąta (z czego dwa są takie same), zatem by wyszło że P△AKL=a²−¹₂x², ale znowu ten sam problem, czy coś z tego wyniknie... Przyjmując, że CK=CL=x a BL=DK=a−x (wiem że oznaczenia na odwrót niż w 1 opisie, ale raczej większej róznicy to nie ma)

chichi: Musisz niestety zmienić rysunek, bo tak teraz czytam polecenie i tam jest AL=LK, a u mnie jest, że |AL|=|AK|...

chichi: Ale zadziałaj analogicznie, pitagoras oraz skorzystaj z rady o 19:43

Andzia: Rzeczywiście, więc teraz gdy już jest dobry rysunek, to czy te odcinki na które podzieliły boki punkty L i K będą równe, tak jak w tamtym przypadku?

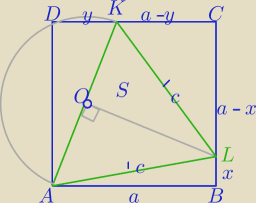
Mila: 1)a−x>0, a−y>0

	1
a2=		(a*y+(a−y)*(a−x)+ax)+S
	2

	a2−x*y
S=
	2

2) c²=a²+x² c²=(a−x)²+(a−y)² a²+x²=a²−2xa+x²+(a−y)² 2ax=(a−y)²

	(a−y)2
x=
	2a

3)

	1		y*(a−y)2
S=		*(a3−		)
	2		2a

	1
S(y)=		*(a3−y*(a−y)2)
	4a

	1
S'(y)=		*(−(a−y)2+(−y)*2(a−y)*(−1))
	4a

Posprawdzaj rachunki i dokończ 4)rozważ przypadek : y=0

chichi: No i tak rozwiązanie miałem na myśli, super @Mila

mat: https://matematykaszkolna.pl/forum/405050.html

Mila: Trzeba było wcześniej dać linka, to nie pisałabym

ite: po ożywieniu wygląda to tak 👉 https://www.geogebra.org/geometry/af9nqe9s

mat: Sorry,ale nie było mnie wcześniej na forum

Mila: Pięknie ite, tak to widziałam. Ciekawe, czy Andzia dokończy.

Andzia :

	1
Dzięki wielkie Mila, tylko czy S(y) nie powinno być		* (2a3−y(a−y)2)?
	4a

Bo ciągle mi tak wychodzi.. I ogolnie dlaczego Pole tego trójkąta uzależniamy od y a nie np od x? Ma to jakieś znaczenie?

Mila: Tak , zgubiłam 2 przy przepisywaniu, a potem kopiowałam Nie ma znaczenia , czy x, czy y , ale tutaj x łatwiej obliczyć.

Andzia : Okej dzięki jeszcze raz , a mogłabyś zerknąć jaki powinien być prawidłowy wynik pochodnej, bo wychodzą mi różne i juz sama się gubie

Mila: https://www.wolframalpha.com/input/?i=derivative%5B%282a%5E3%E2%88%92y%28a%E2%88%92y%29%5E2%29%2Cy%5D

Andzia : Dziękuję

Andzia: Mam jeszcze pytanie, bo dopiero teraz mam czas na dokończenie tego zadania i mam kłopot.

	−a2+4ay−3y2
Mianowicie po obliczeniu pochodnej która wynosi: S'(y)=		policzyłam Warunek
	4a

konieczny czyli: S'(y)=0, mianownik zawsze jest większy od 0 bo a>0, zatem −a²+4ay−3y²=0, po rozłożeniu mamy (y−a)(−3y+a)=0

	1
czyli y=a (to jest sprzeczne bo y<a) y=		a
	3

No i później Warunek dostateczny czyli S'(y)>0 czyli (y−a)(−3y+a)>0 no i to (y−a) jest sprzeczne, zatem wzielam pod uwage (−3y+a) no i z tego

	1
wychodzi że w x=		a będzie minimum lokalne, czyli mozemy wyznaczyć najmniejsze pole
	3

trójkąta, a co w takim razie z największym? Gdzie robię błąd?

Andzia:

	1
Przepraszam, tam minimum lokalne w y=		a
	3

Andzia: Jest ktoś w stanie mi wyjaśnić?

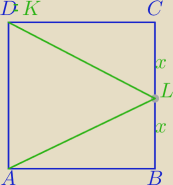
Mila: Największe pole w przypadku y=0. Wtedy mamy sytuację jak na rysunku L− środek BC

	a2
S=		( punkt (1) )
	2