Optymalizacja, trójkąt w kwadracie. Dratus: W kwadrat ABCD o danym boku a wpisano trójkąt równoramienny AKL w ten sposób, że wierzchołki L, K należą do odcinków DC i BC oraz AL = LK. Wyznacz największe i najmniejsze pole trójkąta AKL. Oczywiście na "chłopski rozum" największe pole będzie dla trójkąta prostokątnego równoramiennego (o ile się niemylę).

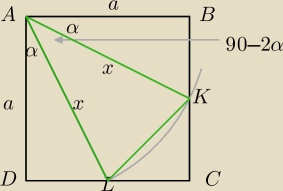
a7: P(x)=1/2x²sin(90−2α)=1/2x²cos2α=1/2x²(2cos²α−1)=1/2x²(2*a²/x²−1)=a²−1/2x² Pole będzie największe gdy x będzie jak najmniejszy czyli x=a wtedy P=1/2a² Pole będzie najmniejsze, gdy x będzie jak największy czyli x→a√2⁻ (?)

a7: ech, błędny rysunek

Dratus: Super, teraz mam trochę rozjaśnioną sytuację. Próbowałem robić na pola tych mniejszych trójkątów, ale to głupi pomysł. Dzięki raz jeszcze

Saizou :

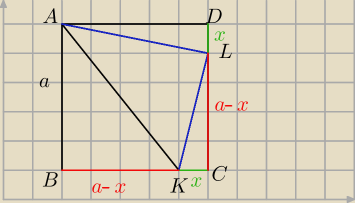
	1
P = a2 −		[a(a−x)+x(a−x)+ax]
	2

	1
P =		(x2−ax+a2)
	2

I dalej samemu

Eta: @ Saizou ? |AK|≠|AL| i |AL|≠|KL ΔAKL nie jest równoramienny

Saizou : Widziałem AL = LK :c, trzeba w końcu wybrac się do okulisty. no to post można usunąć

Saizou : Chociaż. W kwadrat ABCD o danym boku a wpisano trójkąt równoramienny AKL w ten sposób, że wierzchołki L, K należą do odcinków DC i BC oraz AL = LK. Wyznacz największe i najmniejsze pole trójkąta AKL.

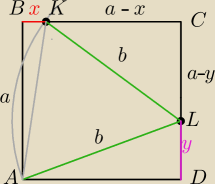
a7: P=a²−1/2ax−1/2(a−x−1/2(a−x)(a−y)−1/2ay=1/2a²−1/2xy niestety nie mam pomysłu

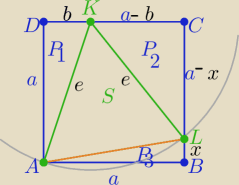
Eta: 1/ jeżeli B=L i D=K to mamy ΔABC o polu a²/2 2/ jeżeli B≠L i D≠K ( jak na rys.) i x∊<0,2) S=a²−(P₁+P₂+P₃) P₁=ab/2 , P₂=(a−b)(a−x)/2 i P₃= ax/2 P₂= a²−ax−ab+bx

	ab+a2−ax−ab+bx+ax		a2+bx
P1+P2+P3=		=
	2		2

	a2		x
S=		−		*b
	2		2

============= i teraz e²=a²+b² i e²= (a−b)²+(a−x)²

	(a−x)2
to b=
	2a

	a2		x
zatem S(x)=		−		(a−x)2
	2		4a

i działaj dalej.................

Eta: A Dartus ? .... pewnie na randce

Mila: Nic innego nie mam

Dratus: Dratus na randce , Dzięki Eta

Eta: