logika
anonim123: wyznacz wykresy następujących funkcji zdaniowych |xy|>0⇒|x|<|y| jak to zrobić

31 paź 16:55
Szkolniak:
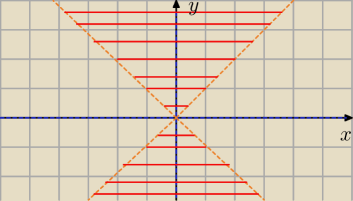
Na osiach przerywane linie (x≠0 ∧ y≠0). Ktoś potwierdzi czy tak to będzie wyglądało? To pokażę
jak do tego doszedłem

31 paź 17:42
ite:
Szukamy takich par liczb (rzeczywistych ?), dla których podana funkcja zdaniowa stanie się
zdaniem prawdziwym. Funkcja ma postać implikacji, a implikacja jest prawdziwa, gdy poprzednik
jest fałszywy lub następnik prawdziwy.
Szkolniak w takim razie trzeba znaleźć pary dające fałsz w poprzedniku oraz pary dające
prawdziwy następnik.
31 paź 19:49
Szkolniak: A to wybacz
ite, dosyć cienki jestem z logiki i chciałem tylko spróbować i sprawdzić czy
rozumiem zadanie

może za chwilę spróbuję drugi raz wraz z Twoją odpowiedzią
31 paź 20:11
kerajs:
Powyższy wykres może być. Wynik to zaznaczone fragmenty płaszczyzny (bez brzegów) wraz z osią
OX.
1 lis 08:37
ite:
kerajs dlaczego tylko oś OX?
z obiema osiami
1 lis 08:59
kerajs:
Ponieważ pisząc ''zaznaczone fragmenty płaszczyzny '' miałem na myśli także oś 0Y (bez (0,0) )
do nich należącą.
1 lis 22:22
anonim123: Może mi ktoś wyjaśnić jak Szkolniak do tego doszedł?
2 lis 17:57
kerajs:
Zaznaczasz obszary w których:
a) |xy|>0 ∧| x|<|y| (obie nierówności są prawdziwe)
b) |xy|≤0 (pierwsza nierówność jest fałszywa(a druga dowolna))
Szukanym obszarem jest suma obszarów a) i b)
*****************************************************************************
PATOLOGIĄ jest ukrywanie przed zbanowanym użytkownikiem
informacji: kto, ZA CO i na jak długo go ukarał.
PATOLOGIĄ jest usuwanie postów zgodnych z netykietą.
6 lis 10:19
Kacper:
kerajs? kto cię zbanował?
6 lis 13:11
anonim123: dzięki

6 lis 15:07
Mila:
Znowu coś się dzieje?
6 lis 16:24
Kacper: Ja bywam ostatnio w miarę systematycznie na forum i nic nie zauważyłem 🤔
7 lis 04:42
Mila:

Dziękuję.
7 lis 16:47
kerajs:
''Kacper:
kerajs? kto cię zbanował?''
W tym problem, że mimo moich pytań ani nie wiem kto blokował, ani za co. Ot, taka zmowa
milczenia.
Pewnie, że przy niektórych banach ( przykładowo jak tu:
https://matematykaszkolna.pl/forum/410499.html )
domyślam się kto i dlaczego, jednak nie we wszystkich mam taką pewność.
PS
Rzadko bywam i jakoś uciekł mi ten temat. Sorry.
27 lis 09:41

 Na osiach przerywane linie (x≠0 ∧ y≠0). Ktoś potwierdzi czy tak to będzie wyglądało? To pokażę
jak do tego doszedłem
Na osiach przerywane linie (x≠0 ∧ y≠0). Ktoś potwierdzi czy tak to będzie wyglądało? To pokażę
jak do tego doszedłem 
 może za chwilę spróbuję drugi raz wraz z Twoją odpowiedzią
może za chwilę spróbuję drugi raz wraz z Twoją odpowiedzią

 Dziękuję.
Dziękuję.