proszę o rozwiązanie anna: Wyznacz wszystkie wartości parametru m , dla których oba pierwiastki równania (3m + 1)x² − (4m + 1)x + 12m = 0 są większe od 2. ja to zadanie rozwiązałam a ostateczny wynik to

	−1		−1
m ∊ (		;		)
	3		4

ale nie wiem czy dobrze

wredulus_pospolitus: warunek: 1) a*f(2) < 0 −−−> (3m+1)*(4(3m+1) − (4m+1) + 12m) < 0 Z niego wyszedł mi inny przedział

wredulus_pospolitus: źle warunek zrobiłem winno być: a*f(2) >0 ∧ x_wierzchołka > 2

wredulus_pospolitus: a z tego NA PEWNO wyjdzie co innego niż Tobie

chichi: @wredulus₋pospolitus f(x) = x²−7x+12 f(2) = 2 ∧ a=1 ⇒a*f(2) = 2 > 0

chichi: A już zmieniłeś zdanie, ok

kerajs: ''wredulus_pospolitus: a*f(2) >0 ∧ x_wierzchołka > 2'' Wiesz, że te warunki spełniają także parabole nieprzecinające osi OX?

wredulus_pospolitus: zgoda ... jeszcze Δ > 0

wakacje:

	−5−√33		1
mi przedział wyszedł taki: m∊(		;−		), potwierdzicie?
	32		3

Mila: https://matematykaszkolna.pl/forum/409520.html

anna:

	−1		−1
1) xw > 2 ⇔ m ∊ (		;		)
	3		4

	−1
2) f(2) >2 ⇔ m >
	8

	−1
3) a>0 ⇔ m >
	3

	−5 −√33		−5 +√33
4) Δ > 0 ⇔ m ∊ (		;		)
	32		32

	−1		−1
1∩ 2∩3∩4⇒ m ∊ (		:		) chyba że się gdzieś pomyliłam
	3		4

wakacje: dzięki Mila

chichi: @anna a co gdy a < 0? Spójrz na rozwiązanie @Mila w linku, który podała

anna: dziękuję

	−3		−1
słusznie xw >2 ⇔m ∊ (		:		)
	8		3

i wakacje 14 paż 22:36 ma rację

kerajs: No to bardziej po szkolnemu: a≠0 ∧ Δ≥0 ∧ (x₁−2)(x₂−2)>0 ∧ (x₁−2)+(x₂−2)>0

chichi: @kerajs dlaczego dopuszczasz istnienie jednego rozwiązania?

kerajs: Ponieważ mierzi mnie współczesny bałagan i niezdecydowanie co do kwestii pierwiastków i rozwiązań, więc liczę jak dawniej, że dla zerowego wyróżnika trójmianu kwadratowego są dwa równe pierwiastki ( a podstawowe twierdzenie algebry ma treść: wielomian n−tego stopnia ma n pierwiastków (w ciele liczb zespolonych)).

kerajs: Ponieważ mierzi mnie współczesny bałagan i niezdecydowanie co do kwestii pierwiastków i rozwiązań, więc liczę jak dawniej, że dla zerowego wyróżnika trójmianu kwadratowego są dwa równe pierwiastki ( a podstawowe twierdzenie algebry ma treść: wielomian n−tego stopnia ma n pierwiastków (w ciele liczb zespolonych)).

Kacper: Mnie uczono innego twierdzenia zwanego zasadniczym twierdzeniem algebry, ale może od tego czasu coś się zmieniło w matematyce. 😁

chichi: Możesz tu zajrzeć: https://encyklopedia.pwn.pl/haslo/algebry-twierdzenie-podstawowe;3867784.html

Kacper: Osobiście wolę stwierdzenie, że wielomian o współczynnikach zespolonych ma pierwiastek zespolony. Również wolę powiedzieć, że równanie (x−1)¹⁰⁰=0 ma 1 rozwiązanie równe 1, a nie 100 równych rozwiązań A tak naprawdę wystarczy doprecyzować co autor ma na myśli i wszyscy są zadowoleni.

chichi: Ja podzielam Twoje zdanie, ale jak kto woli. Nigdy się spotkałem, aby ktoś mówił, że równanie kwadratowe dla Δ = 0 posiada dwa równe rozwiązania, ale jeszcze jestem młody

wredulus_pospolitus: Pragnę tylko napomnieć o tym, że niegdyś po prostu pierwiastek ≠ rozwiązanie rozwiązanie i owszem − było jedno (i pojedyncze miejsce zerowe miała funkcja w(x) ), ale pierwiastków mogło być więcej.

Kacper: Wiele stwierdzeń uległo dziwnej zmianie bądź.. zapomnieniu Taka ciekawostka, jaki ostrosłup nazywamy prostym?

wredulus_pospolitus: Kacper − jeżeli dobrze pamiętam, że prosty to taki w którym spodek wysokości jest w środku okręgu opisanego na podstawie

Kacper: Wredulus, ja kiedyś (na studiach) zajrzałem do podręcznika p. Zydlera i tam jest inna definicja. Dodatkowo, wg tej definicji o której mówisz (też tak mnie uczyli) to ostrosłup, którego podstawą jest trapez równoramienny może być "prosty" a jednak bardzo "krzywy". Spodek wysokości jest rzeczywiście w środku okręgu opisanego na podstawie, ale znajduje się poza podstawą, co powoduje, że patrząc na taki ostrosłup w ogóle nie mam wrażenia, że jest on prosty.

wredulus_pospolitus: przy takiej definicji (o ile tak było − bo piszę z pamięci) po prostu gwarantujemy sobie, że wszystkie krawędzie boczne tego ostrosłupa będą sobie równe. Co niesie za sobą równość kąta nachylenia krawędzi do podstawy.

Kacper: Ciekawi mnie idea, tego który wymyślał tę definicję. Czy bryła miała być prosta do liczenia, czy miała być prosta w potocznym mniemaniu (nie jak krzywa wieża w Pizie)

chichi: @wredulus₋pospolitus przecież to znane twierdzenia stereometrii, drugie mówi o tym, że jeśli wszystkie ściany boczne ostrosłupa są nachylone do podstawy pod takim samym kątem, to w podstawę można wpisać okrąg, a jego środek jest spodkiem wysokości P. S. Podzielam Twoją definicję, która pociąga za sobą to o czym mówisz, czyli ostrosłup prosty to taki, które wszystkie krawędzie boczne są równej długości, bądź wszystkie są nachylone pod tym samym kątem do płaszczyzny podstawy, bądź też spodkiem wysokości jest środek okregu opisanego na podstawie, to wszystko równoważne definicje

Kacper: 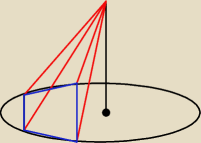chichi tak nas zapewne wszystkich uczono w szkole, ale ja bym takiego ostrosłupa nie nazwał prostym Dodatkowo ciekawy jest fakt, że w bardzo znanym podręczniku do geometrii definicja jest inna.

chichi: @Kacper mógłbyś proszę podać definicje z tego podręcznika? P. S. No jest trochę 'krzywy' haha, ale tu nie o to chodzi

Kacper: Ostrosłup nazywamy prostym, jeżeli w jego podstawę można wpisać koło, a spodek jego wysokości jest środkiem tego koła. Wszelki inny ostrosłup, który powyższych warunków nie spełnia, nazywamy pochyłym. zaczerpnięte stąd: http://www.wiw.pl/matematyka/geometria/geometria_13_04.asp#73

wredulus_pospolitus: no i czym się to różni od tego co wcześniej pisaliśmy

chichi: @Kacperi pojawia się pytanie kto to wszystko będzie rozstrzygał... Przypomniała się sytuacja, w której dostałem zjebe od profesora, wykładowcy za nazwanie wykresu funkcji f(x) = x³ parabolą sześcienną, której śmiało używał mój ćwiczeniowiec, co prawda spodobało mi się to pojęcie. Jak podaje Wikipedia i przytoczona sytuacja, jednego dnia coś może być poprawne i powszechnie używane, następnego zaś albo definicja diametralnie się zmieni bądź w ogóle zostanie wycofana.. Tutaj jest wzmianka o tym: https://pl.m.wikipedia.org/wiki/Parabola_sze%C5%9Bcienna

kerajs: Przypuszczam, że błędne pojmowanie własności ''prosty'' wynika z tego , że niemal wszystkie rozważane ostrosłupy są ''prawidłowe i proste'' , a uczniom wydaje się że spodek wysokości zawsze leży ''gdzieś w środku'' podstawy. @chichi ''Nigdy się spotkałem, aby ktoś mówił, że równanie kwadratowe dla Δ = 0 posiada dwa równe rozwiązania'' I ja także tak nie twierdzę. Dawniej nie utożsamiano pierwiastków z rozwiązaniami, więc zerowy wyróżnik wskazywał na JEDNO rozwiązanie, i DWA równe pierwiastki.