Dwusieczna kąta, geometria analityczna
wakacje: Pytanie o równanie dwusiecznej.
Zastanawiam się nad pewną rzeczą − mianowicie, niech dany będzie trójkąt w układzie
współrzędnych (znamy współrzędne jego wierzchołków)
Chcąc wyznaczyć równanie dwusiecznej jednego z kątów wewnętrznych, wyznaczamy równania dwóch
prostych, między którymi znajduje się dany kąt
Teraz niech P będzie punktem, który leży na tej dwusiecznej, jest równo oddalony od boków
Niech P=(x,y), no i tworzymy równanie, z którego powstają dwa rozwiązania
I pytanie do którego dążę: w jaki sposób rozróżnić albo wiedzieć (bez rysowania), która prosta
jest dwusieczną kąta wewnętrznego?
Bo druga prosta nie leży w trójkącie w ogóle
24 wrz 00:19
chichi:
Współczynniki kierunkowe prostych!

24 wrz 00:43
Mariusz:
Zastanawiam się czy taki sposób wyznaczenia równania dwusiecznej byłby poprawny
Mając dane wierzchołki trójkąta ABC
piszemy równania prostych w których zawierają się ramiona kąta
Na jednym z ramion kąta obieramy sobie punkt D
Piszemy równanie okręgu o środku w punkcie A i promieniu AD
Punkt E to przecięcie okręgu z prostą zawierającą drugie ramię kąta
(wybieramy punkt bliżej punktu B)
Piszemy równanie prostej przechodzącej przez punkty DE
Piszemy równanie prostej prostopadłej do prostej DE i przechodzącej przez punkt A
Można też wymyślić sposób wyznaczania równania dwusiecznej
bazując na sposobie jej konstrukcji
24 wrz 13:39
chichi:
Ale co masz problem w określeniu poprawności swojego rozumowania? Dlaczego?

24 wrz 14:47
chichi:
Sposób jest jak najbardziej poprawny, ale nieco dłuższy od 'standardowego'

24 wrz 14:53
Mariusz:
No właśnie ciekawy jestem jak wyglądałby dowód poprawności tego sposobu z 24 wrz 2021 13:39
Jeżeli chodzi o moje rozumowanie to wyszedłem ze sposobu konstrukcji dwusiecznej
ale w pewnym momencie go zmodyfikowałem
24 wrz 16:44
chichi:
To wszystko bazuje na stworzenie trójkąta równoramiennego na ramionach kąta, którego podziału
chcemy dokonać, a reszta wynika wprost z własności tegoż trójkąta

24 wrz 17:16
chichi:
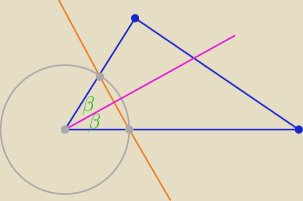
24 wrz 17:24
(--.--):
Można wykorzystać sposób ze współrzędnymi środka okręgu wpisanego w trójkąt.
24 wrz 18:22
Mariusz:
A jak znajdziesz te współrzędne bez równań dwusiecznych
24 wrz 18:27
Mariusz:
Ja przedstawiłem sposób znalezienia równania bazujący w znacznym stopniu
na sposobie konstrukcji dwusiecznej natomiast nie bardzo wiem jak chciałbyś wykorzystać
współrzędne środka okręgu wpisanego w trójkąt
24 wrz 19:36
:=:
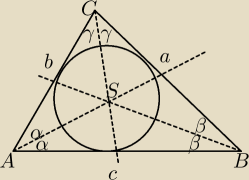
24 wrz 20:23
Mariusz:
No nadal nie bardzo wiadomo skąd się wziął twój wzorek na te współrzędne środka okręgu
Sposób który zaprezentowałem może i jest trochę dłuższy od tego "standardowego"
ale wynika z rozważań kroków konstrukcji i chichi z grubsza napisał dlaczego działa
24 wrz 22:28
chichi:
@
Mariusz to nie jest z grubsza 'napisane' tylko dowód bez opisu, to zostawiłem dla
czytelników, rozumowanie to przeprowadza się w głowie 'czytając" rysunek

24 wrz 23:01
wakacje: Co masz na myśli poprzez współczynniki kierunkowe prostej, chichi?
Myślałem że może chodzi Ci o to, że mając dwie proste można łatwo sprawdzić która z nich jest
malejąca a która rosnąca, no i z tego jakiś szybki szkic zrobić?
Ale jeśli będziemy mieli współrzędne w symbolach to wtedy chyba ciężko.
Ogólnie mam zadanie takie, że mam wykazać że jeśli współrzędne wierzchołków są liczbami
wymiernymi, to współrzędne środka okręgu wpisanego w trójkąt też są wymierne
:=: podał/a coś podobnego czego bym szukał, ale nie wiem czy to to
25 wrz 22:28
chichi: Bzdura totalna, mogą być np. obie ROSNĄCE, startujemy od wierzchołka i teraz zobacz jak
zachowują się współczynniki i zrób ograniczenie

25 wrz 22:53
wakacje: Przykładowo A=(a
1,b
1) oraz B=(a
2,b
2) oraz C=(a
3,b
3)
1) Prosta przechodząca przez punkty A oraz B: k: y=ax+b
b
1=a
1a+b ∧ b
2=a
2a+b
| | b1−b2 | | a1b2−a2b1 | |
⇒ a= |
| ∧ b= |
| |
| | a1−a2 | | a1−a2 | |
| | b1−b2 | | a1b2−a2b1 | |
k: y= |
| x+ |
| → (a1−a2)y−(b1−b2)x−(a1b2−a2b1)=0 |
| | a1−a2 | | a1−a2 | |
2) Prosta przechodząca przez punkty A oraz C: l: y=ax+b
l: (a
1−a
3)y−(b
1−b
3)x−(a
1b
3−a
3b
1)=0
3) Szukamy równania dwusiecznej kąta ∡BAC:
Tworzymy równanie:
| |(a1−a2)y−(b1−b2)x−(a1b2−a2b1)| | |
| = |
| √((a1−a2))2+(b1−b2)2 | |
| | |(a1−a3)y−(b1−b3)x−(a1b3−a3b1)| | |
= |
| |
| | √((a1−a3))2+(b1−b3)2 | |
No i z tego wychodzą dwa równania, dwóch prostych, w postaci y=ax+b − pytanie teraz jak w takim
momencie rozpoznać tę właściwą wersję?
Nie wiem czy mnie rozumiecie.. może trochę zagmatwałem
25 wrz 22:58
mat:
A może w treści jest : "środka okręgu opisanego
26 wrz 00:14
wakacje: Na to wychodzi, przepraszam za pomyłkę.. teraz już trzeba pamiętać, że 'circumscribed circle'
to okrąg opisany, a 'inscribed circle' to okrąg wpisany
To w takim razie zadanie już chyba teraz łatwo udowodnić tylko pewnie dużo żmudnej roboty i
przekształceń, zaraz może rozwiąże i ktoś w przyszłości akurat może skorzysta
26 wrz 01:30
mat:
No to po sprawie
− współczynniki kierunkowe prostych zawierajacych boki są wymierne
− współrzędne środków boków są wymierne środki
− współczynniki kierunkowe symetralnych boków też wymierne
to równania symetralnych mają i wyrazy wolne wymierne
− układ równań o współczynnikach wymiernych
ma rozwiązania wymierne
co oznacza,że środek S −− okręgu opisanego ma współrzędne wymierne
koniec dowodu
26 wrz 01:43
wakacje: w sumie tak słownie też można, więc rachunkowo jednak sobie odpuszczę, za późna godzina

jeszcze raz wybaczcie za pomyłkę i dzięki za wszelką pomoc
26 wrz 01:58
Mariusz:
Napisałem sobie w Pascalu programik do znajdowania równania dwusiecznej
sposobem konstrukcyjnym ale chyba nie oprogramowałem wszystkich przypadków
https://pastebin.com/DMkgYyey
29 paź 23:06
Mariusz:
student , jaką dwusieczną wybrać ?
Współczynnik kierunkowy to tangens kąta nachylenia prostej do osi OX
(można z tego wyprowadzić wzór na tangens kąta między wektorami)
Iloczyn skalarny wektorów to ab = |a||b|cos(α)
(Przyjmując że a oraz b są wektorami kolumnowymi
iloczyn skalarny można zinterpretować za pomocą iloczynu macierzy aTb)
30 paź 06:16
Szkolniak: Jako że to mój post, tylko że pod innym nickiem, to odpowiem
Mariusz, u mnie jeśli chodzi o jakiekolwiek programowanie to kompletnie nie czuję chęci
aby się tego uczyć i nie ciągnie mnie do tego, także ja akurat nie skorzystam z tego programu
do Pascala
31 paź 14:29
Mariusz:
Szkolniak a jak tam ci poszło z przećwiczeniem równań różniczkowych
Spis tematów który przedstawiłem w wątku
https://matematykaszkolna.pl/forum/385133.html
(patrz ostatni wpis)
to wg mnie takie minimum jeśli chodzi o równania różniczkowe zwyczajne
Pewnie jakiś nauczyciel albo ten kto niedawno miał równania różniczkowe na wykładzie
dołożyłby pewnie kilka tematów
Tutaj ja poległem na wymyślaniu ci przykładów do przećwiczenia
a w zbiorach zadań nie znalazłem odpowiednich
Co do równań wielomianowych to proponuję przejrzeć następujące pdf
http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf
https://pdfhost.io/v/s9Ezc.ZYP_redniowiecze.pdf
W tym drugim pdf jest krótko wspomniany sposób rozwiązywania
równania trzeciego stopnia używany przez Francoisa Viete
choć ja wolę ten przedstawiony u Sierpińskiego
7 lis 07:45
Szkolniak: Mariusz, jeśli chodzi o równania różniczkowe to trzymałem się tego co mi tam wysyłałeś i
robiłem po kolei Twoje przykłady, ale na koniec nie miałem już za bardzo czasu i też przez to
przestałem je rozwiązywać, bo nie było zwyczajnie kiedy
Teraz zaczęły mi się studia i siedzę w analizie matematycznej 1, którą myślę że
rozumiem, także następne za co się wezmę to pewnie analiza 2 aby nie było problemów z
zaliczeniem
Potem zobaczymy, jak mam się zabierać za takie równania różniczkowe to z pewnością trzeba
więcej czasu, a czterech działów na raz też nie chcę poruszać
A za linki dzięki wielkie, w wolnym czasie przejrzę i zobaczę o co tam chodzi
15 lis 21:19
Mariusz:
Szkolniak czytałeś o otoczce wypukłej
Tam było porównywanie kątów
a porównywało się je licząc pole równoległoboku rozpiętego na dwóch wektorach
Może to by się przydało do wyboru dwusiecznej
Problemem w napisaniu programu do wyznaczania równania dwusiecznej
sposobem konstrukcyjnym byłoby możliwe dzielenie przez zero
Z jednej strony postać kierunkowa jest wygodniejsza podczas losowania punktu D
(losujemy tylko jedną współrzędną a drugą obliczamy z równania prostej)
oraz podczas porównania równania okręgu z równaniem prostej zawierającej
drugie ramię kąta
Z drugiej zaś strony równanie ogólne prostej nie wymaga dzielenia
11 mar 18:23








 jeszcze raz wybaczcie za pomyłkę i dzięki za wszelką pomoc
jeszcze raz wybaczcie za pomyłkę i dzięki za wszelką pomoc