trójkąt
mirek:
W dowolnym trójkącie ABC o boku AC=b poprowadzono środkową AD,
na której zaznaczon punkt M,który jest jej środkiem .
Prosta BM przecina bok AC w punkcie E
Wyznacz długość odcinka AE
18 wrz 21:42
Mila:
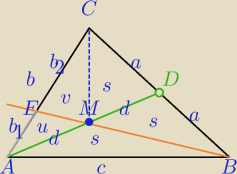
Małymi literami s, u i v zaznaczono pola Δ.
1) u+v=s
P
Δ=4s
stąd : v=2u
2)
b
2=2b
1
b
1+2b
1=b
========
18 wrz 22:51
Mila:
chichi, rozwiąż z wykorzystaniem Laader Theorem

Ja obliczyłam tylko stosunek pola ΔABM do pola ΔABC.
18 wrz 23:05
Mila:
Ladder
18 wrz 23:32
chichi:
@
Mila zabrzmiało jak rozkaz, ale wiem, że nie to miałaś na myśli. Jutro wrzucę jakieś
ciekawe rozwiązania, rozważę również Twoją propozycję

18 wrz 23:40
Mila:


Jaki rozkaz? To prośba przecież.
18 wrz 23:44
chichi:
@
Mila sam kontekst zadania prowokuje do syntetycznych rozważań hah... Wiem

Piszę z telefonu, wrócę pewnie nad ranem, więc spodziewaj się rozwiązań nieco później jutro

18 wrz 23:54
Mila:
II sposób
P
ΔABC=4s
| 1 | | 1 | | 1 | | 1 | |
| + |
| = |
| + |
| stąd : |
| 4s | | s | | u+s | | s+s | |
s=3u
s=u+v
3u=u+v, v=2u
b
2=2b
1 i b
1+b
2=b
=======
19 wrz 00:03
Mila:
To miłej imprezy życzę

Dobranoc.
19 wrz 00:05
aabb:
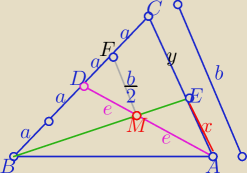 ===========
===========
19 wrz 00:39
Szkolniak: Mila, czy byłabyś mi w stanie proszę wytłumaczyć skąd w Twoim rozwiązaniu (18 wrz 22:51)
wiadomo, że pole trójkąta ABM jest również równe s?
19 wrz 22:39
Mila:
1) AD jest środkową w ΔABC⇒ Trójkąty ΔCDM i ΔBDM mają równe pola ozn. s
2)BM jest środkową w ΔABD⇒Trójkąty : ΔAMB i ΔDMB mają równe pola j.w. − s
3) Analogicznie ΔAMC i ΔDMC mają równe pola − s
Po ustaleniu, że PΔABC=4s można działać dalej.
Można jeszcze inaczej rozwiązać, ale już nie będę pisać, sam wymyśl.
19 wrz 22:53
19 wrz 22:57
Szkolniak: Super, już teraz rozumiem. Do zrozumienia brakowało mi zauważenia tego punktu (2).
Rozwiązać zadanie już próbowałem i nie umiałem, także staram się przynajmniej teraz wasze
rozwiązania zrozumieć, może wyciągnę coś na przyszłość

19 wrz 23:00
chichi:
A nie, teraz przeczytałem polecenie.. Myślałem, że M to barycentrum, sorry mb

19 wrz 23:00
Szkolniak: Dojść do równości u+v=s można też w inny sposób:
Środkowa AD dzieli ΔABC na dwa trójkąty: ΔADC oraz ΔABD
PΔADC=PΔABD ⇒ u+v+s=s+s ⇒ u+v=s
19 wrz 23:25
aabb:

19 wrz 23:30
 Małymi literami s, u i v zaznaczono pola Δ.
1) u+v=s
PΔ=4s
Małymi literami s, u i v zaznaczono pola Δ.
1) u+v=s
PΔ=4s
 Ja obliczyłam tylko stosunek pola ΔABM do pola ΔABC.
Ja obliczyłam tylko stosunek pola ΔABM do pola ΔABC.


 Jaki rozkaz? To prośba przecież.
Jaki rozkaz? To prośba przecież.
 Piszę z telefonu, wrócę pewnie nad ranem, więc spodziewaj się rozwiązań nieco później jutro
Piszę z telefonu, wrócę pewnie nad ranem, więc spodziewaj się rozwiązań nieco później jutro 
 Dobranoc.
Dobranoc.



