pole trójkąta gość: W trójkącie ABC dane są boki: AC=3, BC=4 i wiadomo, że środkowe: AE i BD są prostopadłe Oblicz pole trójkąta ABC.

chichi: (1) Środkowa to odcinek łączący wierzchołek Δ ze środkiem przeciwległego boku (2) Punkt przecięcia środkowych dzielnie je w stosunku 2:1 licząc od wierzchołka (3) Twierdzenie Pitagorasa Tyle Ci powinno wystarczyć

Szkolniak: Mi pole wyszło równe √11, może ktoś potwierdzi? Tylko że rozwiązanie dosyć beznadziejne, także nie zamieszczam

Mariusz: Co dokładnie proponujesz ? Co mogłoby zadziałać Podzielić ten trójkąt na mniejsze trójkąty, osobno policzyć pola i je dodać Policzyć wysokość spuszczoną na jeden z boków o danej długości Policzyć sinus kąta między bokami o danej długości

chichi: @Szkolniak okej

Mariusz: Na rysunku który sporządziłem w Geogebrze dla sprawdzenia wyniku Szkolniaka wyszło że wynik Szkolniaka może być poprawny

chichi: @Mariusz potwierdzam bez GeoGebry, że ten wynik jest poprawny na pewno

Szkolniak: Ja wybrałem twój pierwszy pomysł @Mariusz, podzieliłem ten trójkąt na pięć mniejszych i osobno liczyłem każde pole

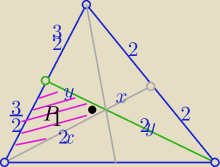
Eta: P(ABC)= 6P₁=6xy P²(ABC)=36x²y² z tw. Pitagorasa 4x²+y²=9*4 i 4y²+x²=4 to ............. y²=1/3 i x²=11/12

	1		11
P2=36*		*		=11
	3		12

P=√11 =====

Eta: Poprawiam zapis 4x²+y²=9/4

chichi: No i takie rozwiązanie miałem na myśli, brawo @Eta

Eta: Jeszcze mała poprawka: x²=1/3 i y²=11/12

Mariusz: No dobrze ale skąd wiemy że pola tych trójkątów są sobie równe

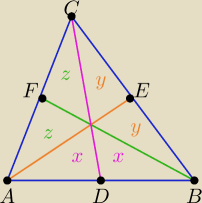
chichi: P_ΔACD = P_ΔBCD ⇒ 2z+x = 2y+x ⇒ z=y P_ΔABE = P_ΔACE ⇒ 2z+y = 2x+y ⇒ x=z Zatem: x=y=z, P_ΔABC = 2x+2y+2x = 6x = 6y = 6z To ja dorzucę jeszcze tylko to

chichi: Ooo, dobrze, że napisałem, bo w trakcie pisania zapytał się o to @Mariusz

Eta: Znane twierdzenie: trzy środkowe dzielą trójkat na sześć trójkątów o równych polach

Mariusz: chichi to że trójkąty których pola powierzchni oznaczyłeś tymi samymi literkami mają podstawy tej samej długości to widać ale mogłeś jeszcze zaznaczyć że mają wspólną wysokość a tak poza tym to ładny rysunek i opis tego rysunku

chichi: @Mariusz no, ale widzisz, dałeś radę wpaść na to samo i o to chodzi P.S. Uznałem, że za dużo będzie wszystkiego na rysunku, obszar roboczy na mało pozwala

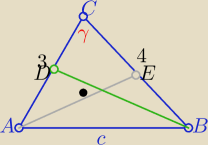
Eta: 2 sposób

	|AC|2+|BC|2
c2=		=...=5
	5

	9+16−5		5		√11
cosγ=		=		to sinγ=
	2*3*4		6		6

	1		√11
P(ABC)=		*3*4*		= √11
	2		6

Mariusz :

	|AC|2+|BC|2
c2=
	5

a to skąd się wzięło ?

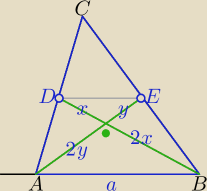
Mila: Spróbuj sam wykazać. AE⊥BD − środkowe prostopadłe.

	a
DE=
	2

5 |AB|²=|AC|²+|BC|² ==================== skorzystaj z tw. Pitagorasa

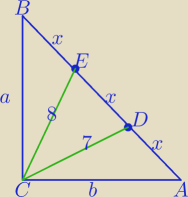
Mila: Dla maturzystów: Oblicz długość przeciwprostokątnej trójkąta prostokątnego , dane na rysunku:

chichi: Ale z poziomu podstawowego

Mila: Szkolniak jest "rozszerzony".

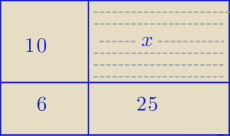
Mila: Podstawa : Oblicz pole prostokąta oznaczonego literą x

chichi: @Mila brzydki wynik swoją drogą do tego pierwszego zadania

Szkolniak: @Mila, ja już nie taki maturzysta, w tym roku pisałem i w końcu z głowy a wynik to

	3√565
		?
	5

Mariusz: "5 |AB|²=|AC|²+|BC|² ==================== skorzystaj z tw. Pitagorasa " Jakoś tego nie widzę a z twierdzenia Pitagorasa prędzej obliczyłbym długość AB niż wykazał tę równość

chichi: @Szkolniak zgadza się

Mila: Dobrze Szkolniak, przepraszam za pomyłkę w etapie edukacji Mariusz , pomyśl jeszcze. Jutro napiszę ja albo może chichi ?.

Szkolniak: Swoją drogą jak zrobiliście te zadanie? Ja poprzez podwójne skorzystanie z twierdzenia cosinusów dla kąta przy wierzchołku A (trójkąty CAD i CAE), a Wy?

chichi: Jednym działaniem

Mariusz: Szkolniak ja jak bawiłem się twierdzeniem cosinusów to wypisałem cztery równania na pięć niewiadomych (przy czym w jednym przypadku twierdzenie cosinusów zredukowało się do twierdzenia Pitagorasa)

Szkolniak: chichi jakie to działanie? Mariusz to ja na początku próbowałem chyba tak samo jak Ty, ale stwierdziłem że to bez sensu i sobie odpuściłem Też próbowałem z pól albo z faktu że środkowa dzieli trójkąt na dwa trójkąty o równych polach

chichi: @Mariusz na rysunku są 3 niewiadome (co i tak jest za dużo) to skąd ty masz aż 5?

chichi:

	5		3√565
82+72 =		|AB|2 ⇒ |AB| =
	9		5

Mariusz: Szkolniak do tego trzeba było jeszcze zastosować definicję cosinusa znaną jeszcze z podstawówki (przynajmniej za moich czasów w podstawówce jeszcze taka była) Ad 1 wrz 2021 23:33 W taki sposób stosowałem to twierdzenie cosinusów że wprowadziłem oznaczenia na kąty na które został podzielony ten kąt prosty i stąd pięć niewiadomych

Mariusz: Ad 1 wrz 2021 23:39

	5
Trzeba by było jeszcze równość 82+72=		|AB|2
	9

wykazać inaczej mogliby tego maturzystom nie uznać

chichi: No i tu właśnie jest ten pies pogrzebany, bo korzystamy z gotowego wzoru, a przecież korzystam z wielu gotowych wzorów wcale ich na maturze nie udowadniając P. S. Wrzucić Ci @Mariusz dowód tego wzoru? Można również to rozumowanie, które przedstawię w dowodzie zastosować po prostu jako rozwiązanie do tego zadania, ale ja pokażę wyprowadzenie wzoru dla ogółu takiej sytuacji w trójkącie prostokątnym

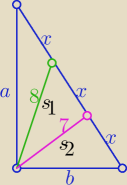
Eta: Dodać stronami kwadraty długości środkowych s₁ i s₂ 4s₁²=2a²+2*7²−4x² 4s₂²=2b²+2+2*8²−4x² i a²+b²=9x² otrzymamy to co podał chichi 5x²=7²+8²

	9*113
9x2=
	5

	3√565
3x=|AB|=
	5

Eta: Poprawiam zapis 4s₂²=2b²+2*8²−4x²

Mariusz: A mnie się wydaje że jednak podczas wprowadzania jakiegoś twierdzenia bądź wzoru raczej podają także i dowód poprawności A jak korzystasz z twierdzenia bądź wzoru którego nie wymagają na maturze to jednak wypadałoby podać dowód poprawności Ad P.S możesz wrzucić

chichi: 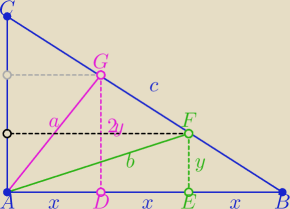Rysunek − tw. Talesa oraz liniowa środkowa w trójkącie!

	c
|BC| = c ⇒ |FB| =
	3

(1) ΔADG: x²+4y²=a² (2) ΔAEF: 4x²+y²=b² (3) Dodając stronami mamy, że: a²+b² = 5(x²+y²)

	c2
(4) ΔFEB: x2+y2 =
	9

	c2		5
(5) a2+b2 = 5(x2+y2) ∧ x2+y2 =		⇒ a2+b2=		c2 □
	9		9

Mariusz: Eta skąd te równania bo z twierdzenia cosinusów to dostalibyśmy raczej to s₁²=a²+x²−2axcos(β) s₂²=b²+x²−2axcos(α) Z definicji cosinusa

	a
s12=a2+x2−2ax(		)
	3x

	b
s22=b2+x2−2bx(		)
	3x

	1
s12=		a2+x2
	3

	1
s22=		b2+x2
	3

	1
s12+s22=		(a2+b2)+2x2
	3

Z twierdzenia Pitagorasa a²+b²=9x² zatem

	1
s12+s22=		* 9x2 +2x2
	3

s₁²+s₂²=5x² 5x²=7²+8² 5x²=113

	9*113
9x2=
	5

	3√565
3x=
	5

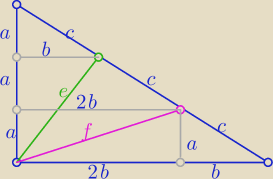
Eta: e²−4a²+b² f²=a²+4b² + −−−−−−−−− e²+f²=5(a²+b²) i a²+b²=c²

	e2+f2
c2=
	5

	e2+f2
3c=3√
	5

Eta: https://pl.wikipedia.org/wiki/%C5%9Arodkowa_tr%C3%B3jk%C4%85ta

chichi: Przecież to jest to samo co napisałem o godz. 01:18

Mariusz: Wg mnie na rozwiązanie Szkolniaka najłatwiej wpaść Ja gdybym trochę dłużej pobawił się twierdzeniem cosinusów to też bym na nie wpadł za to rozwiązanie chichiego jest dość pomysłowe i może się podobać

Mariusz: Zadanie z prostokątami cd=10 ab=41+x bc=16 cd=10 c(b−d)=6 a(b−d)=31 c(b+d)=26 c(b−d)=6

	32
2b=
	c

	20
2d=
	c

6a
	=31
c

	16
b=
	c

	10
d=
	c

	31c
a=
	6

	16
b=
	c

	10
d=
	c

31c	16
		=41+x
6	c

31*8
	=41+x
3

248
	=41+x
3

	248−123
x=
	3

	125
x=
	3

Jednak czy aby na pewno dobrze ?

chichi: No wszystko okej, ale rozwiązanie...

	25*10		125
x =		=
	6		3

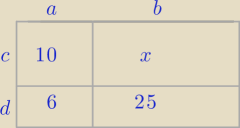
Mila: Zadanie z Ligi zadaniowej dla SP. ( około 10 lat temu) I sposób

10		a
	=
x		b

6		a
	=
25		b

10		6
	=
x		25

6x=10*25

	125
x=
	3

II sposób a*c=10 a*d=6 b*c=x b*d=25 =========== abcd=6x abcd=250 6x=250

	125
x=
	3

========

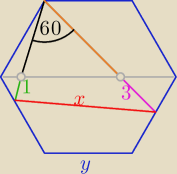
chichi: To i ja coś wrzucę coś od siebie, poziom rozszerzony. Polecenie: Dany jest sześciokąt foremny. Znajdź x oraz y.

Marcelli: Przygotowuje sie wraz z moja korepetytorka do zblizajacego sie sprawdzianu z planimetri z matematyki rozszerzonej i rozwiazujemy zadania z tego forum ale rozwiazujac to zadanie na rozne sposoby nie da dojsc sie do rozwiazania. Prawdopodobnie to zadanie jest zle skonstruowane a niektore nasze proby moge opublikowac jako dowod tego ze nie ma rozwiazania. Wyglada na to ze autor zadania zapomnial o jakims elemencie badz osoba chichi ktora to wrzucila. A zadania publikowane na tym forum sa naprawde ciekawe i rozwiazania uzytkownikow rowniez. Te ze planimetri bo narazie takie rozwiazywalismy.

an: Marcelli musisz wysłać swoją korepetytorkę na korepetycje, sam rachunek x=7 można obliczyć na paluszkach. No chyba, że przedstawisz te dowody, to zdejmę czapkę.

chichi: Pani Korepetytor również przydałyby się porządne korepetycje... A co z 'y'? Nie ma co wrzucać zadań, bo i tak nikt nie rozwiązuje

an:

	20
Jak chcesz koniecznie to Ci podam y=		, choć gdy ja miałem sprawdziany z planimetrii
	√21

nawet nie chcę pisać kiedy to było, myślałem, że poda ktoś bardziej zainteresowany.

chichi: Wynik poprawny, ta tutaj ktoś bardziej zainteresowany, proszę Cię..

Mila: Mnie interesuje każde nietypowe zadanie. To było Twoje zadanie i Ety− tak zrozumiałam. Może rozwiążę dla siebie, jak zadanie z równoległobokiem, mieliście pisać rozwiązanie, ale nie widzę.

chichi: Śmiało możesz wrzucić, tamto zadanie jest banalne i dlaczego 'miałem' wrzucić rozwiązanie?

ite: Dobrze jak po wpisaniu zadania jest zostawiany czas na zastanowienie się nad nim. Ale skoro nikt uczący się do matury nie rozwiązał go, lepiej zawsze zakończyć wątek rozwiązaniem. W przyszłości jeszcze pewnie ktoś do niego zajrzy, a najwięcej się korzysta na takich zamkniętych poprawnym rozwiązaniem wątkach.

an: Do @ ite mogę pomóc rozwiązać, ale gotowców nie daję leni nie wspieram, a w Polsce zbyt dużo ludzi ma maturę, a nawet wyższe wykształcenie przy wiedzy na poziomie szkoły przysposobienia rolniczego.

ite: Napisałam, że przyda się rozwiązanie, bo akurat tym wątku nikt nie czekał na gotowca z cudzą pracą (od lenia do jelenia). To pracowity chichi dał maturzystom szansę poćwiczenia : ), ale bez odzewu.