Trygonometria Szkolniak:

	β		a+c
Wykazać, że jeżeli w trójkącie cot(		)=		, to trójkąt jest prostokątny.
	2		b

Co w takiej sytuacji, gdy występuje połówka kąta? Mógłbym prosić o jakąś wskazówkę jak lewą stronę przekształcić?

mat:

	ctg2x−1
ctg2x =		, https://matematykaszkolna.pl/strona/1543.html
	2ctgx

biorąc x= β/2 masz

	(a+c)2/b2−1
ctgβ =
	2(a+c)/b)

nie wiem czy to pomoze

chichi:

	x		1+cos(x)		sin(x)
cot(		) =		=
	2		sin(x)		1−cos(x)

mat:

	a+c
a+c>b z nierówności trójkąta zatem		>1
	b

czyli ctg(β/2) > 1 a to oznacza, że β/2 < 45^o wiec β < 90^o ale to dalej mało..

mat: Czym jest w ogóle β Jakiś kątem w tym trójkącie czy wiadomo którym?

Szkolniak: Właśnie z ciekawości pobawię się teraz tym wzorem pierwszym który dałeś mat, bo właśnie sam próbuje go jakoś wyprowadzić Na temat kąta beta nie ma podanej żadnej informacji

chichi: Ale zaproponuję inny dowód a = 2Rsin(α) b = 2Rsin(β) c = 2Rsin(γ)

	β		sin(α)+sin(γ)
cot(		) =		⇔
	2		sin(β)

β   cos( )   2		α+γ   α−γ   sin( )cos( )   2   2
	= =
β   sin( )   2		β   β   sin( )cos( )   2   2

	α+γ		π		β
α+β+γ = π ⇒		=		−
	2		2		2

	β		π   β   α−γ   sin( − )cos( )   2   2   2
cos(		) =		⇔
	2		β   cos( )   2

	β		β   α−γ   cos( )cos( )   2   2
cos(		) =		⇔
	2		β   cos( )   2

	β		α−γ		β		α−γ
cos(		) = cos(		) ⇔		=		⇔ β = α−γ
	2		2		2		2

	π
α+β+γ = π ∧ β = α−γ ⇒ α =		□
	2

Szkolniak: Dowód ładny, pytanie tylko skąd się wzięła ta pierwsza linijka, pierwsza równość?

mat: twierdzenie sinusów

chichi:

	β		2Rsin(α)+2Rsin(γ)		2R[sin(α)+sin(γ)]
cot(		) =		=		⇔
	2		2Rsin(β)		2Rsin(β)

	β		sin(α)+sin(γ)
cot(		) =
	2		sin(β)

chichi:

	a
2R=		⇒ a = 2Rsin(α)
	sin(α)

	b
2R=		⇒ b = 2Rsin(β)
	sin(β)

	c
2R=		⇒ c = 2Rsin(γ)
	sin(γ)

Szkolniak: Już wszystko jasne, dzięki Swoją drogą można też do tego podejść w taki sposób, że powstaje równanie

	1+cos(x)		a+b
		=
	sin(x)		c

Teraz wyrazić można cos(x) za pomocą długości boków (a, b oraz c) poprzez twierdzenie cosinusów i zostaje sinus, macie jakiś pomysł jak go zamienić na długości boków?

chichi: Skoro masz cosinusa, to przecież z 1 tryg. dobierzesz się do sinusa, czyż nie?

Szkolniak: Próbowałem w ten sposób ale nie do końca to wychodzi, powstaje na końcu jeden czynnik którego nie da się nijak rozłożyć, także odpada Pomyślę jeszcze nad jakimś innym rozwiązaniem

Mila:

	β		p*(p−b)
1) ctg2(		)=		z wzorów na funkcje kątów Δ w zależności od połowy
	2		(p−a)*(p−c)

	a+b+c
obwodu: p=
	2

p*(p−b)		a+c
	=
(p−a)*(p−c)		b

wyjdzie jak trzeba.

Mila: Na jakie studia dostałeś się?

Mila: Ma być:

p*(p−b)		a+c
	=(		)2
(p−a)*(p−c)		b

Szkolniak: W takim razie rozwiążę dla potomnych, może ktoś kiedyś skorzysta: p(p−b)b²=(p−a)(p−c)(a+c)² p(p−b)b²−(p−a)(p−c)(a+c)²=0 4p(p−b)b²−4(p−a)(p−c)(a+c)²=0 2p(2p−2b)b²−(2p−2a)(2p−2c)(a+c)²=0, p=a+b+c (a+b+c)(a+b+c−2b)b²−(a+b+c−2a)(a+b+c−2c)(a+c)²=0 (a+b+c)(a−b+c)b²−(−a+b+c)(a+b−c)(a+c)²=0 (a+b+c)(ab²−b³+b²c)−(b+c−a)(a+b−c)(a²+2ac+c²)=0 a²b²−ab³+ab²c+ab³−b⁴+b³c+ab²c−b³c+b²c²=(b+c−a)(a+b−c)(a²+2ac+c²) a²b²+2ab²c−b⁴+b²c²=(b+c−a)(a+b−c)(a²+2ac+c²) a²b²+2ab²c−b⁴+b²c²=(ab+b²−bc+ac+bc−c²−a²−ab+ac)(a²+2ac+c²) a²b²+2ab²c−b⁴+b²c²=(b²+2ac−c²−a²)(a²+2ac+c²) a²b²+2ab²c−b⁴+b²c²=a²b²+2ab²c+b²c²+2a³c+(2ac)²+ +2ac³−a²c²−2ac³−c⁴−a⁴−2a³c−a²c² −b⁴=2a²c²−c⁴−a⁴ a⁴−2a²c²+c⁴−b⁴=0 (a²−c²)²−b⁴=0 (a²−c²−b²)(a²−c²+b²)=0 a²=b²+c² v a²+b²=c² Masz rację @Mila, wyszło wszystko ok

	β
Mam jednak do Ciebie pytanie − w jaki sposób zaczęłaś wyrażanie cot2(		) w ten sposób, w
	2

jaki to zrobiłaś? A jeśli o studia to zdecydowałem się na mechanikę i budowę maszyn na Politechnice Wrocławskiej, gdzie na szczęście problemu z dostaniem się nie było Jednak ciekaw jestem jaki będzie tam poziom na matematyce

Mila: Skorzystałam z tablic z wzorów na funkcje kątów Δ w zależności od połowy obwodu:

	A		(p−b)(p−c)
tg		=(		)1/2
	2		p(p−a)

Kiedyś to wyprowadziłam, a teraz można z tablic korzystać więc skorzystałam.

Mila: Rachunki mam krótsze

mat:

	1
P =		absinα −−−> z tego można wyliczyć ctgα w zależności od P, a, b
	2

P = .... wzór Herona i stąd łącznie można wyliczyć ctgα w zależności od a, b, c (ewentualnie z użyciem symbolu p − połowy obwodu)

Mila: Poziom wysoki na PWr. Mają dobre materiały dydaktyczne.

chichi: Znani Panowie z serii podręczników Marian Gewert i Zbigniew Skoczylas są prowadzącymi na PWr

Mila: Właśnie miałam polecić podręczniki M. Gewert i Z. Skoczylas. Szkolniakowi, poszukaj w internecie. Są w pdf−ie.

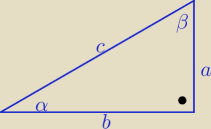
Eta: Można też tak: w odwrotną stronę Załóżmy,że trójkąt jest prostokątny to przekształcając równoważnie

	β		cosβ+1		a   +1 c		a+c
ctg		=		=		=
	2		sinβ		b   c		b

chichi: Nie jest to poprawny dowód

Szkolniak: Spróbuję skorzystać z wpisu mata: Niech 2p=a+b+c

	β		sin(β)
(1) cot(		)=
	2		1−cos(β)

(2) Z twierdzenia cosinusów:

	a2+c2−b2
cos(β)=
	2ac

	1
(3) P=√p(p−a)(p−b)(p−c) oraz P=		ac*sin(β)
	2

Porównujemy wzory:

	1
		ac*sin(β)=√p(p−a)(p−b)(p−c)
	2

acsin(β)=2√p(p−a)(p−b)(p−c)

	2√p(p−a)(p−b)(p−c)
sin(β)=
	ac

	sin(β)		2√p(p−a)(p−b)(p−c)
		=
	1−cos(β)		ac(1−cos(β))

	β		2√p(p−a)(p−b)(p−c)
cot(		)=
	2		a2+c2−b2   ac(1− )   2ac

	β		2√p(p−a)(p−b)(p−c)
cot(		)=
	2		2ac   a2+c2−b2   ac( − )   2ac   2ac

	β		2√p(p−a)(p−b)(p−c)
cot(		)=
	2		2ac−a2−c2+b2   ac( )   2ac

	β		2√p(p−a)(p−b)(p−c)
cot(		)=
	2		2ac−a2−c2+b2   2

	β		4√p(p−a)(p−b)(p−c)
cot(		)=
	2		2ac−a2−c2+b2

	β		4√p(p−a)(p−b)(p−c)
cot(		)=
	2		b2−(a−c)2

	β		4√p(p−a)(p−b)(p−c)
cot(		)=
	2		(b+a−c)(b−a+c)

	β		16p(p−a)(p−b)(p−c)
cot2(		)=
	2		(a+b−c)2(b−a+c)2

	β		16p(p−a)(p−b)(p−c)
cot2(		)=
	2		(a+b+c−2c)2(a+b+c−2a)2

	β		16p(p−a)(p−b)(p−c)
cot2(		)=
	2		(2p−2c)2(2p−2a)2

	β		16p(p−a)(p−b)(p−c)
cot2(		)=
	2		16(p−c)2(p−a)2

	β		p(p−a)(p−b)(p−c)
cot2(		)=
	2		(p−c)2(p−a)2

	β		p(p−b)
cot2(		)=
	2		(p−c)(p−a)

Trochę mi to nie dawało spokoju, Mila, i postanowiłem że sam spróbuję to wyprowadzić Jedynie z czego skorzystałem bez własnej wiedzy to punkt (1), z tej równości nigdy nie korzystałem

Szkolniak: A jeśli chodzi o książki Gewerta i Skoczylasa to mam na telefonie jakieś dwie ich książki, jedna to wzory i definicje a drugie to przykładowe kolokwia Na telefonie mam w sumie ich sporo, bo kiedyś dużo pobierałem i tak czekają − mam na przykład: Banaś i Wędrychowicz − zbiór zadań Krysicki i Włodarski − dwa tomy z analizy Sierpiński − teoria liczb Walter Rudin − podstawy analizy matematycznej Ryszard Rudnicki − wykłady z analizy matematycznej Fichtenholz − 3 tomy rachunku różniczkowego i całkowego I coś tam jeszcze by się pewnie znalazło.. niby książki są ale trochę ciężko mi się korzysta z nich na telefonie, także na razie tak wiszą

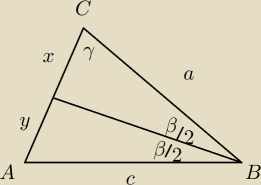
Minato: Z tw. o dwusiecznej

x		y		ay
	=		→ c =
a		c		x

β

a+c

ay   a+   x

ax+ay

a(x+y)

a

ctg(

) =

=

=

=

=

2

b

b

bx

bx

x

WNIOSEK: γ jest kątem prostym

Mila: 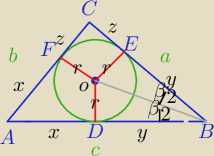Szkolniak, bardzo się napracowałeś.

	β		p*(p−b)
1) Wykazać, że ctg2		=
	2		(p−a)*(p−c)

	a+b+c
p=		; P=p*r ; P=√p*(p−a)*(p−b)*(p−c)
	2

2) W ΔDOB:

	β		y		β
ctg		=		⇔ y=r*ctg
	2		r		2

=========== y=c−x=c−(b−z)=c−b+z=c−b+(a−y)=c+a−b−y

	a		c		b		a+b+c
2y=a+c−b ⇔ y=		+		−		=		−b=p−b
	2		2		2		2

	β		P		β
3) (p−b)=r*ctg		⇔ p−b=		*ctg
	2		p		2

	β
p*(p−b)=√p*(p−a)*(p−b)*(p−c)*ctg		/2
	2

p2*(p−b)2		β
	=ctg2
p*(p−a)*(p−b)*(p−c)		2

	β		p*(p−b)
ctg2		=
	2		(p−a)*(p−c)

=====================

Szkolniak: Minato, jeśli chodzi o Twój wniosek to na pierwszy rzut oka chyba nigdy bym tego nie wywnioskował, w wolnym czasie spróbuję zobaczyć skąd to się bierze Miła, Twoje rozwiązanie rozumiem i dziękuję za takie wyjaśnienie, ale jeśli chodzi o taki dowód to raczej bym na niego nie wpadł. A wynika to z tego że geometria dosyć cienko u mnie i dokonując takich przekształceń jak Ty, czułbym ze prowadzi mnie to donikąd A napracowanie to nie aż takie straszne, na forum kopiuj wklej i leci bardzo szybko

jc: A może wykorzystać wzór na ctg podwojonego kąta?

	1
ctg β =		(ctg β/2 − tg β/2)
	2

a		1		a+c		b
	=		(		−		)
b		2		b		a+c

2a(a+c)=(a+c)²−b² a²+b²=c²