trójkat
loki: Udowodnij, że istnieje tylko jeden trójkąt, którego boki są kolejnymi liczbami naturalnymi, a
jeden z kątów jest dwukrotnością drugiego kąta.
26 sie 07:43
I'm back:
No i jak. Jakieś pomysły, domysły?
26 sie 08:28
26 sie 10:06
mat: Może twierdzenie sinusów?
26 sie 10:06
kerajs:
A co z przypadkami:
2. Kąt α leży naprzeciwko boku n, a 2α naprzeciwko boku n+1
3. Kąt α leży naprzeciwko boku n−1, a 2α naprzeciwko boku n
26 sie 10:48
Eta:
Sprawdź sobie sam

26 sie 11:03
moderator:
Nie zamierzam. Wskazuję jedynie na niekompletne rozwiązanie.
26 sie 11:17
kerajs:
Ups, nie ten nick
Poprawka:
Nie zamierzam. Wskazuję jedynie na niekompletne rozwiązanie.
26 sie 11:18
Eta:

26 sie 11:19
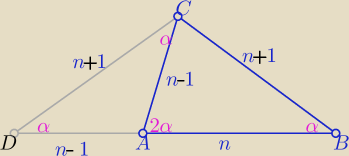 Podobnie jak tu:
https://matematykaszkolna.pl/forum/411044.html
n>1
Z podobieństwa trójkątów................
Podobnie jak tu:
https://matematykaszkolna.pl/forum/411044.html
n>1
Z podobieństwa trójkątów................


