wynik do zadania
gabi03: Dany jest trójkąt ABC, w którym |AB|=18 oraz |BC|=30. Wiedząc, że ∠BAC=2∠BCA wyznacz jego pole.
Czy ktoś mógłby podać mi sam wynik albo rozwiązanie bo mi wychodzi dziwnie

25 sie 21:02
chichi:
Jak może być sam wynik, to stawiam na S = 80
√11 
25 sie 21:10
gabi03: Ojjjj to ja mam inny wynik ciekawe kto ma zle?
25 sie 21:16
I'm back:
To pokaż swoje obliczenia. Sprawdzimy
25 sie 21:18
gabi03: A ty jaką masz odpowiedz I'm back?
25 sie 21:24
wredulus_pospolitus: taką samą jak chichi −−− pokaż obliczenia ... jakby co mam 'gotowego gotowca'

25 sie 21:25
gabi03: Ja mam ze P=162
25 sie 21:28
wredulus_pospolitus:
czego nie rozumiesz w tekście: "pokaż obliczenia"

25 sie 21:30
chichi:
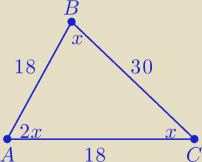
Mi amigo... widzę, że wyszło Ci , że |AC|=18, ale niestety należy to odrzucić, gdyż:
4x=180
o ⇒ 2x=90
o → ΔABC jest równoramienny, prostokątny, zatem |BC|=18
√2≠30 SPRZECZNE!
25 sie 21:32
chichi:
W trakcie Twojego rozwiązania powinna pojawić się druga możliwość, mianowicie |AC|=32 i tę
należy przyjąć jako właściwą, bo jeżeli rozumowanie jest poprawnie przeprowadzone, to powinny
pojawić się dwie możliwości na |AC|

25 sie 21:35
wredulus_pospolitus:
chichi ... jak liczyłeś pole? Ja wyznaczyłem sin(∡ABC)
25 sie 21:37
gabi03: Tak mam też że a=32 bo wyszło mi z równania kwadratowego. A skąd wiedzieć którą odpowiedź
wybrać?
25 sie 21:44
wredulus_pospolitus:
ponownie napiszę −−− POKAŻ SWOJE OBLICZENIA

25 sie 21:45
chichi:
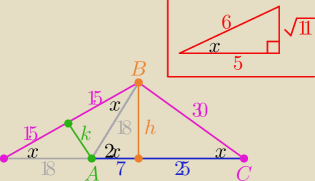
@
wredulus−pospolitus coś dorysować i... korzystam z takich
trójkącików i mam, że:
| | 32*5√11 | |
S = |
| = 80 √11  (k=3 √11 oraz h=5 √11) |
| | 2 | |
25 sie 21:50
wredulus_pospolitus:
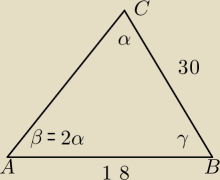
No to ja poszedłem całkowicie inną drogą, czyli bawiłem się trygonometrią:
wychodzimy z tw. sinusów:
| 5 | | 5 | | √11 | |
| = 2cosα −−−> cosα = |
| −−−> sinα = |
| |
| 3 | | 6 | | 6 | |
| | 5√11 | | 7 | |
−−> sin(2α) = |
| −−> cos(2α) = |
| |
| | 18 | | 18 | |
| | √11*7 + 5*5√11 | |
sin γ = sin(180 − (α+β)) = sin(α+β) = sinα*cosβ + cosα*sinβ = |
| = |
| | 6*18 | |
| | 1 | | 18*30*8√11 | |
PΔ = |
| ab*sinγ = |
| = 80√11 |
| | 2 | | 54 | |
25 sie 21:51
chichi:
" A skąd wiedzieć którą odpowiedź wybrać?"
Czy czytałeś mój wpis z
21:32 ?

25 sie 21:53
chichi:
Równie sprytnie @
wredulus−pospolitus, dobre rozwiązanie. Ja wolę bez tryg...

25 sie 21:56
wredulus_pospolitus:
@chichi −−− gabi to raczej kobita

25 sie 22:01
gabi03: ja mam tak
1)sinx=h/30
2)sin2x=h/18
2sinxcosx=h/18
sinx=h/36cosx
3)h/30=h/36cosx
cosx=5/6
4)182=a2+302−2∙a∙30∙5/6
324=a2+900−50a
a2−50a+576=0
Δ=2500−2304=196
a1=50+14/2=32 lub a2=50−14/2=18
i wzięłam to a2 nie wiem które wziąć?
25 sie 22:02
Mila:
Gabi jaki masz wynik?
chichi mam trochę inny wynik.
√11 zgadza się.
25 sie 22:08
chichi:
@
wredulus−pospolitus myślałem, że gabi−on, ale 'wzięłam' potwierdza, że kobita. Dzięki

@
gabi03 czytasz w ogóle nasze posty? Wyjaśniłem Ci wyżej, jak wyeliminować odpowiedź
|AC|=18... można to zrobić też tak:
| | 5 | | 5 | | 7 | |
cos(x)= |
| ⇒ cos(2x)=2*( |
| )2−1= |
| |
| | 6 | | 6 | | 18 | |
Tw. Carnota musi zachodzić również dla ∠BAC:
| | 7 | |
302=|AC|2+182−2|AC|*18* |
| ⇒ |AC|=32 ∨ |AC|=−18 |
| | 18 | |
Które rozwiązanie jest wspólne? (ale polecam eliminację z
21:32 oczywiście)

25 sie 22:10
chichi:
@
Mila nie chce wyjść inaczej... @
wredulus−pospolitus potwierdził mój wynik

25 sie 22:12
gabi03: Mila ja mam że P=162 i nie wiem czemu mam źle a ty ile masz?
25 sie 22:14
wredulus_pospolitus:
gabi −−− jeżeli wychodzą dwie możliwości to bierzesz pod uwagę obie tak długo jak długo któraś
ich nie odpadnie ze względu na jakieś założenia.
25 sie 22:14
chichi:
@
Mila pokaż rozwiązanie

25 sie 22:16
wredulus_pospolitus:
@gabi −−− masz źle bo przy otrzymaniu dwóch wartości ostatniego boku, wybrałaś sobie (na ślepo)
jedną z nich nie sprawdzając czy to w ogóle ma sens.
25 sie 22:16
gabi03: Aha już rozumiem chichi nie widziałam tego. Sprawdzę teraz dla a=32 i powiem co wyszło
25 sie 22:17
gabi03: zrobiłam tak
p=18+32+30/2=40
P=pierw(40∙22∙8∙10)
P=pierw(6400∙11)
P=pierw(6400)∙pierw(11)
P=80∙pierw(11)
25 sie 22:23
wredulus_pospolitus:
gabi ... błagam cię −−− NAWIASY
 (
(18+32+30
)/2

(wcześniej też napisałaś h/36cosx zamiast h/(36cosx) )
Wierz mi −−− to jest ogromna różnica

25 sie 22:28
Eta:
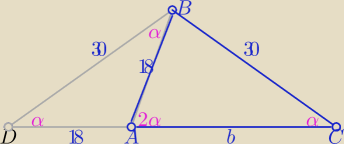
Z podobieństwa trójkątów równoramiennych DBC i DAB
| | 30 | | 18 | |
|
| = |
| ⇒ 18b=302−182 ⇒ b=32 |
| | 18+b | | 30 | |
Ze wzoru Herona
P(ABC)=
√40*10*8*22=
√4*10*4*2*2*11
P= 80
√11
=======
Pozdrawiam

25 sie 22:28
chichi:
√4*10*4*2*2*11 = 8
√110 
25 sie 22:32
chichi:
@
Eta zgubiłaś dychę

25 sie 22:33
Eta:
Tak , zgadza się ( to banał)

25 sie 22:34
gabi03: Muszę jeszcze policzyć pole trójkąta w trapezie równoramiennym jak się tutaj rysuje?
25 sie 22:38
Eta:
Poprawiam "chochlika"
P=
√40*10*8*22=
√4*10*10*4*2*2*11=80
√11
teraz pasuje ?

25 sie 22:39
chichi:
Super @
Eta 
, @
gabi03 nad oknem pisania w prawym górnym rogu
rysuję 
25 sie 22:41
Mila:
Ja miałam błąd rachunkowy.

25 sie 22:43
gabi03:
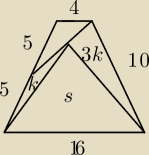
Polecenie to tylko Wyznacz S.
25 sie 22:48
gabi03: Ja na to zadanie nie mam nawet pomysłu a wy? Może za mało informacji
25 sie 22:57
chichi:
Wystarczająco.. S=52, rozwiązanie zostawiam Paniom

P.S. Zakładaj nowe posty, jeśli wstawiasz nowe zadanie

25 sie 23:08
gabi03: A czemu taki wynik?
25 sie 23:38
kerajs:
Może stąd, że pole niezaznaczonego trójkąta wynosi 8 j2, a jego najdłuższy bok liczący √65 j
dzielony jest przez wspólny wierzchołek trzech trójkątów w stosunku (od lewej) 5:3, co sprawia
iż k=5 j2.
26 sie 10:36
chichi:
Brawo Panie @
kerajs, chociaż rozwiązanie mam nieco inne

26 sie 12:24
Mariusz:
Z wcześniej wymienionego wzoru Herona wynika że wynik S=52 jest fałszywy
| | 16+k+3k | |
Połowa obwodu to |
| = 8 + 2k |
| | 2 | |
√(2k+8)(2k−8)(8+k)(8−k)=52
(4k
2−64)(64−k
2)=2704
4(k
2−16)(64−k
2)−2704=0
(k
2−16)(64−k
2)−676=0
(k
2−16)(k
2−64)+676=0
k
4−80k
2+1024+676=0
k
4−80k
2+1700=0
(k
2−40)
2+100=0
i co k zespolone ?
26 sie 13:53
chichi:
@
Mariusz 'k' i '3k' to pola tych trójkątów, nie zaczynaj znowu..

26 sie 14:00
Mariusz:
Z rysunku to nie wynika ale gdyby przyjąć że 'k' i '3k' to pola tych trójkątów to wynik może
być
Po tym jak przyjrzałem się wpisowi kerajsa to on też założył że 'k' i '3k' to pola tych
trójkątów
Tak przy założeniu że 'k' oraz '3k' pola tych trójkątów to nawet tyle wyjdzie
o ile kerajs nie pomylił się w obliczeniach
Co do wpisu kerajsa to
Skąd wziął długość boku w tym 'niezaznaczonym trójkącie'
Skąd wziął ten stosunek
Jak znajomość tego stosunku oraz długości tego boku pozwala obliczyć k
26 sie 16:08
wredulus_pospolitus:
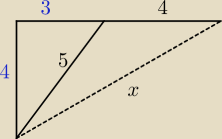
stąd wziął x
2 = 4
2 + 7
2
26 sie 16:14
wredulus_pospolitus:
a wiemy, że dopisywany jest trójkąt prostokątny 3,4,5 z tego, że wcześniej policzyliśmy
wysokość trapezu: h = 8
26 sie 16:15
Mariusz:
Wredulus ok długość boku już mamy
Tak wysokość trapezu też policzyłem i wyszła mi taka jak tobie
a co z tym stosunkiem no i jak mając stosunek i długość boku obliczyć k
26 sie 16:25
Mariusz:
Gdy będziemy mieli objaśniony sposób uzyskania wyników podanych przez kerajsa
to będziemy mogli od pola trapezu
(średnia arytmetyczna długości podstaw * długość wysokości)
odjąć pola odpowiednich trójkątów i otrzymamy wynik
26 sie 16:31
Mariusz:
Mając ten stosunek oraz długość boku pole k można obliczyć
stosując twierdzenie cosinusów w tym 'niezaznaczonym trójkącie'
a następnie z jedynki trygonometrycznej obliczyć sinus
Obliczony sinus można wykorzystać do policzenia pola k
bo mamy kąty przyległe
wredulus pokazał jak policzyć długość boku więc zostaje jeszcze do pokazania
ten skąd kerajs wziął ten stosunek
26 sie 17:35
Mila:
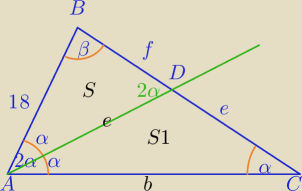
Zadanie 1)
|BC|=30
AD dwusieczna kąta A
1) ΔADB∼ΔABC cecha kkk
ΔADC−Δrównoramienny
2) Teraz można dalej na dwa sposoby
I ) z podobieństwa Δ z (1)
b=32
liczysz pole z wzoru Herona, to masz obliczone wyżej.
=====================================
albo
II) Liczysz pole Δ ADB z wzoru Herona
i potem korzystasz z własności
| S | | f | | 54 | | 96 | |
| = |
| = |
| : |
| =9:16 |
| S1 | | e | | 5 | | 5 | |
P
ΔABC=S+S
1
26 sie 17:38
Mariusz:
Co do pierwszego zadania to prawdopodobnie rozwiązałbym je tak jak wredulus
26 sie 17:49
chichi:
Ale Ty Mariusz utrudniasz wszystkie zadania... Wszystko na około

26 sie 18:01
Mariusz:
Rozwiązanie Mili też jest niezłe i dobrze skomentowany jest każdy jego krok
Ja po prostu prawdopodobnie prędzej bym wpadł na rozwiązanie wredulusa
gdybym samodzielnie miał to pierwsze zadanie rozwiązać
26 sie 18:05
chichi:
Ja mam na myśli Twoje komentarze odnośnie tego 2 zadania..

26 sie 18:07
Mila:
Cześć
Mariuszu.

Też mój pierwszy sposób byłby z zastosowaniem trygonometrii.
Jednak czasem uczniowie wolą rozw. bez trytgonometrii.
Jeżeli w trójkącie jeden z kątów jest dwa razy większy od .... to nasuwa się możliwość
skorzystania z dwusiecznej i z podobieństwa.
Może
Gabi kiedyś wykorzysta.
26 sie 18:07
chichi:
@
Mila a Ty jaki otrzymałaś wynik do zadania (2)

26 sie 18:09
chichi:
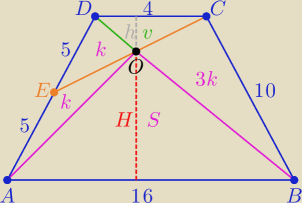
(1) k+v=9 ⇒ v=8−k
(2) v=0.5*4*h ⇒ v=2h
| | 8−k | |
Z (1) i (2) mamy, że: h= |
| |
| | 2 | |
| | 1 | | 8+k | |
(4) S= |
| *16* |
| =32+4k |
| | 2 | | 2 | |
P
ABCD=80=32+4k+k+3k+8 ⇒ k=5 ⇒
S=52 
26 sie 18:38
chichi:
k+v=8 **
26 sie 18:39
Mariusz:
k+v = 8 a to skąd wiemy
bez liczenia długości brakującego boku
poza tym to całkiem ładne rozwiązanie
Co do pomysłu kerajsa to
Może stąd, że pole niezaznaczonego trójkąta wynosi 8 j2, a jego najdłuższy bok liczący √65 j
dzielony jest przez wspólny wierzchołek trzech trójkątów w stosunku (od lewej) 5:3, co sprawia
iż k=5 j2.
Jeśli chodzi o długość boku EC to nie wpadłem na to aby dorysować trójkąt prostokątny
do boku ED
Na ten stosunek wspomniany przez kerajsa jednak nie mam pomysłu
Mając stosunek w jakim punkt O dzieli odcinek EC oraz długość odcinka EC
mógłbym obliczyć k z trygonometrii
Jeśli ty jej nie lubisz i masz zrozumiałe uzasadnienie bez trygonometrii to możesz je
przedstawić
26 sie 21:10
kerajs:
Niestety nie wpadłem na żadne szybkie rozwiązanie, a wrzucenie trapezu w układ współrzędnych
wydało mi się zbyt banalne.
Moje rozwiązanie jest siermiężne w stosunku do powyższego, więc niechętnie je piszę ulegając
pytaniu Mariusza:
'' zostaje jeszcze do pokazania ten skąd kerajs wziął ten stosunek''
Do oznaczeń jak na rysunku dwa posty wyżej dodałem oznaczenia: ∡EAO=α, ∡COD=β i |EO|=x
3P
AEO=P
BCO
| 3 | | 1 | |
| *5*x*sin(1800−β)= |
| *10*(√65−x)*sin(2α−β) |
| 2 | | 2 | |
| 3 | | 16 | | 1 | | 4 | | 4 | | 37 | |
| *5*x* |
| = |
| *10*(√65−x)*[2* |
| * |
| * |
| − |
| 2 | | 5√65 | | 2 | | 5 | | 5 | | 5√65 | |
| | 16 | | 9 | | 16 | |
|
| ( |
| − |
| )] |
| | 5√65 | | 25 | | 25 | |
| | 1 | | 5 | | 16 | |
PAEO=k= |
| *5* |
| √65* |
| =5 |
| | 2 | | 8 | | 5√65 | |
26 sie 21:16
kerajs:
26 sie 21:16
chichi:
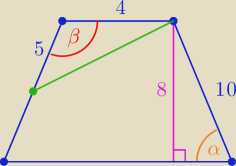
"k+v = 8 a to skąd wiemy
bez liczenia długości brakującego boku
poza tym to całkiem ładne rozwiązanie"
| | 4 | |
sinα = |
| = sinβ ( bo, β=180o−α, a sin(180o−α) = sinα ) |
| | 5 | |
Ten krok uznałem za zbyt oczywisty do opisania, ale tu masz wyjaśnienie

26 sie 21:17
chichi:
"Mając ten stosunek oraz długość boku pole k można obliczyć
stosując twierdzenie cosinusów w tym 'niezaznaczonym trójkącie'
a następnie z jedynki trygonometrycznej obliczyć sinus
Obliczony sinus można wykorzystać do policzenia pola k
bo mamy kąty przyległe"
Stąd mój wniosek, że chciałeś na około, bo zobacz jak łatwo dobieramy się do sinusa

26 sie 21:18
Mariusz:
Dobrze ale skąd wiemy że α+β=180° czyżby ten trapez można było wpisać w okrąg
kerajs , po odpowiedzeniu na moje pytania twój pomysł na
rozwiązanie staje się bardziej zrozumiały
Skąd długość brakującego boku
(To pytanie okazało się łatwe
po dorysowaniu trójkąta prostokątnego bo wtedy wystarczyło zastosować twierdzenie Pitagorasa)
Skąd ten stosunek
Jak wykorzystać stosunek i długość boku do obliczenia k
(Na początku nie miałem na to pomysłu ale gdy wredulus zaproponował dorysowanie
trójkąta prostokątnego i było zrozumiałe jak otrzymać długość boku zacząłem bawić
się trygonometrią i znalazłem sposób)
Ja chciałem rozwiązywać w tej kolejności co podałeś
we wpisie z 26 sie 10:36 i ciekaw byłem skąd otrzymałeś ten stosunek
w jakim punkt O dzieli odcinek EC (5:3)
Co do twojego wpisu z 26 sie 21:16 to jeszcze nie widzę skąd te kąty
przy sinusach
Tak , tak zgadzam się że rozwiązanie chichiego jest eleganckie i nawet dość zrozumiałe
No tak ja chciałem policzyć sinus innego kąta − przyległego do tego występującego w trójkącie
AEO bo chciałem wykorzystać pomysł kerajsa
26 sie 21:57
chichi:
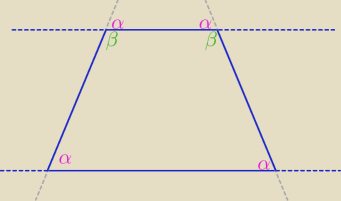
"Dobrze ale skąd wiemy że α+β=180° czyżby ten trapez można było wpisać w okrąg"
@
Mariusz mam wrażenie jakbyś w ogóle nie wiedział czym jest trapez...
"czyżby ten trapez można było wpisać w okrąg " − każdy trapez równoramienny można

26 sie 22:07
chichi:
Suma miar kątów wewnętrznych leżących przy tym samym ramieniu dowolnego trapezu jest równa 180°
26 sie 22:09
Mariusz:
trapez − czworokąt w którym przynajmniej jedna para boków jest równoległa
no teraz widać
No tak jak przetniemy kąt prostą równoległą to otrzymany w ten sposób kąt
będzie miał tę samą miarę
Tak właściwie to nie zaszkodzi rozbierać to zadanie do rzeczy które mogą wydawać się oczywiste
bo wtedy rozwiązanie będzie zrozumiałe nawet gdybyśmy chcieli wrócić do
rozwiązywania takich zadań po latach
26 sie 22:41
chichi:
Przecież to są podstawowe własności figur, które poznajemy już we wczesnych latach szkoły
podstawowej, czy uważasz, że rozwiązując zadanie np. z równoległobokiem należy pisać, że
przeciwległe boki są wzajemnie równoległe, czy to coś oczywistego?
26 sie 22:49
Mariusz:
Co do mnie to widać że mózg mi ostatnio zbyt dobrze nie pracuje a przecież
nie jestem jeszcze aż taki stary
26 sie 22:52
chichi:
Może to przemęczenie. Do geometrii, do tego kombinowania trzeba mieć świeży umysł

26 sie 22:55




 Mi amigo... widzę, że wyszło Ci , że |AC|=18, ale niestety należy to odrzucić, gdyż:
4x=180o ⇒ 2x=90o → ΔABC jest równoramienny, prostokątny, zatem |BC|=18√2≠30 SPRZECZNE!
Mi amigo... widzę, że wyszło Ci , że |AC|=18, ale niestety należy to odrzucić, gdyż:
4x=180o ⇒ 2x=90o → ΔABC jest równoramienny, prostokątny, zatem |BC|=18√2≠30 SPRZECZNE!


 @wredulus−pospolitus coś dorysować i... korzystam z takich trójkącików i mam, że:
@wredulus−pospolitus coś dorysować i... korzystam z takich trójkącików i mam, że:
 (k=3√11 oraz h=5√11)
(k=3√11 oraz h=5√11) No to ja poszedłem całkowicie inną drogą, czyli bawiłem się trygonometrią:
wychodzimy z tw. sinusów:
No to ja poszedłem całkowicie inną drogą, czyli bawiłem się trygonometrią:
wychodzimy z tw. sinusów:



 @gabi03 czytasz w ogóle nasze posty? Wyjaśniłem Ci wyżej, jak wyeliminować odpowiedź
|AC|=18... można to zrobić też tak:
@gabi03 czytasz w ogóle nasze posty? Wyjaśniłem Ci wyżej, jak wyeliminować odpowiedź
|AC|=18... można to zrobić też tak:



 (18+32+30)/2
(18+32+30)/2  (wcześniej też napisałaś h/36cosx zamiast h/(36cosx) )
Wierz mi −−− to jest ogromna różnica
(wcześniej też napisałaś h/36cosx zamiast h/(36cosx) )
Wierz mi −−− to jest ogromna różnica 
 Z podobieństwa trójkątów równoramiennych DBC i DAB
Z podobieństwa trójkątów równoramiennych DBC i DAB





 , @gabi03 nad oknem pisania w prawym górnym rogu rysuję
, @gabi03 nad oknem pisania w prawym górnym rogu rysuję 

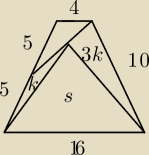 Polecenie to tylko Wyznacz S.
Polecenie to tylko Wyznacz S.
 P.S. Zakładaj nowe posty, jeśli wstawiasz nowe zadanie
P.S. Zakładaj nowe posty, jeśli wstawiasz nowe zadanie 


 stąd wziął x2 = 42 + 72
stąd wziął x2 = 42 + 72
 Zadanie 1)
|BC|=30
AD dwusieczna kąta A
1) ΔADB∼ΔABC cecha kkk
Zadanie 1)
|BC|=30
AD dwusieczna kąta A
1) ΔADB∼ΔABC cecha kkk


 Też mój pierwszy sposób byłby z zastosowaniem trygonometrii.
Jednak czasem uczniowie wolą rozw. bez trytgonometrii.
Jeżeli w trójkącie jeden z kątów jest dwa razy większy od .... to nasuwa się możliwość
skorzystania z dwusiecznej i z podobieństwa.
Może Gabi kiedyś wykorzysta.
Też mój pierwszy sposób byłby z zastosowaniem trygonometrii.
Jednak czasem uczniowie wolą rozw. bez trytgonometrii.
Jeżeli w trójkącie jeden z kątów jest dwa razy większy od .... to nasuwa się możliwość
skorzystania z dwusiecznej i z podobieństwa.
Może Gabi kiedyś wykorzysta.

 (1) k+v=9 ⇒ v=8−k
(2) v=0.5*4*h ⇒ v=2h
(1) k+v=9 ⇒ v=8−k
(2) v=0.5*4*h ⇒ v=2h

 "k+v = 8 a to skąd wiemy
bez liczenia długości brakującego boku
poza tym to całkiem ładne rozwiązanie"
"k+v = 8 a to skąd wiemy
bez liczenia długości brakującego boku
poza tym to całkiem ładne rozwiązanie"


 "Dobrze ale skąd wiemy że α+β=180° czyżby ten trapez można było wpisać w okrąg"
@Mariusz mam wrażenie jakbyś w ogóle nie wiedział czym jest trapez...
"czyżby ten trapez można było wpisać w okrąg " − każdy trapez równoramienny można
"Dobrze ale skąd wiemy że α+β=180° czyżby ten trapez można było wpisać w okrąg"
@Mariusz mam wrażenie jakbyś w ogóle nie wiedział czym jest trapez...
"czyżby ten trapez można było wpisać w okrąg " − każdy trapez równoramienny można 
