trygonometria Dexter: Niech a,b,c∊R. Warunkiem koniecznym i wystarczającym, aby dla każdego x∊R ,asin x+bcosx+c>0 jest a)a=b=0,c>0 b)√a²+b²=c c)√a²+b²<c d)√a²+b²>c

chichi: To jakiś egzamin poprawkowy?

Dexter: Tak, przygotowanie

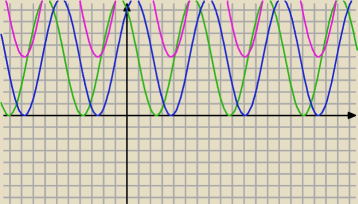
a7: powyżej wykres y=−3sinx+4cosx+5 wyklucza b a=b=0, c>0 jest warunkiem wystarczajacym, ale nie koniecznym więc wykluczam a (wykres fioletowy y=3sinx +4cosx+10))

a7: obstawiam c

wredulus_pospolitus: (a) odpada, bo to nie jest z pewnością warunek konieczny, (niech a=0 , b = 1 , c = 2 i nierówność spełniona) (b) biorąc te same a,b,c co powyżej −−− odpada (d) biorąc te same a,b,c co powyżej −−− odpada więc ostaje się tylko (c)

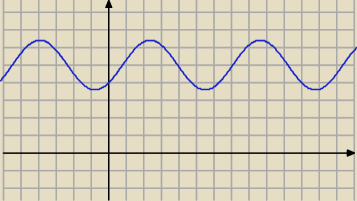
a7: powyżej wykres y=sinx−cosx+5

Dexter: A da się jakośc dojść do teg bez wyboru przykładów?

Dexter: Jakby było np uzasdnij że c) ?

a7: no tak sposób wredulusa lepszy − na egzaminie nie ma pewnie kalkulatora do wykresów

a7: 16:19 ale nie wystarczy metoda selekcji? że nie a nie b i nie d

a7: no weżmy minimum jakie może przyjąć ta funkcja dla √a²+b²=c² i mamy uzasadnienie

a7: =c

ICSP: asinx + bcosx + c > 0 √a² + b²sin(x + α) + c > 0 będzie prawdziwe dla dowolnego x ∊ R gdy √a² + b² < c Czyli odpowiedź c)

a7: liczymy pochodną a,b,c to stałe i mamy uzasadnienie (?)

wredulus_pospolitus: @ICPS ... proponuję wyjaśnić skąd ten wzór wziąłeś

ICSP: https://matematykaszkolna.pl/forum/94007.html Vax − 12 maj 17:30

Mila: f(x)=a*sin x+b*cosx https://en.wikibooks.org/wiki/Trigonometry/Simplifying_a_sin(x)_%2B_b_cos(x)