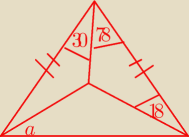
geometria trojkata adrianeek: wyznacz miare kata a

chichi: a=24^o, niestety moje rysunki nie mieszczą się na obszarze roboczym Może ktoś inny wrzuci rozwiązanie

Mariusz: adrianek mogłeś jakoś nazwać te wierzchołki Można by wyznaczyć brakujące kąty (z tego że mamy trójkąt równoramienny oraz z sumy kątów w trójkącie) a następnie z twierdzenia sinusów Miary kątów w tych trójkątach to 108° , 36°, 36° a , 18° 162° − a 78°,18°,84° 30°, 36° − a,114°+a

x		y
	=
sin(114°+a)		sin(36° − a)

x		y
	=
sin(84°)		sin(18°)

x		sin(114°+a)
	=
y		sin(36° − a)

x		sin(84°)
	=
y		sin(18°)

sin(114°+a)		sin(84°)
	=
sin(36° − a)		sin(18°)

sin(180°−(114°+a))		sin(84°)
	=
sin(36° − a)		sin(18°)

sin(66°− a)		sin(84°)
	=
sin(36° − a)		sin(18°)

sin(30°+(36°−a))		sin(84°)
	=
sin(36° − a)		sin(18°)

1	cos(36°−a)		√3	sin(36°−a)		sin(84°)
		+			=
2	sin(36° − a)		2	sin(36°−a)		sin(18°)

1	sin(90°−(36°−a))		√3	sin(36°−a)
		+
2	cos(90°−(36° − a))		2	sin(36°−a)

	sin(84°)
=
	sin(18°)

1	sin(54°+a)		√3		sin(84°)
		+		=
2	cos(54°+a)		2		sin(18°)

sin(54°+a)		sin(84°)
	=2		−√3
cos(54°+a)		sin(18°)

	sin(84°)
tg(54°+a) = 2		−√3
	sin(18°)

sin(84°)=cos(6°)

	√3		1
cos(6°)=cos(36°−30°)=		cos(36°)+		sin(36°)
	2		2

	√3(√5+1)		√10−2√5		4
tg(54°+a) = (		+		)		−√3
	4		4		√5−1

	√15+√3+√10−2√5
tg(54°+a) =		−√3
	√5−1

	√5+1
tg(54°+a) = (√15+√3+√10−2√5)		−√3
	4

	√75+√15+√50−10√5+√15+√3+√10−2√5−4√3
tg(54°+a) =
	4

	2√3+2√15+√50−10√5+√10−2√5
tg(54°+a) =
	4

Lepiej by było po prawej stronie dojść do wzoru na tangens sumy np tg(60°+18°) no ale cóż można tę wartość wyszukać w tablicach

adrianeek: Czyli trzeba znalezc przyblizona wartosc tej liczby z prawej strony rownania a pozniej przyblizona wartosc kata w tablicach?

Kacper: Skąd to zadanko?

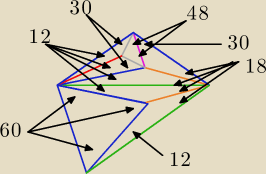
chichi: Czysta geometria → a=24^o

Mariusz: "Czyli trzeba znalezc przyblizona wartosc tej liczby z prawej strony rownania a pozniej przyblizona wartosc kata w tablicach?" Wtedy będziesz miał wynik przybliżony Może dać ci przypuszczenie że należy spróbować prawą stronę porównać ze wzórem na tangens sumy tg(60°+18°) Trzeba sprawdzić czy prawdziwa jest równość

√25−10√5   √3+   5
	=
√25−10√5   1−√3   5

2√3+2√15+√50−10√5+√10−2√5
4

Mariusz: Uwagi do tego w jaki sposób można wykazać tę równość Po usunięciu z niewymierności z mianownika po lewej stronie równania redukujesz wyrazy podobne a następnie mnożysz równanie przez taki czynnik by po lewej stronie uzyskać wzór na różnicę kwadratów Po prawej stronie po wymnożeniu wyrażenia podpierwiastkowe należy zapisać w postaci zupełnych kwadratów

www: tu podobne: https://math.stackexchange.com/questions/245608/find-an-angle-in-a-given-triangle

a7: ja chyba rozumiem co tam chichi napisał, po pierwsze tam gdzie jest podstawa (nazwijmy ją AB) i kąty x i 2x dorysowujesz trójkąt o kącie 36 i ramieniu BA'. po drugie łączysz A i A' oraz rysujesz trójkąt równoboczny na podstawie AA' i łączysz jego wierzchołek (powiedzmy B') z B teraz widzisz, że masz tam trójkąty równoramienne m. innymi ten z pomarańczowymi ramionami, wyliczasz potrzebne kąty i wychodzi, że a=24^o

Mariusz: "ja chyba rozumiem co tam chichi napisał, po pierwsze tam gdzie jest podstawa (nazwijmy ją AB) i kąty x i 2x dorysowujesz trójkąt o kącie 36 i ramieniu BA'." Gdzie ty widzisz podstawę z kątami x i 2x a na oryginalnym rysunku do tego zadania masz trójkąt równoramienny podzielony na trzy trójkąty

chichi: @a7 pomyliła chyba z rysunkiem z tego zadania https://matematykaszkolna.pl/forum/410989.html

www: Tu w pierwszym poście jest fajny sposób, może ktoś wykorzysta do tego zadania: https://math.stackexchange.com/questions/2613282/triangle-abc-has-ac-bc-and-angle-acb-96-circ-d-is-a-point-such-that?rq=1

chichi: Rozwiązałem też w ten sposób, ale co nieco jeszcze trzeba było dorysować, może później wrzucę

Mariusz: A możliwe że a7 pomyliła rysunki www jak sam widzisz tam rysunki są tylko ilustracją dla rozwiązania i oprócz tego lepiej lub gorzej opisany sposób rozwiązania zadania natomiast chichi wrzuca tylko rysunki Wprawdzie są dobrze opisane ale to tylko rysunki i ci którym mogłyby one się przydać na ogół nie będą wiedzieć dlaczego te rysunki zostały akurat tak opisane Można by się też się zastanowić dla kogo chichi te rysunki wrzuca "Dla tych którzy wiedzą co to jest "pięć" w geometrii " − no cóż oni raczej tych rysunków nie potrzebują Dla siebie − chyba raczej też nie

chichi: @Mariusz to, że trójkąt równoboczny ma wszystkie kąty równej miary, a trójkąt równoramienny kąty przy podstawie równej miary, to chyba każdy wie co? Nie widzę sensu pisać pod rysunkiem, że 96^o:2=48^o czy też sumowanie do 180^o. Cała trudność to skonstruowanie takiego rysunku, w przytoczonym przykładzie tam tego też nikt nie opisuje.. To po prostu geometria syntetyczna

adrianeek: dziekuje za wszystkie rozwiazania musze jeszcze pocwiczyc takie dorysowywanie roznych odcinkow i trojkatow

www: rozumiesz to rozwiązanie chichi, bo ja nie

adrianeek: sam rysunek i uzupelnienie katow tak ale nie zrobilbym takiego rysunku trzeba kreatywnosci dlatego bede probowal robic podobne triki w zadaniach takiego typu bo jeszcze pare mam podobnych moze wrzuce swoje rozwiazanie do jakiegos innego w tym watku jak mi sie uda dlatego prosze administracje zeby nie zamykala tego watku dziekuje

adrianeek: na poczatku probowalem tak jak Mariusz ale wychodza takie rownania ze doszedlem do wniosku ze nie tedy droga i chyba trzeba takie kombinacje robic do rozwiazania

www: adrainek zrób lepszy rysunek jak rozumiesz z objaśnienami

www: I jak, zrobisz?

adrianeek: www nie bede robil nowego rysunku bo tu przeciez widac. wychodze z domu wiec jutro po poludniu moge sprobowac ci wyjasnic, tylko napisz czego nie rozumiesz

www: np gdzie jest ten wyjściowy trójkąt bo nawet tego tam nie widzę

www: Miałeś wyjaśnić. Może zrób tak jak w tym zadaniu: 1. AD = BC 2. ∠BCD = 42 ° 3. ∠ABC = 84 ° Wyznacz wartość ∠A https://www.szybkiplik.pl/hoBKhH9tFa