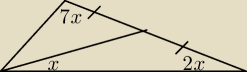
zadanie matma: Oblicz miarę kąta x. Z twierdzenia sinusów dochodzę do dość skomplikowanego równania.

chichi: x=15^o

matma: mam odpowiedz ale chodzi mi o sposób

chichi: Rozwiązałem w notesie w aucie, jak wrócę do domu to wrzucę

matma: ok poczekam

Mariusz: Skorzystajmy jak proponujesz z tw sinusów

a		s
	=
sin x		sin 2x

a		s
	=
sin(180 − 10x)		sin 7x

a		sin x
	=
s		sin 2x

a		sin(180 − 10x)
	=
s		sin 7x

a		sin x
	=
s		sin 2x

a		sin 10x
	=
s		sin 7x

sin x		sin 10x
	=
sin 2x		sin 7x

sin(x)sin(7x)=sin(2x)sin(10x) 2sin(x)sin(7x)=2sin(2x)sin(10x) cos(α+β)=cos(α)cos(β)−sin(α)sin(β) cos(α−β)=cos(α)cos(β)+sin(α)sin(β) 2sin(α)sin(β) =cos(α−β)−cos(α+β) cos(6x)−cos(8x)=cos(8x)−cos(12x) cos(12x)−2cos(8x)+cos(6x)=0 cos((n+1)x)=cos(nx)cos(x)−sin(x)sin(nx) cos((n−1)x)=cos(nx)cos(x)+sin(x)sin(nx) cos((n+1)x)+cos((n−1)x)=2cos(x)cos(nx) cos((n+1)x)=2cos(x)cos(nx)−cos((n−1)x) T_n+1=2xT_n−T_n−1 , n ≥ 1 T₀ = 1 T₁ = x T₂ = 2x² − 1 T₃ = 2x(2x² − 1)−x T₃ = 4x³ − 3x T₄ = 2x(4x³−3x)−(2x²−1) T₄ = 8x⁴−8x²+1 T₅ = 2x(8x⁴−8x²+1)−(4x³ − 3x) T₅ = 16x⁵ − 16x³+2x − 4x³ + 3x T₅ = 16x⁵ − 20x³+5x T₆ = 2x(16x⁵ − 20x³+5x)−(8x⁴−8x²+1) T₆ = 32x⁶−40x⁴+10x² − 8x⁴ + 8x² − 1 T₆ = 32x⁶ − 48x⁴ + 18x² − 1 cos(12x)−2cos(8x)+cos(6x)=0 t = cos(2x) (32t⁶ − 48t⁴ + 18t² − 1)−2(8t⁴−8t²+1)+4t³ − 3t = 0 32t⁶ − 64t⁴ + 4t³ + 34t² − 3t − 3 = 0 8t⁴(4t²−3)−10t²(4t²−3)+(4t²−3)+t(4t²−3)=0 (4t²−3)(8t⁴−10t²+t+1)=0

matma: Mariusz bardziej chodziło mi aby tego uniknąc

matma: chichi i jak?

Kacper: Jakie jest źródło tego zadania?

chichi: @matma spójrz w link poniżej i spróbuj załatwić sprawę w podobny sposób https://matematykaszkolna.pl/forum/411000.html

matma: trochę za duzo strzałek, nic nie rozumiem

chichi: Strzałki idą tylko do kątów, niestety nie da się inaczej, na rysunku tym bardziej bym ich nie podpisał..

matma: może w innym programie a tu umieść link

matma: https://foto-hosting.pl/img/c4/dc/91/c4dc915d276c960dbe23aa38b6c3a60167bf18fd.jpeg Okrąg opisany na czworokącie...