Podobieństwo figur KaKaKa: Witam, mam problem z następującym dowodem: W trapezie ABCD o podstawie AB przez punkt O przecięcia przekątnych prowadzimy dwie proste równoległe do boków BC i DA, przecinające podstawę AB odpowiednio w punktach A′ i B′. Udowodnij, że |AA′|=|BB′|. https://www.linkpicture.com/q/tr_2.png (pod linkiem grafika do zadania) Doszłam do tego, że trójkąty DD′O i BB′O oraz trójkąty AA′O i CC′O są podobne. Nie bardzo wiem jak to pociągnąć dalej. Domyślam się, że w pewnym momencie trzeba będzie przyrównać do siebie obie skale podobieństwa ale nie potrafię zargumentować dlaczego. Proszę o pomoc i dziękuję

chichi: No i super, zauważ również, że czworokąty AB'D'D oraz BA'C'C to równoległoboki, więc odpowiednie długości są sobie równe. Skorzystaj z podobieństwa i się samo rozwiązuje

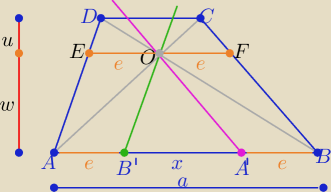
Maja: 1/ wykażemy,że odcinki EO| i |OF| mają równe długości trójkąty ABD i DEO i trójkaty ABC i COF są podobne z cechy (kkk)

	a		w+u		a		w+u
to		=		i		=
	|OE|		u		|OF|		u

więc |OE|=|OF|=e = |AB^'|=|A^'B| i mamy tezę: |AA^'|= e+x , |BB^'|= x+e więc |AA^'|=|BB^'| c. n.w.

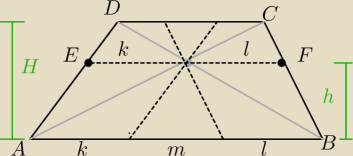
wredulus_pospolitus: de facto masz wykazać, że k = l (bo 'm' występuje w obu odcinkach: |AA'| oraz |BB'| więc można go pominąć) najłatwiej będzie to wykazać poprzez wykazanie, że P_{Δ AB'O} = P_{Δ BA'O}. Albo nie ... prowadzimy równoległą do podstaw, przechodzącą przez punkt O. |EO| = |AB'| = k (równoległe w równoległoboku mają taką samą długość) oraz |OF| = |A'B| = l z podobieństwa trójkątów AEO i ADC mamy:

k		hΔAEO		h
	=		=
|DC|		hΔACD		H

z podobieństwa trójkątów BFO i BDC mamy:

l		hΔBFO		h
	=		=
|DC|		hΔBCD		H

	k		l
stąd:		=		−−−> k = l
	|DC|		|DC|

więc |AA'| = k+m = l+m = |BB'| c.n.w.

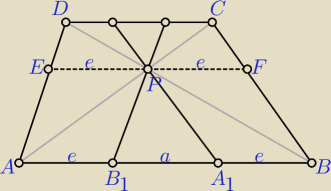
Gucio: Najpierw trzeba pokazać, że |EP| =|PF| = e i dalej jest już prosto

Gucio:

Maja:

wredulus_pospolitus: hmmm hmmm hmmm

Maja: mmmh mmmh mmmh

Maja: Wredulus widziałeś te 5 równań z 5−oma niewiadomymi https://matematykaszkolna.pl/forum/410176.html

wredulus_pospolitus: widziałem ... kompletnie tam dałem ciała ... nawet nie zauważyłem trójkąta 3:4:5 tworzonego przez środki okręgów tylko pisałem że jest to 7r:9r:c no i później zacząłem szukać kolejnych równań i tak wyszło 5 równań ze złą proporcją

wredulus_pospolitus: no i przedewszystkim źle przeczytałem treść zadania i myślałem, że chodzi o wyznaczenie (wprost) promienia tych małych okręgów

Maja: