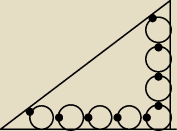
trójkat 16: Dany jest trójkąt prostokątny oraz 8 jednakowych okregów o promieniu r stycznych do boków trójkąta oraz stycznych do siebie tak jak na rysunku. Oblicz promień okręgu wpisanego w dany trójkat prostokątny.

wredulus_pospolitus: nie ma kompletnie żadnej informacji co do tego jaki to jest trójkąt prostokątny

16: Tylko tyle że prostokatny.

Maja: Prostokątny o ramionach różnej długości to chyba widać z rysunku wredulusie

wredulus_pospolitus: mam wizję jak to rozwiązać, ale to rozwiązanie polega na rozwiązaniu układu 5 równań z 5cioma niewiadomymi z czego jedną z nich jest funkcja trygonometryczna (do wyboru do koloru która) i szczerze mówiąc to patrząc na ten układ odechciewa mi się to liczyć. Nie wiem ... może ktoś ma jakiś łatwy sposób na policzenie tego

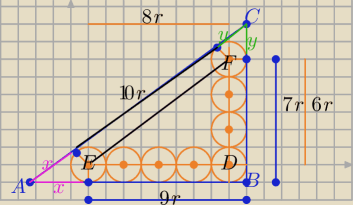
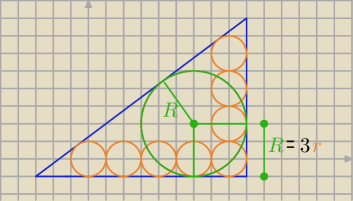
Maja: W ΔEDF : |ED|=8r , |DF|=6r to |EF|= 10r W ΔABC : |AB|= 9r+x , |BC|= 7r+y , |AC|= 10r+x+y to 2R= 9r+x+7r+y−10r−x−y 2R= 6r R= 3r , R− dł. promienia okręgu wpisanego w ΔABC =====

Maja: