dowód Mat: Na bokach AB i AD rombu ABCD wybrano odpowiednio punkty M i L w ten sposób, że |AL | = |AM | = 3/5|AB | . Odcinek LM jest styczny do okręgu wpisanego w romb ABCD . Punkt K jest punktem styczności okręgu wpisanego w ten romb z bokiem AD (zobacz rysunek). Wykaż, że |AK|/|KD| = 21/4 https://img.zadania.info/zes/0053818/HzesR122x.gif

ite: a na zadania.info jest tylko rysunek? nie ma rozwiązania?

Mat: Brak

Czas kosić trawniki: Pewnie rozwiązanie jest dla użytkowników z wykupionym abonamentem Drogi teraz jest?

chichi: https://matematykaszkolna.pl/forum/409005.html − 12 kwietnia 21:03

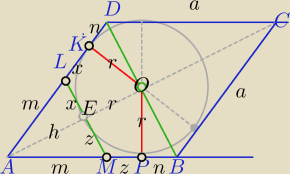
Mila: Punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta

	3
m=		a
	5

1) ΔAEL∼ΔAOD⇔

m		a		5
	=		⇔|OD|=		x
x		|OD|		3

	h		h+r		3
ΔAEL∼ΔAOD⇔		=		⇔h=		r
	x		(5/3x)		2

	5
|AO|=		r
	2

2) W ΔAKO:

	5		21
(		r)2=|AK|2+r2 ⇔|AK|2=		r2
	2		4

	√21
|AK|=		r
	2

=========== 3) W ΔAOD:

	√21
r2=|AK|*n ⇔r2=		r*n
	2

	2r
n=
	√21

=========== 4}

|AK|		√21r   2
	=
|KD|		2r   √21

|AK|		21
	=
|KD|		4

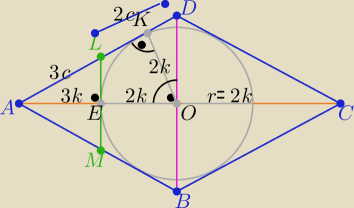πesio: To jeszcze taki sposób Wprowadzam r= 2k >0 ( bardziej "przyjazne" będą obliczenia Z tw. Talesa w ΔAOD : |AE|=3k, |EO|=2k to |AO|=5k i z tw. Pitagorasa w ΔAOD : |AK|²=(5k²)−(2k)² ⇒ |AK|²=21k² oraz (2k)²=|AK|*|KD| ^2

	16k2
to 16k4=|AK|2*|KD|2 ⇒ 16k4=21k2*|KD|2⇒ |KD|2=
	21

	|AK|		21k2*21		21
więc: (		)2=		=(		)2
	|KD|		16k2		4

	|AK|		21
to		=
	|KD|		4

===========

Mila: A gdzie rozwiązanie πqś−a ?