Zadania maturalne PR i PP
Damian#UDM: Zadania maturalne PR i PP
Dzień dobry kochani

Chciałbym wam życzyć miłego wieczoru i kolejnych dni

A teraz zadania z matmy.
https://pdf.zadania.info/94253.pdf − rozwiązuje ten arkusz i mam problem z zadaniami: 6, 13 oraz 14.
W zadaniu 6. i 14. nie mam pomysłu.
W zadaniu. 13. nie wiem jak policzyć długości odcinków BF oraz BD, dzięki czemu mógłbym
skorzystać z twierdzenia cosinusów w trójkącie BFD.
Proszę o pomoc

12 kwi 19:40
wredulus_pospolitus:
14.
Skoro wierzchołki A i B są odległe o 5
√5 od punktu K, oraz o 25 od punktu L, to znaczy że ich
współrzędne wyznaczyć poprzez rozwiązanie układu równań:
| ⎧ | równanie okręgu o środku K i promieniu 5√5 | |
| ⎩ | równanie okręgu o środku L i promieniu 25 |
|
12 kwi 19:45
blabla:
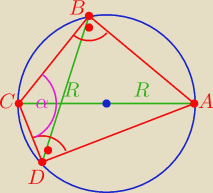
W 6 ? ( łatwizna)
|CD|=2R
z tw. sinusów w ΔBCD
sinα= 10/13
i po ptokach

12 kwi 19:51
chichi:
| | 20 | |
|AC|=2R ∧ |AC|=1.3|BD| ⇒ |BD|= |
| R |
| | 13 | |
Z tw. sinusów w ΔBCD:
| |BD| | | | | 10 | |
| =2R ⇒ |
| =2R ⇒ sin(α)= |
| |
| sin(α) | | sin(α) | | 13 | |
12 kwi 19:58
chichi:
Cześć @
blabla jak zwykle się spóźnię, ale dużo czasu zajmuje mi zrobienie dobrego rysunku,
a skąd u Ciebie moja droga |CD|=2R ?

12 kwi 20:00
chichi:
Z tej równości wynikałoby jako, że długość przyprostokątnej jest równa długości
przeciwprostokątnej

12 kwi 20:01
blabla:
AC miało byc

12 kwi 20:04
12 kwi 20:06
blabla:
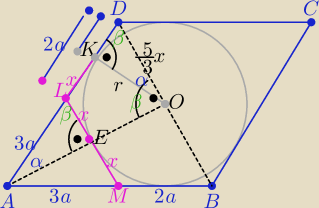
Np: tak
|KD|=2a−x , |AK|=3a+x , x∊(0,2a) x −−− z tw. o odcinkach stycznych
| | 5 | |
|OD|= |
| x ( z podobieństwa ΔAEL i ΔAOD |
| | 3 | |
i z podobieństwa ΔAOD i ΔKOD
| | a | | x | | a | |
2( |
| )−1= (5/9)* |
| /*( |
| >0 |
| | x | | a | | x | |
2(a/x)
2−(a/x)−(5/9) =0 Δ= 49/9
==========
12 kwi 21:03
blabla:
Ładne zadanko

12 kwi 21:05
Damian#UDM: O ludzie, 10. zadanie akurat udało mi się samemu ogarnąć

Skorzystałem tylko z podobieństwa
trójkątów oraz tw. o odcinkach stycznych i doszedłem do takiej samej równości

zadanie za 4
punkty, a tyle liczenia.
Arkusze maturalne z zadania.info powinny być na 70 a nie 50 punktów
 wredulus
wredulus świetny pomysł, nigdy bym na to nie wpadł

Rozwiąże je w ten sposób sam.
6. zadanie robiłem podobnie z twierdzenia sinusów lecz nie znalazłem żadnego powiązania między
wartościami

No i zostało zadanie 13. zapraszam do pomagania

12 kwi 21:10
Damian#UDM: Dziękuję wam, jesteście super

Zawsze można na was liczyć.
Fajnie, że tutaj jesteście

12 kwi 21:11
Damian#UDM: Co do zadania 13. to widziałem kiedyś coś takiego jak rombodeltoid i to była bryła trochę
podobne do tej w zadaniu 13.
12 kwi 21:12
blabla:
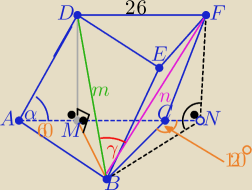
Z treści zadania w ΔAMD |DM=24 i AM=10
ΔAMD ≡ ΔCNF to NF=24 i CN=10
z tw. cosinusów w ΔBAM wyznacz BM
2
i z tw. Pitagorasa w ΔDMB m
2
analogicznie z drugiej strony
w ΔBCN wyznacz BN
2 (
i z Pitagorasa w ΔBNF n
2
i już z górki
| | m2+n2−262 | |
cosγ = |
| =.............. |
| | 2mn | |
nie chc mi się tego liczyć

12 kwi 21:43
Damian#UDM: Już dalej sobie ogarnę, dziękuję

12 kwi 21:45
blabla:

12 kwi 21:46
chichi:
| | 39√651 | |
Otrzymałem w zad. 13 cos(∡DBF)= |
| dosyć brzydki wynik, daj znać co Ci wyszło po |
| | 1302 | |
obliczeniu, a w zad. 14 mam, że A=(5,5) B=(−2,6) C=(1,−3) bądź C=(121,−3)

13 kwi 01:07
urban:
| | 39√651 | |
Ja też w zadaniu 13 otrzymałem wynik |
| , ale w zadaniu 14 mam inny |
| | 1302 | |
wynik dla C
13 kwi 11:58
chichi:
Sprawdzałem wszystko w GeoGebrze, szukaj u Siebie błędu, jeśli nie możesz znaleźć to wstaw
rozwiązanie tutaj, to zerknę

13 kwi 13:14
blabla:
Zad 14
Potwierdzam odp podaną przez chichi
A(5,5) , B(−2,6) C(1,−3) lub C(121,−3)
==============================
13 kwi 14:12
urban:
C = (1, − 3) oraz C = (121, −3), przepraszam

13 kwi 16:51
nabru:

13 kwi 19:28
Damian#UDM: Jak obliczyć współrzędne punktu C?
Głowię się nad tym i nie mam pojęcia

15 kwi 23:27
15 kwi 23:28
Damian#UDM: Trudna ta matura. Przy tych zadaniach czuje się jak debil.
15 kwi 23:30
Damian#UDM: Punkty K i L też leżą na symetralnej odcinka AB ?
15 kwi 23:32
Damian#UDM: No właśnie myślałem o podobnej kwestii, że trójkąt ten jest równoramienny, lecz tak nie jest. A
teraz widzę o co chodzi. Dziękuję

15 kwi 23:33
Damian#UDM: https://drive.google.com/drive/folders/1aksH8EaMHyhJp8BzAMwfT45tTc2xBPGe?usp=sharing
Zostawiam tutaj link do matury, z którą mam problem. A mianowicie:
Zadanie 15. (0−7) − nie wiem jak wyznaczyć wzór na to pole czworokąta.
Zadanie 14. (0−6) − nie wiem jak wyznaczyć wysokość i obliczyć cokolwiek w tym przekroju.
Jeśli ktoś ma ochotę to może zerknąć na zadanie 8. − jeszcze się za nie nie zabierałem.
Dziękuje wam za pomoc i serdecznie pozdrawiam was

16 kwi 01:37
chichi:
Trzeba wysyłać jakąś prośbę o dostęp lol
16 kwi 01:38
Saizou :
Kolega nie zmienił uprawień dostępu. Pewnie udostępnił, ale bez możliwości przeglądania.
16 kwi 09:47
chichi:
Nie wiem dlaczego tak trudno przepisać polecenia, aż takie lenistwo?

16 kwi 09:49
Philips: przekopiować*
16 kwi 10:21
16 kwi 11:23
ite: To jest troska o to, żeby praca włożona we wpisane rozwiązania była dostępna dla wszystkich
użytkowników tego forum i na długo.
Rozwiązanie bez dostępnej treści nic nikomu nie da, jeśli przestaniesz za kilka dni udostępniać
swój dysk, to nie będzie wiadomo, o co komu chodziło.
Ludzie szukający pomocy wpisują (również w googlach) treść zadania, więc nikt ni trafi do tego
rozwiązania.
16 kwi 11:33
Damian#UDM: Wszystko rozumiem

Pozdrawiam was
16 kwi 11:49
och&ach:
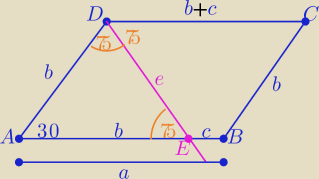
Należy wykazać,że e=2c
z treści zadania:
| b+c | | 2+√2−√3 | |
| = |
| ⇒ 2c=b√2−√3 |
| b | | 2 | |
z tw. cosinusów w ΔAED
e
2=.................
e=b
√2−√3
e=2c
16 kwi 12:17
chichi:
Zadanie 8 można też z tw. sinusów udowodnić, lecz sposób podany przez @
Eta jest szybszy

16 kwi 12:26
chichi:
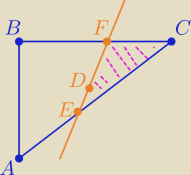
Zad. 15 Zauważmy z rysunku, że pole czworokąta ABFE będzie największy, kiedy pole trójkąta EFB
będzie najmniejsze, dalej już łatwo

16 kwi 12:33
chichi:
W zadaniu 14 wysokość można wyznaczyć z tw. Pitagorasa

16 kwi 12:37
och&ach:

16 kwi 12:43
chichi:
@
Eta ja otrzymałem V=144
√3, szukałem błędu rachunkowego i nie widzę, zerknij u Siebie

16 kwi 13:35
chichi:
U mnie w ogóle przekrój jest pięciokątem, nie sześciokątem

16 kwi 13:36
och&ach:
Ja źle zapamiętałam treść ( ukrytą w linku)
Ty masz dobrze
Tak , to jest jak autorowi postu nie chce się przepisać zadania !
16 kwi 16:46
och&ach:
Sorry ..... i po ptokach

16 kwi 16:49
Saizou :
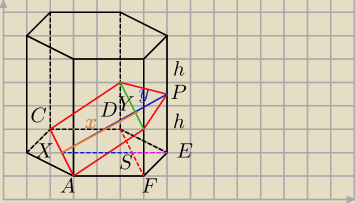
AC =4
√3
Z informacji o polu mamy, że
| | 1 | |
10√15 = 4√3x + |
| *4√3y ⇒ 2x + y = 5√5 (1) |
| | 2 | |
XS = 4
SE = 2
ΔXSY ~ΔXEP (kkk)
Łącząc informacje (1) oraz (2) mamy, że x = 2
√5, y =
√5
Z tw. Pitagorasa w PXE
h
2 + 6
2 = (3
√5)
2 → h = 3
16 kwi 16:58
och&ach:

16 kwi 17:35
Damian#UDM: Każdy popełnia błędy, nie ma co za to obwiniać innych

8. (0−3) PR
| | |AB| | | 2+√2−√3 | |
Kąt ostry BAD równoległoboku ABCD ma miarę 30 stopni, oraz |
| = |
| . |
| | |AD| | | 2 | |
Dwusieczna kąta wypukłego ADC przecina bok AB w punkcie E. Uzasadnij, że w czworokąt EBCD
można wpisać okrąg.
14. (0−6) PR
Graniastosłup prawidłowy sześciokątny, w którym krawędź podstawy ma długość 4, przecięto
płaszczyzną zawierającą krótszą przekątną podstawy AC oraz punkt P, który jest środkiem
krawędzi bocznej EE' (rysunek obok). Oblicz objętość graniastosłupa, jeśli pole przekroju jest
równe 10
√15.
15. (0−7) PR
Dany jest trójkąt ABC, gdzie A=(1,2) B=(1,10) C=(9,10). Przez punkt D=(5,7) poprowadzono prostą
o współczynniku kierunkowym dodatnim, która przecina boki AC i BC trójkąta odpowiednio w
punktach E oraz F. Wyznacz współrzędne punktów E i D, dla których pole czworokąta AEFB jest
największe.
Proszę bardzo, specjalnie dla was

Żeby nikt już nie popełniam więcej niepotrzebnych błędów
przez ukryte treści

.
16 kwi 18:24
Damian#UDM: A ja nadal nie wiem jak zrobić zadanie 15. Mam niewiadomą współczynnik prostej a oraz x i nie
zrobię z tego funkcji jednej zmiennej.
E=F=(x,ax+7−5a), oraz F=(x,10)
y−10=0
|CF|=9−x
h
ΔEFC=|ax−5a−3|
16 kwi 18:30
chichi:
| | 5a−6 | | 6a−7 | | 5a+3 | |
E=( |
| , |
| ) ∧ F=( |
| , 10) |
| | a−1 | | a−1 | | a | |
16 kwi 18:33
chichi:
O ile nie mam błędu rachunkowego oczywiście

16 kwi 18:34
Damian#UDM: Jak mam wyznaczyć współrzędne punktu E w zależności od a? Nie widzę tego.
16 kwi 18:34
Damian#UDM: Z tego, że ax+7−5a ∊ (2,10) ?
16 kwi 18:35
Saizou :
1) prosta k przechodząca przez D
2) E jako punkt przecięcia się prostej k oraz prostej AC
3) F jako punkt przecięcia się prostej k oraz prostej BC
16 kwi 18:37
chichi:
y
AC=x+1 ∧ y
BC=10
Punkt D∊y{EF} ∧ y=ax+b ⇒ 7=5a+b ⇒ b=7−5a ⇒ y=ax+7−5a
Nie potrafisz rozwiązywać układów równań?

16 kwi 18:37
Damian#UDM: No tak, mogę wyznaczyć równanie prostej AC. Dziękuje Saizou
16 kwi 18:40
Szkolniak:
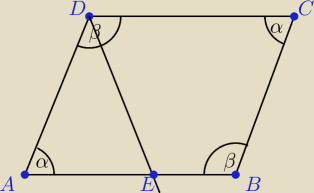
α=30
o,
|∡AED|=|∡ADE|=75
o, zatem ΔAED jest równoramienny ⇒ |AD|=|AE|=|BC|=4x, x>0
|AB|=|AE|+|EB|=4x+|EB|=(4+
√6−
√2)x, zatem:
|EB|=(4+
√6−
√2)x−4x
|EB|=(
√6−
√2)x
|DE|=y obliczamy z twierdzenia cosinusów w ΔDAE:
y
2=16x
2+16x
2−32x
2*cos30
o
y
2=32x
2−16
√3x
2
y
2=16x
2(2−
√3)
y=(4
√2−√3)x
Aby w czworokąt EBCD można było wpisać okrąg, musi zachodzić równość:
|EB|+|DC|=|DE|+|CB|
(
√6−
√2)x+(4+
√6−
√2)x=(4
√2−√3)x+4x /:x
√6−
√2+4+
√6−
√2=2(
√6−
√2)+4
2(
√6−
√2)+4=2(
√6−
√2)+4
L=P, zatem w czworokąt ten możemy wpisać okrąg, cnw.
16 kwi 19:17
Damian#UDM: 8. (0−3) KE 2020 PR
| | |AD| | | 2 | |
Na boku AB trójkąta ABC obrano punkt D w ten sposób, że |
| = |
| . Na odcinku CD |
| | |DB| | | 3 | |
obrano
| | |DF| | | 1 | |
taki punkt F , że |
| = |
| . Przez punkty B i F poprowadzono prostą, |
| | |DC| | | 4 | |
która przecięła bok AC w punkcie E. Uzasadnij, że stosunek pola trójkąta AEB do pola
trójkąta ECB jest równy 5:9.
19 kwi 01:00
Szkolniak: Właśnie sobie je próbuję i wpadłem na razie na to, że może pomocne będzie zaznaczenie przy
wierzchołku 'D' kątów α oraz 180o−α i zapisanie że pole całego trójkąta ABC będzie równe polu
ΔADC + pole ΔDBC z wykorzystaniem wzoru gdzie pojawia się sinus?
Może teraz spróbować policzyć pole trójkąta AEB lub ECB i potem odjąć od całości..
19 kwi 01:28
och&ach:
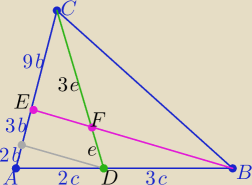
Wprowadzę bardziej przyjemne oznaczenia
| | 5b | |
P(ΔABE): P(ΔBCE)= |
| =5:9 |
| | 9b | |
19 kwi 01:46
Szkolniak: Twierdzenie Talesa?
19 kwi 01:47
och&ach:
tak

19 kwi 01:51
Szkolniak: Tylko 3 punkty za to że się to zauważy..

może dobrze że tylko, mało punktów by się straciło
na maturze
19 kwi 01:54
och&ach:

19 kwi 01:55
Damian#UDM: 10. (0−4) ZI 2021 PR VII
Wykres funkcji f(x)=x
3−6x
2+3x−7 przesunięto o wektor v i w wyniku tej operacji otrzymano
wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne
wektora v.
Z wygenerowanego wykresu odczytałem, że punkt, który po przesunięciu stanie się środkiem
symetrii to punkt S=(2,−17).
Zatem wykres został przesunięty o wektor v=[−2,17]
Pytanie jak to zadanie zrobić nie mając takich narzędzi

7. (0−3) ZI 2021 PR VII
Suma długości wszystkich wysokości trójkąta ABC jest 9 razy większa od promienia okręgu
wpisanego w ten trójkąt. Udowodnij, że trójkąt ABC jest równoboczny.
8. (0−3) ZI 2021 PR VII
Wykaż, że cos(40)cos(80)cos(160)=
−18
19 kwi 11:29
ICSP: 8)
Przemnóż licznik i mianownik przez 8sin(40) i następnie 3 razy zastosuj wzór na sinus
podwojonego kąta.
19 kwi 11:32
Damian#UDM: Dziękuję
ICSP tak zrobię

19 kwi 12:09
chichi:
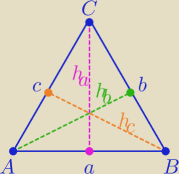
| | 1 | | 1 | | 1 | | 2P | | 2P | | 2P | |
PΔABC= |
| aha= |
| bhb= |
| chc ⇒ ha= |
| ∧ hb= |
| ∧ hc= |
| |
| | 2 | | 2 | | 2 | | a | | b | | c | |
| | 2P | | 2P | | 2P | | 18 | |
ha+hb+hc=9r ⇔ |
| + |
| + |
| = |
| / :2P, P>0 |
| | a | | b | | c | | a+b+c | |
Zostawiam Ci ostatnie przekształcenie i zauważenie równości pomiędzy średnimi

19 kwi 12:09
ichich:

19 kwi 12:17
chichi:
Chciałbym tylko zaznaczyć iż zadanie to pochodzi ze zbioru Pazdro dla klasy 1 LO, więc...

19 kwi 12:19
Damian#UDM: Dziękuję za informację.
19 kwi 12:31
Damian#UDM: | | sin(320) | |
ICSP po przekształceniach otrzymałem |
| |
| | 8sin(40) | |
19 kwi 13:12
Damian#UDM: I teraz sin(320)=sin(360−40), chyba dalej dam radę

19 kwi 13:12
chichi:
niech x=40
o, zatem mamy:
| | 1 | |
cos(x)cos(2x)cos(4x)=− |
| / *sin(x) |
| | 8 | |
| | 1 | |
sin(x)cos(x)cos(2x)cos(4x)=− |
| sin(x) |
| | 8 | |
| 1 | | 1 | |
| sin(2x)cos(2x)cos(4x)=− |
| sin(x) |
| 2 | | 8 | |
| 1 | | 1 | |
| sin(4x)cos(4x)=− |
| sin(x) |
| 4 | | 8 | |
sin(8x)=sin(x)
sin(320
o)=−sin(40
o)
Q.E.D. 
19 kwi 13:44
chichi:
sin(8x)=−sin(x) tam się minus zgubił

19 kwi 13:45
Szkolniak: I co z tego, że takie zadanie pochodzi ze zbioru zadań dla 1 klasy LO? Jak dla mnie trochę
niezbyt ten komentarz, zbędne takie 'docinki' − bo nie wiem jak inaczej to rozumieć.

19 kwi 14:15
chichi:
To z tego, że ktoś je stamtąd buchnął i wkleił do arkusza z zadania.info

19 kwi 14:18
chichi:
Aaaa, bo Ty to zinterpretowałeś jako docinkę, że jak jest z podręcznika dla 1 klasy, to jest
łatwe. Nie o to tam chodziło, tylko o to co napisałem wyżej

19 kwi 14:20
Szkolniak: Jak jest tak jak mówisz to przepraszam, ale właśnie tak to wyglądało w moich oczach

19 kwi 14:22
Saizou :
chichi ja bym się tak nie spinał odnośnie "kopiowania" zadań.
Praktycznie w każdym podręczniku znajdziesz zadanie typu:
udowodnij, że liczba postaci √3−2√2−√3+2√2 jest całkowita.
Dokładnie z takimi liczbami. Czy to plagiat?
Bardzo często się zdarza, że autorzy piszą zadania z pamięci i nie zawsze pamięta się skąd
jest dane zadanie.
19 kwi 14:27
chichi:
@
Saizou ja się nie spinam, tylko zaznaczyłem skąd pochodzi. Co do tego, że autorzy piszą
zadania z pamięci, to może być okej, natomiast przy tworzeniu arkuszy zadania powinno się
tworzyć nowe, nie szukać w pamięci zadań, które już zostały przez kogoś wymyślone

19 kwi 15:01
Saizou :
Może na jakieś ważne egzaminy, ale nie w wersji przygotowawczej

19 kwi 15:06
Damian#UDM: chichi to zadanie z sinusem zrobiłem sposobem
ICSP i też fajnie wyszło

19 kwi 20:50
Damian#UDM: A na zadanie 10. ktoś ma pomysł ?

19 kwi 20:51
ICSP: x3−6x2+3x−7 = x3 − 6x2 + 12x − 8 − 9x + 1 = (x−2)3 − 9(x−2) +17
v[−2 ,17]
19 kwi 21:06
Saizou :
10.
Wykres funkcji f(x)=x3−6x2+3x−7 przesunięto o wektor v i w wyniku tej operacji otrzymano
wykres, który jest symetryczny względem początku układu współrzędnych. Wyznacz współrzędne
wektora v.
Niech v =[p, q]. Wówczas po przesunięciu f o wektor v otrzymamy
g(x) = (x−p)3−6(x−p)2+3(x−p)−7+q.
g jest symetryczny względem układu współrzędnych, czyli zachodzi równość g(x) = −g(−x), tzn.
(x−p)3−6(x−p)2+3(x−p)−7+q = −[(−x−p)3−6(−x−p)2+3(−x−p)−7+q]
Przyrównaj wielomiany
19 kwi 21:09
chichi:
@
Damian#UDM to jest przecież to samo rozwiązanie, to nie wiem jak robiłeś sposobem
@
ICSP, ja po prostu mnożę przez 8 w ostatnim etapie, to jedyna różnica

19 kwi 21:18
ICSP: na końcu powinno być −17.
Wektor dobry.
19 kwi 21:26
Damian#UDM: chichi moje jest inne

Ja przekształcałem tylko lewą stronę, aż do szedłem do prawej, a
nie obie strony równania. Moim zdaniem to różnica

19 kwi 22:58
Damian#UDM: (0 − 2) PR JZMzM
Oblicz wartość wyrażenia |
√313−120√2−12
√2|
3 . Zakoduj cyfrę setek, dziesiątek i jedności
trzymanego wyniku.
Odpowiedź do 1|0|5
Nie mogę tego zwinąć. Wydaje mi się, że trzeba użyć wzoru skróconego mnożenia trzeciego
stopnia. Proszę o pomoc

23 kwi 12:16
Louie314: Zwinięcie obejdzie się za pomocą wzoru stopnia drugiego, będzie to (12√2−5)2 i chyba źle
przepisałeś odpowiedź, bo wyjdzie z tego |−5|3=125.
23 kwi 12:22
chichi:
|
√313−120√2−12
√2|
3=|
√(5−12√2)2−12
√2|
3=|12
√2−5−12
√2|
3=|−5|
3=125

23 kwi 12:23
ICSP: Przewidujesz:
√313 − 120√2 = a + b√2
a2 + 2b2 = 313
2ab = − 120
a2 + 2b2 = 313
ab = − 60
co po rozwiązaniu da np:
a = −5 , b = 12
23 kwi 12:24
figo:
313−120√2= (5−12√2)2
23 kwi 12:24
Damian#UDM: Tak, spojrzałem na inną odpowiedź. Dziękuję wam

23 kwi 12:31
Damian#UDM: To przewidywanie to super pomysł, wykorzystam go

23 kwi 12:31
6latek: √313−120√2= √313−√28800
√313−√28800= √x−√y i x≥y (przy roznicy )
podnosze do potegi drugiej obie strony
313−√28800= x+y−2√xy
x+y=313
−2√xy=−√28800
2{xy}=√28800
mam do rozwiazania uklad rownan
{x+y=313
{2√xy=√28800 − to rownanie do potegi drugiej
{x+y=313
{4xy=28800
x+y=313
xy=7200
po rozwiazaniu kilku przykladow te obliczenia dotad bedziesz robil w pamieci
x=313−y
(313−y)*y=7200
−y2+313y−7200=0
y2−313y+7200=0 −zmudne obliczenia
y=25 lub y=288
dla y=25 x=288
dla y=288x=25
stad dla x>y
√313−120√2= √288−√25= √144*2−5= 12√2−5
Dla prostych przykladow bedziesz takie pierwiastki liczyl w pamieci
Do obliczenia tego pierwiastka skorzystalbym z innego wzoru ale juz nie bede mieszal .
23 kwi 13:28
Damian#UDM:
19 kwi 2021 12:09
Chciałbym wrócić do rozwiązania chichi zadania z trójkątem, gdzie nie widzę tej zależności
między średnimi.
19 kwi 2021 21:09
Również chciałbym wrócić do rozwiązania zadania Saizou, zadanie z przesunięciem o wektor i
funkcją symetryczną,
Przyrównałem wielomiany i niestety nic mi nie wyszło.
Proszę o pomoc

Pozdrawiam
25 kwi 11:59
Louie314: 10.
f(x)=x3−6x2+3x−7
Ustalmy wektor v=[p,q].
Po przesunięciu:
g(x)=f(x−p)+q=(x−p)3−6(x−p)2+3(x−p)−7+q=−p3+3 p2x−6 p2−3px2+12px−3
p+q+x3−6x2+3x−7=x3+x2(−6−3p)+x(3p2+12p+3)−p3−6p2−3p+q−7
Ponadto wiadomo, że −g(−x)=g(x). Zatem:
−g(−x)=−(−x3+x2(−6−3p)−x(3p2+12p+3)−p3−6p2−3p+q−7)=x3−x2(−6−3p)+x(3p2
+12p+3)+p3+6p2+3p−q+7
−g(−x)=g(x)
x3−x2(−6−3p)+x(3p2+12p+3)+p3+6p2+3p−q+7=x3+x2(−6−3p)+x(3p2+12p+3)−p3−6p2−3p+q−7
−x2(−6−3p)+p3+6p2+3p−q+7=x2(−6−3p)−p3−6p2−3p+q−7
−2x2(−6−3p)+2p3+12p2+6p−2q+14=0
2x2(6+3p)+2p3+12p2+6p−2q+14=0
x2(6+3p)+p3+6p2+3p−q+7=0
To przekształcenie musi zachodzić dla każdego x należącego do dziedziny funkcji, zatem będziemy
chcieli pozbyć się x. Stąd:
6+3p=0
3p=−6
p=−2
q=17
Zatem ten wektor to v=[−2,17].
25 kwi 12:41
Damian#UDM: Dziękuje wam za pomoc

Na to z wektorem na pewno bym nie wpadł
Te matury z portalu zadania są dla mnie bardzo wymagające.
Podziwiam was, że potraficie zrobić większość zadań.
Miłego tygodnia wam życzę

26 kwi 18:14
Mila:
Damian, o to zadanie chodzi?
Suma długości wszystkich wysokości trójkąta ABC jest 9 razy większa od promienia okręgu
wpisanego w ten trójkąt. Udowodnij, że trójkąt ABC jest równoboczny.
26 kwi 18:49
Mila:
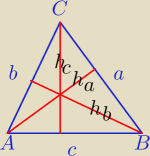
1) h
a+h
b+h
c=9r, gdzie r−promień okręgu wpisanego w ΔABC
P− pole ΔABC
2)
| | P | | a+b+c | |
P= p*r⇔r= |
| , gdzie p= |
| |
| | p | | 2 | |
| 2P | | 2P | | 2P | | 2*9P | |
| + |
| + |
| = |
| ⇔ |
| a | | b | | c | | a+b+c | |
| 1 | | 1 | | 1 | | 9 | |
| + |
| + |
| = |
| / *(a+b+c) |
| a | | b | | c | | a+b+c | |
| | b | | c | | a | | c | | a | | b | |
1+ |
| + |
| + |
| +1+ |
| + |
| + |
| +1=9⇔ |
| | a | | a | | b | | b | | c | | c | |
| | b | | a | | a | | c | | b | | c | |
(*) ( |
| + |
| )+( |
| + |
| )+( |
| + |
| )=6 |
| | a | | b | | c | | a | | c | | b | |
Wiemy , że dla dodatnich a, b, c Mamy:
| | b | | a | |
( |
| + |
| )≥2 i równość zachodzi dla a=b |
| | a | | b | |
| | a | | c | |
( |
| + |
| )≥2 i równość zachodzi dla a=c |
| | c | | a | |
| | b | | c | |
( |
| + |
| )≥2 i równość zachodzi dla b=c |
| | c | | b | |
równość (8) może zachodzić tylko w przypadku a=b=c⇔
Δ jest równoboczny.
Ze średnimi krócej, to zostawiam
Saizou i chichi
26 kwi 19:18
 Chciałbym wam życzyć miłego wieczoru i kolejnych dni
Chciałbym wam życzyć miłego wieczoru i kolejnych dni  A teraz zadania z matmy.
https://pdf.zadania.info/94253.pdf − rozwiązuje ten arkusz i mam problem z zadaniami: 6, 13 oraz 14.
W zadaniu 6. i 14. nie mam pomysłu.
W zadaniu. 13. nie wiem jak policzyć długości odcinków BF oraz BD, dzięki czemu mógłbym
skorzystać z twierdzenia cosinusów w trójkącie BFD.
Proszę o pomoc
A teraz zadania z matmy.
https://pdf.zadania.info/94253.pdf − rozwiązuje ten arkusz i mam problem z zadaniami: 6, 13 oraz 14.
W zadaniu 6. i 14. nie mam pomysłu.
W zadaniu. 13. nie wiem jak policzyć długości odcinków BF oraz BD, dzięki czemu mógłbym
skorzystać z twierdzenia cosinusów w trójkącie BFD.
Proszę o pomoc 





 https://matematykaszkolna.pl/forum/408997.html
https://matematykaszkolna.pl/forum/408997.html
 Np: tak
|KD|=2a−x , |AK|=3a+x , x∊(0,2a) x −−− z tw. o odcinkach stycznych
Np: tak
|KD|=2a−x , |AK|=3a+x , x∊(0,2a) x −−− z tw. o odcinkach stycznych

 Skorzystałem tylko z podobieństwa
trójkątów oraz tw. o odcinkach stycznych i doszedłem do takiej samej równości
Skorzystałem tylko z podobieństwa
trójkątów oraz tw. o odcinkach stycznych i doszedłem do takiej samej równości  zadanie za 4
punkty, a tyle liczenia.
Arkusze maturalne z zadania.info powinny być na 70 a nie 50 punktów
zadanie za 4
punkty, a tyle liczenia.
Arkusze maturalne z zadania.info powinny być na 70 a nie 50 punktów  wredulus świetny pomysł, nigdy bym na to nie wpadł
wredulus świetny pomysł, nigdy bym na to nie wpadł  Rozwiąże je w ten sposób sam.
6. zadanie robiłem podobnie z twierdzenia sinusów lecz nie znalazłem żadnego powiązania między
wartościami
Rozwiąże je w ten sposób sam.
6. zadanie robiłem podobnie z twierdzenia sinusów lecz nie znalazłem żadnego powiązania między
wartościami  No i zostało zadanie 13. zapraszam do pomagania
No i zostało zadanie 13. zapraszam do pomagania 
 Zawsze można na was liczyć.
Fajnie, że tutaj jesteście
Zawsze można na was liczyć.
Fajnie, że tutaj jesteście 
 Z treści zadania w ΔAMD |DM=24 i AM=10
ΔAMD ≡ ΔCNF to NF=24 i CN=10
z tw. cosinusów w ΔBAM wyznacz BM2
i z tw. Pitagorasa w ΔDMB m2
analogicznie z drugiej strony
w ΔBCN wyznacz BN2 (
i z Pitagorasa w ΔBNF n2
i już z górki
Z treści zadania w ΔAMD |DM=24 i AM=10
ΔAMD ≡ ΔCNF to NF=24 i CN=10
z tw. cosinusów w ΔBAM wyznacz BM2
i z tw. Pitagorasa w ΔDMB m2
analogicznie z drugiej strony
w ΔBCN wyznacz BN2 (
i z Pitagorasa w ΔBNF n2
i już z górki











 Tak, zapomniałem zmienić uprawnień.
https://drive.google.com/drive/folders/1aksH8EaMHyhJp8BzAMwfT45tTc2xBPGe?usp=sharing
Teraz powinno być ok.
Tak, zapomniałem zmienić uprawnień.
https://drive.google.com/drive/folders/1aksH8EaMHyhJp8BzAMwfT45tTc2xBPGe?usp=sharing
Teraz powinno być ok.
 Pozdrawiam was
Pozdrawiam was
 Należy wykazać,że e=2c
z treści zadania:
Należy wykazać,że e=2c
z treści zadania:

 Zad. 15 Zauważmy z rysunku, że pole czworokąta ABFE będzie największy, kiedy pole trójkąta EFB
będzie najmniejsze, dalej już łatwo
Zad. 15 Zauważmy z rysunku, że pole czworokąta ABFE będzie największy, kiedy pole trójkąta EFB
będzie najmniejsze, dalej już łatwo 





 AC =4√3
Z informacji o polu mamy, że
AC =4√3
Z informacji o polu mamy, że

 8. (0−3) PR
8. (0−3) PR
 Żeby nikt już nie popełniam więcej niepotrzebnych błędów
przez ukryte treści
Żeby nikt już nie popełniam więcej niepotrzebnych błędów
przez ukryte treści  .
.


 α=30o,
|∡AED|=|∡ADE|=75o, zatem ΔAED jest równoramienny ⇒ |AD|=|AE|=|BC|=4x, x>0
α=30o,
|∡AED|=|∡ADE|=75o, zatem ΔAED jest równoramienny ⇒ |AD|=|AE|=|BC|=4x, x>0
 Wprowadzę bardziej przyjemne oznaczenia
Wprowadzę bardziej przyjemne oznaczenia

 może dobrze że tylko, mało punktów by się straciło
na maturze
może dobrze że tylko, mało punktów by się straciło
na maturze

 7. (0−3) ZI 2021 PR VII
Suma długości wszystkich wysokości trójkąta ABC jest 9 razy większa od promienia okręgu
wpisanego w ten trójkąt. Udowodnij, że trójkąt ABC jest równoboczny.
8. (0−3) ZI 2021 PR VII
Wykaż, że cos(40)cos(80)cos(160)=−18
7. (0−3) ZI 2021 PR VII
Suma długości wszystkich wysokości trójkąta ABC jest 9 razy większa od promienia okręgu
wpisanego w ten trójkąt. Udowodnij, że trójkąt ABC jest równoboczny.
8. (0−3) ZI 2021 PR VII
Wykaż, że cos(40)cos(80)cos(160)=−18

















 Ja przekształcałem tylko lewą stronę, aż do szedłem do prawej, a
nie obie strony równania. Moim zdaniem to różnica
Ja przekształcałem tylko lewą stronę, aż do szedłem do prawej, a
nie obie strony równania. Moim zdaniem to różnica 




 Pozdrawiam
Pozdrawiam
 Na to z wektorem na pewno bym nie wpadł
Te matury z portalu zadania są dla mnie bardzo wymagające.
Podziwiam was, że potraficie zrobić większość zadań.
Miłego tygodnia wam życzę
Na to z wektorem na pewno bym nie wpadł
Te matury z portalu zadania są dla mnie bardzo wymagające.
Podziwiam was, że potraficie zrobić większość zadań.
Miłego tygodnia wam życzę 
 1) ha+hb+hc=9r, gdzie r−promień okręgu wpisanego w ΔABC
P− pole ΔABC
2)
1) ha+hb+hc=9r, gdzie r−promień okręgu wpisanego w ΔABC
P− pole ΔABC
2)