geometria analityczna silly goose: Mam dwa punkty należące do jednego okręgu B(−2,6) i A(5,5), jak naleźć xc punktu C(xc, −3), który również należy do tego okręgu?

janek191: ( x + 2)² + ( y − 6)² = r² ( x − 5)² + ( y − 5)² = r² ( x − x_c)² + ( x + 3)² = r²

janek191: III równanie (x − x_c)² + ( y + 3)² = r²

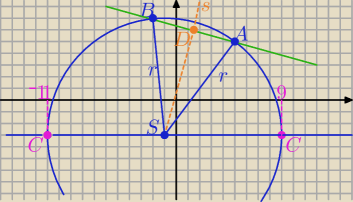
och&ach: 1/ środek S(x,y) leży na symetralnej odcinka AB napisz równanie tej symetralnej ...... s: y=7x−10 to S(x, 7x−10) 2/wyznacz S z równości : |AS|²=|BS|² ...... S(−1.−3) i |AS|²=r² ⇒ r=10 to |SC|²=r² ...... (x_C+1)²= 100 ....... x_c= 9 lub x_c= −11

silly goose: |AS|²=|BS|² co to za równość?

och&ach: |AS|²=|BS|²= r²

chichi: Taki czytelny rysunek, a Ty jeszcze pytasz skąd ta równość ehh..

och&ach:

chichi:

och&ach:

silly goose: nie wiem jak wyznaczyć S nie widze tego

chichi: @Eta źle wyznaczyła równanie prostej na której znajduje się środek okręgu, więc poprawię:

	1		3		11		11		21
aAB=−		⇒ aOS=7 ∧ S=(		,		) ⇒		=		+b ⇒ b=−5 ⇒ yOS=7x−5
	7		2		2		2		2

chichi: Tych okręgów jest nieskończenie wiele, nie da się jednoznacznie wyznaczyć x_c

Mila: https://matematykaszkolna.pl/forum/409065.html

chichi: @Mila teraz widzę, że to jest to zadanie, ale autor postu nie podał danych, które jednoznacznie pozwalają wyznaczyć ten okrąg, stąd mój wpis z 17:20 jest prawdziwy

Mila: Zauważyłam Ja domyśliłam się, bo wczoraj było podobne pytanie.

chichi: No ja rozwiązywałem tamto zadanie, ale tyle się tych zadań robi, że trudno je wszystkie spamiętać, dopiero Twój link mi przypomniał

Mila: Właśnie kilka osób rozwiązywało to zadanie więc ja zrezygnowałam z niego, ale wczoraj było pytanie dotyczące tego zadania, to rozwiązałam i dałam wskazówki, co wystarczyło.

chichi: Tak to jest jak się wkleja wybrakowane polecenia...

silly goose: przepraszam, myślałam, że tylko to jest mi potrzebne..... : / ale dalej nie wiem jak to policzyć

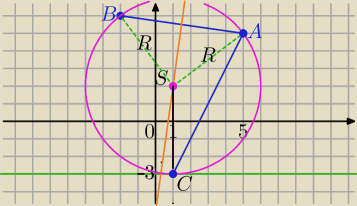
Mila: A=(5,5), B=−2,6) to obliczyłaś? 1) okrąg opisany na ΔABC jest styczny do prostej y=−3 w punkcie C. Promień jest prostopadły do y=−3 w punkcie styczności. S=(x,y) − środek okręgu opisanego na ΔABC i S leży na symetralnej odcinaka AB Symetralna AB− zbiór punktów jednakowo odległych od punktów A i B⇔ (x−5)²+(y−5)²=(x+2)²+(y−6)²⇔ y=7x+5 Punkt C=(c,−3) pierwsza wsp. punktu S też jest równa c. S=(c,7c−5), A=(5,5) |AS|=|CS| (c−5)²+(7c−5−5)²=(c−c)²+(7c−5+3)² c=1 lub c=121 C=(1,−3) lub C=(121, −3)

silly goose: tak punkty A, B obliczyłam sama, dziękuje bardzo za wytłumaczenie