relacja zwrotna
gorgonek: Cześć. Mam pewien problem z liczebnością relacji zwrotnych i przechodnich (zbiór pusty).
1) Czy możliwy jest fakt, że liczba relacji zwrotnych wynosi 0,5 − dla badanego zbioru pustego?
Według twierdzeń matematycznych, relacja pusta nie może być zwrotna, zatem jak można
rozpatrywać wynik 0,5, ze wzoru:
Ilość relacji zwrotnych: 2 do potęgi (n2 − n)
2) Próbuję się doszukać, jak wyznaczyć liczebność przechodniości na zadanym zbiorze. Wiem, że
relacja przechodnia to również zbiór pusty, jednak czy orientuje się ktoś odnośnie wzoru na
wyznaczenie jej liczebności? Czy da się skorzystać tutaj w jakiś sposób z liczby permutacji z
powtórzeniami i jednocześnie wykluczeniem pewnych powtórzeń?
Byłbym zobowiązany za wszelką pomoc!
Pozdrawiam serdecznie.
1 maj 11:33
ds: 1=2 łatwe
1 maj 11:36
Legend of whitesnake : Jak łatwo jest odpisać drugiemu łatwe nie wyjaśniajac dlaczego to jest łatwe
Byc może pierwsza lepsza wskazówka byłaby strzałem w dziesiątkę
1 maj 11:47
ite:
1/ skąd dla zbioru pustego masz wynik 0,5 ?
czy we wzorze 2
n2−n nie ma zastrzeżenia, że n∊ℕ
+ ?
1 maj 13:11
ite: I czy chodzi Ci o relację pustą określaną na zbiorze pustym?
1 maj 13:15
gorgonek: Udało się rozwiązać pierwszy problem

Także, dzięki wielkie Ite za wskazówkę, po prostu raz
podstawiłem wzór pod n = 1, a innym razem za n = 0, co powodowało wynik połówkowy.
Natomiast, ciekawym jest fakt, że na ilość relacji przeciwzwrotnych jest dokładnie ten sam
wzór, a więc także wynikiem w relacji przeciwzwrotnej będzie 1. Zatem, czy wtedy nie powinno
się uznać takiej wartości? (jeśli zwrotność wyklucza przeciwzwrotność)?
1 maj 15:45
ite:
Jeśli wyobrazimy sobie iloczyn kartezjański zbioru, z którego elementów tworzymy relację w
postaci takiej jak tu:
https://matematykaszkolna.pl/forum/396953.html
to łatwo zauważyć, że relacja jest zwrotna, gdy należą do niej wszystkie pary leżące na
przekątnej, a przeciwzwrotna − gdy nie należy żadna z tych par.
Te sytuacje oczywiście wykluczają, więc zwrotność wyklucza przeciwzwrotność, chociaż nie są to
jedyne możliwości. Istnieją relacje, które nie są ani takie, ani takie.
Ilość wszystkich relacji i zwrotnych, i przeciwzwrotnych zależy jedynie od ilości pozostałych
par w relacji = tych poza przekątną. I od tego które z nich do relacji należą.
Tych par jest dla zbioru n−elementowego (n
2−n). Stąd to 2
n2−n.
I dlatego sposób liczenia ilości obu relacji jest ten sam.
1 maj 17:27
gorgonek: Zgadza się. Patrząc na owy diagram Hassego można dostrzec jednakową liczbę relacji zwrotnych i
przeciwzwrotnych.
Jeśli mogę jeszcze spytać, czy do narysowania Diagramu Venna, wystarczą następujące relacje?:
− liczba relacji zwrotnych,
− liczba relacji symetrycznych,
− liczba relacji zwrotnych i symetrycznych
Posiadam jeszcze liczbę relacji antysymetrycznych i przeciwsymetrycznych, jednak aby powstał
schemat trójkołowy, wypadałoby również dodać liczbę relacji przechodnich, a także zwrotnych i
przechodnich oraz symetrycznych i przechodnich, a także relację równoważności. Zatem, czy te
pierwsze trzy relacje powinny wystarczyć do wykazania zależności z dwóch okręgów diagramu
Venna?
4 maj 13:30
ite:
1 maj 17:27 to jest odesłanie do zapisu relacji za pomocą tabeli, jest to coś innego niż
diagram Hassego.
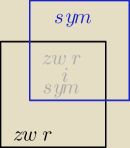
Czy na diagramie Venna ma być narysowane coś takiego jak wyżej? Nie za bardzo rozumiem to
pytanie.
5 maj 10:42
 Także, dzięki wielkie Ite za wskazówkę, po prostu raz
podstawiłem wzór pod n = 1, a innym razem za n = 0, co powodowało wynik połówkowy.
Natomiast, ciekawym jest fakt, że na ilość relacji przeciwzwrotnych jest dokładnie ten sam
wzór, a więc także wynikiem w relacji przeciwzwrotnej będzie 1. Zatem, czy wtedy nie powinno
się uznać takiej wartości? (jeśli zwrotność wyklucza przeciwzwrotność)?
Także, dzięki wielkie Ite za wskazówkę, po prostu raz
podstawiłem wzór pod n = 1, a innym razem za n = 0, co powodowało wynik połówkowy.
Natomiast, ciekawym jest fakt, że na ilość relacji przeciwzwrotnych jest dokładnie ten sam
wzór, a więc także wynikiem w relacji przeciwzwrotnej będzie 1. Zatem, czy wtedy nie powinno
się uznać takiej wartości? (jeśli zwrotność wyklucza przeciwzwrotność)?
 1 maj 17:27 to jest odesłanie do zapisu relacji za pomocą tabeli, jest to coś innego niż
diagram Hassego.
Czy na diagramie Venna ma być narysowane coś takiego jak wyżej? Nie za bardzo rozumiem to
pytanie.
1 maj 17:27 to jest odesłanie do zapisu relacji za pomocą tabeli, jest to coś innego niż
diagram Hassego.
Czy na diagramie Venna ma być narysowane coś takiego jak wyżej? Nie za bardzo rozumiem to
pytanie.