Relacja porządku - Matematyka Dyskretna
NieUmiem: W zbiorze N określono relację porządku wzorem: xRy <=> (x−1) | (y−1).
Wyznaczyć elementy wyróżnione i kresy zbioru A = {2,4,5,7,10,13}
Mógłby ktoś rozpisać mi łopatologicznie krok po kroku jak się rozwiązuje takie zadanie?
9 lut 06:42
Adamm:
Czy element wyróżniony = maksimum lub minimum?
9 lut 10:04
NieUmiem: Tak
9 lut 17:03
Maciess: Rysuj diagram Hassego
9 lut 21:44
Maciess: zauważ że ∀y∊A 2Ry
9 lut 21:47
Maciess:
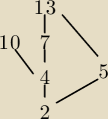
Wg mnie to tak i stąd juz wszystko widać.
9 lut 21:59
ite:
A ja polecam zacząć od takiej tabeli (i dopiero na jej podstawie diagram Hassego), łatwiej
będzie.
9 lut 22:00
Maciess: inf A = 2
sup A = 37 (?)
2 jest elementem najmniejszym w A . 10 i 13 to elementy maksymalne w A.
9 lut 22:04
NieUmiem: W dalszym ciągu mało rozumiem, szczególnie:
dlaczego kres górny wynosi 37,
dlaczego są dwa elementy maksymalne.
9 lut 22:19
Maciess: Czy znasz definicję?
9 lut 22:59
NieUmiem: Dobra, już wiem jak się wyznacza te elementy minimalne i maksymalne z diagramu Hassego,
ale nie wiem skąd wziąć te kresy.
Kres górny (supremum) − najmniejsze możliwe ograniczenie z góry
Kres dolny (infimium) − największe możliwe ograniczenie z góry
Dla danego zbioru A mamy: sup A = 13, inf A = 2
Dla liczb naturalnych: sup = nie istnieje (nieskończoność), inf= 1
I jak mam to powiązać ze sobą? Dlaczego sup A to u Ciebie 37, a nie właśnie 13?
9 lut 23:23
ite: sup A = 25 (?)
9 lut 23:23
NieUmiem: Oczywiście wkradł się błąd:
Kres dolny (infimium) − największe możliwe ograniczenie z DOŁU
9 lut 23:26
Pytający:
NieUmiem, sup(A) ≠ 13, bo przykładowo (10, 13)∉R (przecież 9 nie jest dzielnikiem 12).
Ite, podobnie sup(A) ≠ 25, bo przykładowo (10, 25)∉R (przecież 9 nie jest dzielnikiem 24).
Generalnie najmniejszym ograniczeniem górnym A będzie najmniejsza taka liczba (naturalna),
która pomniejszona o 1 będzie podzielna przez każdy element A pomniejszony o 1. Inaczej:
sup(A) − 1 = NWW(2 − 1, 4 − 1, 5 − 1, 7 − 1, 10 − 1, 13 − 1)
⇒
sup(A) = NWW(1, 3, 4, 6, 9, 12) + 1 = 36 + 1 = 37.
9 lut 23:47
ite: Dzięki za wyjaśnienie.
Dodatkowe pytanie: gdyby dodać jeszcze taki warunek xRy ⇔ (x−1) | (y−1) ∧ x≠y, to już nie
byłaby relacja porządku i wyznaczanie elementów wyróżnionych nie byłoby możliwe?
10 lut 19:16
10 lut 19:27
ite: Dziekuję!
10 lut 19:35
