maturka dzonypieczony:

	1
Dana jest funkcja f(x)=2x2+(m−4)x−2m+
	2

. Wyznacz wszystkie wartości parametru m , dla których funkcja f ma dwa różne miejsca zerowe, z których każde jest większe niż 3. wyliczam dziedzinę z zalozenia deltwa wieksza niz 0 i potem z drugiego warunku ze kazde z dwoch miejsc

	−b−√Δ
zerowych jest wieksze od 3 pisze ze		>3 i analogicznie wzor na x2 i wychodzi mi z
	2a

pierwszego zalozenia z x₁: m−√m²+8m+12>8 i nie wiem jak to dalej rozwiazac bo nie moge podniesc do kwadratu obydwoch stron zeby sie pierwiastka pozbyc z racji że nie wiem co to są za liczby pod parametrem wiec prosze o pomoc

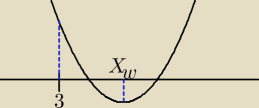
Philips: hmm, a może inne warunki? każde z miejsc zerowych jest większe niż 3, robimy tak: f(3)>0 x_w>3

Philips:

6latek: To ze Δ>0 to nie wyznaczasz dziedziny funkcji tylko wyznaczasz dla jakiego m funkcja ta ma dwa rozne miejsca zerowe Naturalna dziedzina tej funkcji jest zbior liczb ℛ gdyz to jest wielomian .

ICSP: https://matematykaszkolna.pl/forum/408841.html Masz tam trzy sposoby na rozwiązanie tego zadania

dzonypieczony: Dzieki wielie philips, a co do ICSP to nie rozumiem tam jednego, czemu tam przy Twoim sposobie jest założenie |m|>6 w sensie na co nam pozwala to założenie bo nie bardzo rozumiem i nie wiem jakie miałbym ttutaj dać założenie z m

dzonypieczony: 6latek Δ>0 to u mnie dziedzina funkcji f(m)

ICSP: |m| > 6 ponieważ pierwiastki muszą istnieć ( Δ > 0)

dzonypieczony: racja

dzonypieczony: @ICSP

dzonypieczony: jak kogos oznaczyc xd

dzonypieczony: jest problem bo z tymi zalozeniami nie moze mi wyjsc poprawny wynik i juz sam nw co jest zle po wszystkich obliczeniach mam z trech założeń 1)Δ>0, 2)f(3)>0, 3)X_w>3 1)= m∊(−∞;−2)u(−6;∞)

	1
2)= m∊(−6		;∞)
	2

3)= m∊(−∞;−8)

	1
a powinno wyjsc ze sumy tego przedzial m∊(6		;8)
	2

nie mam zielonego pojęcia gdzie mogłem błąd zrobić, jak ktoś byłby w stanie to roziwązać to byłbym bardzo wdzięczny

ICSP: Widać coś jest nie tak z treścią.

6latek: Ja takze sprawdzalem obliczenia OK tylko 1 przedzial tak m∊(−∞.−6)U(−2,∞) Albo nie ta odpowiedz do zadania

Mila: Sprawdź czy dobrze napisałeś treść zadania i czy dobrze zobaczyłeś odpowiedź.

6latek: Dobry wieczór

Philips: a to matura za 2 tygodnie heh

Mila: Dobry wieczór, jak widzimy autor nie reaguje na nasze pytania. Podejrzewam błąd w zapisie.