najdź te wartości parametru m, dla których funkcja f(x)=x^2+mx+9 ma dwa miejsca
Ktos2:
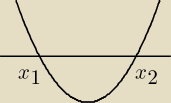
znajdź te wartości parametru m, dla których funkcja f(x)=x
2+mx+9 ma dwa miejsca zerowe większe
od 2.
założenia Δ>0
rysuję wykres liczę deltę i wychodzi mi Δ=m
2−36
x
1 > 2 ⋀ x
2 > 2
pozbywam się ułamka mnożąc przez 2
−m−
√Δ > 4 ⋀ −m+
√Δ > 4
−m−
√m2−36 > 4 ⋀ −m+
√m2−36 > 4
podnoszę do kwadratu stronami korzystając ze wzoru skróconego mnożenia
(−m−
√m2−36)
2 > 16 ⋀ (−m+
√m2−36)
2 > 16
m
2−2m*
√m2−36+m
2−36 > 16 ⋀ m
2−2m*
√m2−36+m
2−36 > 16
2m
2−2m*
√m2−36 > 52 ⋀ 2m
2−2m*
√m2−36 > 52
co dalej?
5 kwi 20:16
Filip:
zalozenia Δ > 0 wiec rozwiazujesz tylko nierowno m2−36>0
5 kwi 20:21
Filip: a nie doczytalem ze dwa miejsca zerowe WIEKSZE od 2
5 kwi 20:22
Filip:
f(x)=x2+mx+9
Warunki zadania
Δ>0
f(2)>0
xw>2
5 kwi 20:23
Ktos2: skąd f(2)>0 i xw>2?
5 kwi 20:35
Filip: wystarczy sobie spojrzec na rysunek, gdy parabola ma dokladnie dwa miejsca zerowe i a>0,
warunek f(2)>0 mowi nam o tym, ze ta nasza funkcja bedzie miec miejsca zerowe (oba) albo
mniejsze od 2, albo wieksze od 2, jezeli chcemy, by miala wieksze od 2, musimy dodac warunek,
iz wierzcholek paraboli a raczej xw bedzie wieksze od 2, czyli mamy xw>2
5 kwi 22:22
Ktos2: xw>2 jeszcze rozumiem ale f(2)>0 nie bardzo
6 kwi 10:34
Filip:
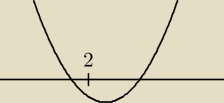
zauwaz, ze gdyby nie bylo tego f(2)>0 to mozesz miec taka parabole jak na rysunku, czyli jak
widac jedno miejsce zerowe jest mniejsze od 2
6 kwi 10:37
Filip:
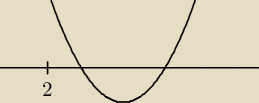
a teraz, f(2)>0 to mozemy miec taka sytuacje, lub ta parabola bedzie lezec na lewo, czyli
bedzie miec albo dwa miejsca zerowe wieksze od 2, albo dwa mniejsze, plus x
w>0 daje nam
warunek, ze beda to dwa wieksze
6 kwi 10:38
Ktos2: proszę jeszcze o rozrysowanie mi przypadku gdy jest f(2)>0 ale bez warunku xw>0
6 kwi 10:42
Ktos2: "albo dwa mniejsze"
tego też nie bardzo rozumiem
6 kwi 10:43
Filip:
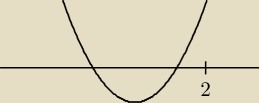
a tak? Mamy dwa przypadki, u ciebie w funkcji a>0 wiec rozwazamy parabole skierowana ramiona do
gory, tutaj i w 10:38 pokazalem, gdy f(2)>0, moga byc dwie mozliwosci, dlatego dokladamy
jeszcze ten warunek x
w>2
6 kwi 10:55
Ktos2: dzięki bardzo

6 kwi 11:00
szymkox777: Czy ostatecznie m ∊ (−6,5 ; −4) ?
6 kwi 12:20
Filip: nie wiem jaki jest wynik finalny, bo nie policzylem, po wypisaniu warunkow zostala yylko czesc
matematyczna i zmudne obliczenia
6 kwi 12:25
Mila:
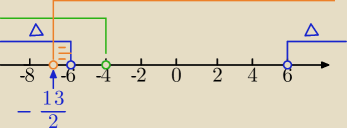
f(x)=x
2+mx+9
1) Δ=m
2−36
m
2−36>0
m<−6 lub m>6
2)
i
m<−4
i
odp.
6 kwi 20:31
ICSP: Można też pociągnąć oryginalne rozwiązanie.
Mamy:
chcemy, aby x
1 > 2 i x
2 > 2
Z tym, że x
2 > x
1, więc wystarczy aby x
1 > 2 przy warunku |m| > 6
−m −
√m2 − 36 > 4
m +
√m2 − 36 < −4
√m2 − 36 < −4 − m
musi być −4 − m > 0 ⇒ m < −4
Teraz podnosząc stronami do kwadratu
m
2 − 36 < m
2 + 8m + 16
8m + 52 > 0
czyli ostatecznie:
6 kwi 20:47
ICSP: Kolejny sposób:
Po pierwsze musi być: Δ > 0 ⇒ |m| > 6
x
1 > 2 ∧ x
2 > 2
x
1 − 2 > 0 ∧ x
2 − 2 > 0
(x
1 − 2)(x
2 − 2) > 0 ∧ x
1 − 2 + x
2 − 2 > 0
x
1x
2 − 2(x
1 + x
2) + 4 > 0 ∧ x
1 + x
2 > 4
9 + 2m +4 > 0 ∧ −m > 4
| | −13 | |
m > |
| ∧ m < −4 ∧ |m| > 6 |
| | 2 | |
Jak widać warunki prędzej czy później wyjdą takie same.
6 kwi 20:51
Filip: tak jak mowilem, zmudne obliczenia
6 kwi 21:21
 znajdź te wartości parametru m, dla których funkcja f(x)=x2+mx+9 ma dwa miejsca zerowe większe
od 2.
założenia Δ>0
rysuję wykres liczę deltę i wychodzi mi Δ=m2−36
x1 > 2 ⋀ x2 > 2
znajdź te wartości parametru m, dla których funkcja f(x)=x2+mx+9 ma dwa miejsca zerowe większe
od 2.
założenia Δ>0
rysuję wykres liczę deltę i wychodzi mi Δ=m2−36
x1 > 2 ⋀ x2 > 2
 zauwaz, ze gdyby nie bylo tego f(2)>0 to mozesz miec taka parabole jak na rysunku, czyli jak
widac jedno miejsce zerowe jest mniejsze od 2
zauwaz, ze gdyby nie bylo tego f(2)>0 to mozesz miec taka parabole jak na rysunku, czyli jak
widac jedno miejsce zerowe jest mniejsze od 2
 a teraz, f(2)>0 to mozemy miec taka sytuacje, lub ta parabola bedzie lezec na lewo, czyli
bedzie miec albo dwa miejsca zerowe wieksze od 2, albo dwa mniejsze, plus xw>0 daje nam
warunek, ze beda to dwa wieksze
a teraz, f(2)>0 to mozemy miec taka sytuacje, lub ta parabola bedzie lezec na lewo, czyli
bedzie miec albo dwa miejsca zerowe wieksze od 2, albo dwa mniejsze, plus xw>0 daje nam
warunek, ze beda to dwa wieksze
 a tak? Mamy dwa przypadki, u ciebie w funkcji a>0 wiec rozwazamy parabole skierowana ramiona do
gory, tutaj i w 10:38 pokazalem, gdy f(2)>0, moga byc dwie mozliwosci, dlatego dokladamy
jeszcze ten warunek xw>2
a tak? Mamy dwa przypadki, u ciebie w funkcji a>0 wiec rozwazamy parabole skierowana ramiona do
gory, tutaj i w 10:38 pokazalem, gdy f(2)>0, moga byc dwie mozliwosci, dlatego dokladamy
jeszcze ten warunek xw>2

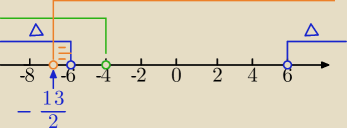 f(x)=x2+mx+9
1) Δ=m2−36
m2−36>0
m<−6 lub m>6
2)
i
f(x)=x2+mx+9
1) Δ=m2−36
m2−36>0
m<−6 lub m>6
2)
i