Okrąg, proste styczne. PR7: Mam pewien problem odnośnie tego zadania, proszę o przeczytanie do końca i konieczne jest wejście w ten link niżej z tego samego forum bo tam jest rysunek. Znam już kilka osób ogarniętych w tym temacie, @Mila i @ICSP jakbyście mogli pomóc byłbym wdzięczny. Znajdź równanie okręgu stycznego do prostej k: x+y+13=0 i do prostej m: 7x− y−5=0 w punkcie A(1,2) − wiem że można to rozwiązać na 3 sposoby jak tutaj https://matematykaszkolna.pl/forum/408762.html ( są one opisane w 4 ostatnich wiadomościach), ale postanowiłem to zrobić pisząc równanie okręgu wykorzystując proste styczne trochę inaczej: "1" Można ułożyć OD RAZU równanie okręgu dla S( a , −3a−15) leżącego na dwusiecznej 3x+y+15=0 i stycznego do jednej z tych prostych (tutaj promień może być równy tylko i wyłącznie odległości środka od punktu (1,2), bo jeśli się napisze że r = odległości środka od jednej z prostej do której jest styczny to wyjdzie b ∊ R, dlatego że stąd wyznaczaliśmy to równanie dwusiecznej ) (x−a)²+(y−b)²=r² , gdzie y to jest jedna z prostych stycznych (x−a)² + (−x−13−(−3a−15)² = (a−1)²+(−3a−15−2)² stąd 2x²+(−8a−4)x−88a−286 = 0, czyli okrąg ma jeden punkt wspólny ( jest styczny ) gdy Δ = 0, zatem gdy a = −6 ( no i tak samo trzeba by było zrobić dla drugiej dwusiecznej bo są dwa takie okręgi i potem jeszcze obliczyć b i promień...) "2" ALE można też tym sposobem zrobić biorąc pod uwagę tylko prostą prostopadłą "n" do prostej m w punkcie (1,2) o równaniu x+7y−15=0 i wtedy Można ułożyć równanie okręgu dla S(−7b+15, b) leżącego na tej prostej "n" i stycznego do jednej z prostych stycznych (m lub k) (x−a)²+(y−b)²=r² , gdzie y to jest jedna z prostych stycznych ALE mam tutaj problem − można tutaj zrobić kombinacje " podstawiając za y ( prostą m lub k ) i za promień odległość środka od jednej prostej stycznej / drugiej prostej stycznej lub odległość od punktu A(1,2), tylko że podobnie jak w "1" dla niektórych kombinacji wyjdzie b ∊ R , ale najpierw kiedy tak nie będzie tzn otrzymamy dokładnie b : 1) biorąc za y pierwszą styczną "m" ( tą z punktem A ) i za promień odległość środka od drugiej stycznej "k" (x−(−7b+15))² + (−3x−15−b)² = (−7b+15−1)²+(b−2)² , po wyliczeniu delty i przyrównaniu do 0 otrzymamy dokładnie b1 i b2. 2) biorąc na odwrót tzn za y drugą styczną "k" a za promień odległość środka od pierwszej stycznej tzn prostej "m" również otrzymamy dokładnie b1 i b2 3) biorąc za y drugą styczną "k" oraz za promień odległość środka od punktu A również otrzymamy dokładnie b1 i b2 natomiast dla takich kombinacji: 4) biorąc za y drugą styczną "k" i za promień odległość środka od tej stycznej otrzymamy b ∊ R ( bo po prostu wzięliśmy jedną i tą samą prostą ) i tutaj mam pytanie do 5) i 6): 5) biorąc za y pierwszą styczną "m" i za promień do ² odległość środka od tej stycznej to nie otrzymamy wgl "b" tzn nie będzie tak jakby należał wgl ∊ R? Bo po podniesieniu do kwadratu (x−(−7b+15))²+(7x−5−b)² = ^{(7(−7b+15)−b−5)2}₅₀ wyjdzie delta pozbawiona "b", bo "b" się skróciło tzn wyjdzie delta z samym "x" : 50x²−100x+50, więc nie mamy info o "b" i tak samo w 6) biorąc za y też pierwszą styczną ale za promień odległość środka od A do ()², też otrzymamy taką samą deltę, i tutaj mam pytanie, czy to również oznacza że po prostu b ∊ R? Czy? Myślałem że po prostu dla 4), 5) i 6) wyjdzie w każdym przypadku b ∊ R ale teraz się zdziwiłem, bo dla 1), 2) i 3) jest to oczywiste, dlaczego otrzymujemy dokładnie b₁ i b₂, bo po prostu stąd nie wyznaczaliśmy/ się nie wyznacza równania tej prostej "n" więc można tak zrobić

PR7: Chodzi mi po prostu o to, że jak normalnie wyznacza się prostą prostopadłą do prostej "m" w punkcie A to potem układa się równanie Albo odległość środka od jednej prostej ( k ) = odległości środka od prostej (m) i tutaj za x i y, dawaliśmy współrzędne środków tzn S(−7b+15, b) Albo odległość drugiej prostej (k) od środka = odległości środka od punktu A Bo inaczej robiąc wyszło by że b ∊ R, tylko że tutaj w punktach 5) i 6) robiąc tak nie otrzymuje wgl "b" po podniesieniu do kwadratu i zostaje samo równanie z "x" tj. 50x²−−100x+50 gdzie stąd delta wyjdzie = 0, tzn 100²−4*50*50 = 0, więc to oznacza też że b ∊ R? Tak samo jak w punkcie 4)? Bo w 4) tam znów otrzymałem b ∊ R ale po podniesieniu do kwadratu tych czynników w równaniu miałem coś związanego z b, na przykład 50x²−(20b+10)x+100−10b² ( coś tego typu ), więc po wyliczeniu delty i przyrównaniu do zera wychodziło 0 = 0 więc wiadomo że b należy ∊ R, natomiast w 5) i 6) też to oznacza ? Że b ∊ R ? Mimo że wychodzi równanie wgl bez "b"?

PR7: I też mam pytanie dlaczego akurat dla tych dwóch kombinacji wychodzi właśnie równanie po podniesieniu tych czynników do kwadratu pozbawione "b"? A dla innych jest coś związanego z b Tylko po prostu potem z delty wynika że b € R? Równanie o którym mówię to (x−(−7b+15))²+(7x−5−b)² = ^{(7(−7b+15)−b−5)²}₅₀

PR7: Ad. 1) Poprawka 1) biorąc za y pierwszą styczną "m" ( tą z punktem A ) i za promień odległość środka od drugiej stycznej "k", gdzie okrąg leży na prostej prostopadłej "n" x = −7y+15 ,. S(−7b+15, b ) a za y bierzemy równanie prostej "m" y = 7x−5 a za promień odległość środka od prostej "k" o równaniu: x+y+13=0

	((−7b+15)+b+13)²
(x−(−7b+15))² + (7x−5−b)² =
	2

Po wyliczeniu delty i przyrównaniu do 0 otrzymamy dokładnie b1 i b2. −−−−−−−−−−−−−− Natomiast 3) biorąc za y drugą styczną "k" ( bez punktu A, bo gdyby wziąć jak w punkcie 6) prostą styczną "m" czyli zamiast y= −x−13 dać y = 7x−5 to wyjdzie 0 = 0 ) oraz za promień odległość środka od punktu A, również otrzymamy dokładnie b1 i b2 Wtedy do 3) (x−(−7b+15))² + (−x−13−b)²= (−7b+15−1)²+(b−2)²

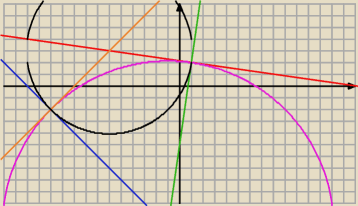piotr: kolejność obliczeń: 1)prosta czerwona: y=(−x+15)/7 2) okrąg fioletowy: (x+1)²+(y+12)²=200 3)prosta pomarańczowa: y=x+9 4)szukany okrąg: (x+6)²+(y−2)²=50