Okrąg, styczna i punkt ABcd: Mam pytanie czy jeśli mamy np prostą y= 2x+1 ( dowolną ) oraz punkt który nie leży na niej, to czy dobrze myślę, że może być nieskończenie wiele okręgów, Które jednocześnie przechodzą przez ten punkt oraz są styczne do tej prostej ? Sam próbowałem to sprawdzić, najpierw poprowadziłem prostą równoległą do y= 2x+1 która przechodzi przez ten punkt np (−3,6) i potem znalazłem pomiędzy tymi dwoma prostymi prostą ( równoległą i równoodległą ) na której leży jeden okrąg ( pierwszy przypadek ) no i tutaj otrzymałem jeden okrąg Próbowałem też poprowadzić prostą prostopadłą ( nazwijmy ją y2) do y = 2x+1 oraz przechodząca przez punkt (−3,6) i wtedy wyszły mi kolejne dwa okręgi I teraz gdybym to jeszcze sprawdził dla dwusiecznych tych dwóch prostych ( y = 2x+1 oraz y2 ) To pewnie dalej by mi wyszły po dwa okręgi dla każdej dwusiecznej ( są dwie ) Ale to nie wszystko prawda ? Bo tutaj może prowadzić dowolne proste prostopadłe, albo po prostu Przechodzące przez punkt (−3,6) i przecinające prostą y = 2x+1 i takich okręgów wtedy Wyjdzie więcej, tak?

ite: Dobrze myślisz : ) Tutaj jest podany punkt i prosta. https://www.geogebra.org/geometry/bnq7qttu Takich okręgów jest nieskończenie wiele. Jaką krzywą tworzy zbiór ich środków?

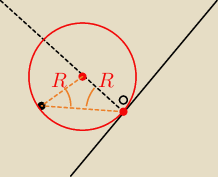
ite: Podany opis konstrukcji z prostymi prostopadłymi i dwusiecznymi nie jest dla mnie jasny, więc proponuję taki, oparty na prostych prostopadłych i trójkątach równoramiennych.

ABcd: Parabolę − muszę się jeszcze nauczyć robić takie wykresy z animacją. Dzięki wielkie za odpowiedź

P81: @ite Mam pytanie, ten wzór paraboli załatwiła za Ciebie ta strona czy sam musiałeś go znaleźć? Jeśli tak To podałbyś obliczenia? Bo tam jest napisane Np. Parabola(P,f) i wydaje mi się, że trudno jest samemu Znaleźć równanie tej paraboli i raczej to program na stronie geogebra zrobił to.

ICSP:

	|2x − y + 1|
√(x+3)2 + (y − 6)2 =
	√5

5(x+3)² + 5(y−6)² = 4x² + y² + 1 − 4xy − 2y + 4x x² + 4xy + 4y² + 26x − 58y + 224 = 0

P81: A no tak, dobra dzięki

ite: Dawno temu, jak jeszcze w szkołach średnich nie było rozszerzeń, to w programie były krzywe stożkowe (elipsa, parabola, hiperbola). Stąd wiedziałam, że jaką krzywą jest zbiór punktów równooddalonych od danego punktu i od podanej prostej. Ale do rysowania paraboli w geogebrze nie trzeba tego wiedzieć, ani korzystać z gotowej funkcji. Można to zrobić samemu: 1/ Narysuj podaną prostą i punkt A. 2/ Zaznacz na prostej dowolny punkt (u mnie B). 3/ Połącz je odcinkiem. 4/ Narysuj symetrlaną AB. 5/ Narysuj prostopadłą do podanej prostej przechodzącą przez B. 6/ Zaznacz ich punkt wspólny C. 7/ Pkt C → prawym klawiszem właściwości (podstawowe) → pokaż ślad https://www.geogebra.org/geometry/zvuuswkn

P81: Ok dzięki za ten poradnik − a mam jeszcze pytanie @ICSP teraz gdybym chciał wyznaczyć równania tych okręgów o środkach S(Xs,Ys) gdzie Ys= y ( wyznaczone z równania Paraboli to wtedy te równania mają postać (x−Xs)²+(y−Ys)²= r², co nie ? (Tylko że uzależnić drugą współrzędną środka okręgu od równania paraboli byłoby nieco trudno Tzn wyznaczyć y z równania x² + 4xy + 4y² + 26x − 58y + 224 = 0 )

ICSP: Słyszałeś kiedyś o równaniu kwadratowym?

P81: Tak,

P81: Ale czy mógłbyś to rozpisać bo nie ogarniam i tak jak wyznaczyć stąd y

ICSP: no to rozwiąż równanie kwadratowe albo ze względu na x albo ze względu na y. Uzależnisz dzięki temu odciętą od rzędnej albo rzędną od odciętej.

ICSP: x² + 4xy + 4y² + 26x − 58y + 224 = 0 4y² + y(4x − 58) + x² + 26x + 224 = 0 To jest nic innego jak równanie kwadratowe. Wypisz sobie współczynniki i podstaw do wzorów.

P81: No to ja tak samo zrobiłem tylko uzależniłem na odwrót no i mam ∆ = 440y−220 ale potem Wyjdą ciekawe pierwiastki jako y1 i y2

P81: Czyli potem wyjdą nam w sumie dwa równania okręgów ( jedno po jednym ramieniu paraboli a drugie po Drugim co nie ?)

ICSP: 1. Musisz się zdecydować czy wyznaczasz y w zależności od x (12:13) czy x w zależności od y(12:21) 2. Wyjdą dwie części paraboli ale to nie są okręgi.

P81: 1.Musisz się zdecydować..."" źle napisałem ale dobrze zrobiłem. 2. Tak, wiem − czyli te "y1 i y2" które otrzymam należy potem wstawić oddzielnie do równania √(−3−Xs1)²+(6−Y1)²= |−2x+Y1−1|/√5 − odległość środka od punktu (−3,6) jest równa odległości tego środka od prostej y = 2x+1 Oraz √(−3−Xs2)²+(6−Y2)²= |−2x+Y2−1|/√5 potem stąd wyznaczyć Xs1 oraz Xs2, potem obliczyć Y1, Y2 ( czyli drugą Współrzędną środka ) a następnie podstawić do wzoru r²= (−3−Xs1)²+(6−Y1)², analogicznie z drugim równaniem dla Xs2 i Y2 I to koniec, tak? Wtedy mamy równania tych wszystkich okręgów zapisanych jako Pierwszy przypadek gdy środki ich są na lewym ramieniu paraboli oraz Drugi przypadek gdy są na prawym, tak?

ICSP: y₁ , y₂ wyznaczasz właśnie z tego równania, więc jak je podstawisz to dostaniesz 0 = 0 Najpierw chciałeś wyznaczyć y w zależności od x − nie ma problemu Teraz nagle okazuje się, że te y podstawiasz do wyjściowego równania (bez jakiegoś większego pomysłu ani sensu).

P81: Czyli po wyznaczeniu y1, y2 co dalej mam zrobić ?

P81: Bo i tak na koniec ma wyjść 0=0 skoro jest ich nieskończenie wiele na jednym ramieniu paraboli jak i na drugimi

ICSP: Ja nie wiem co ty chcesz zrobić

P81: Cytuję "mam jeszcze pytanie @ICSP teraz gdybym chciał wyznaczyć równania tych okręgów o środkach S(Xs,Ys) gdzie Ys= y ( wyznaczone z równania Paraboli to wtedy te równania mają postać..." Chcę wyznaczyć po prostu równania tych okręgów Względem zamiennych, dlatego postanowiłem wyznaczyć y1, y2 ale nie wiem co teraz i zastanawiam się Czy jest sens bo i tak chyba wyjdzie 0=0 czyli liczyłem to bez sensu, tak?

ICSP: S(x₀ , y₀) − należy do równania paraboli wyznaczając y z równania paraboli dostajesz dwie funkcje: y₁(x) = ... y₂(x) = ...

	1
określone na pewnym zbiorze Δ ≥ 0 ( x0 ≤ −		chyba)
	4

r = √(x₀ + 3)² − (y₀ − 6)² równanie okręgu : (x − x₀)² + (y − y₀)² = (x₀ + 3)² − (y₀ − 6)²

	1
teraz y0 = y1(x0) lub y0 = y1(x0) dla x0 ≤ −
	4

i tyle. Dla różnych x₀ dostaniesz różne okręgi.

P81: Dziedzina tych funkcji x ≤ −¼ to się zgadza, Ale tutaj: r = √(x0 + 3)² − (y0 − 6)² tutaj nie powinno być plusa pomiędzy (x0+3)² a (y0−6)²? Liczymy odległość między Środkiem okręgu a punktem (−3,6) Bo resztę już rozumiem

P81: I tam powinno być y0= y1(x0) lub y0 = y2(x0) dla x0 ≤ − ¼ co nie ?

ICSP: tak powinien być + pod pierwiastkiem. tak powinno być y₂(x₀)

P81: Ok, dzięki wielkie za pomoc

P81: Wyszło, przesyłam jeszcze animację https://www.desmos.com/calculator/pbopuckvcf

P81: https://www.desmos.com/calculator/hymglgh1ap − jeszcze raz lekko spowolnione

Mila: P81 sam ułożyłeś to zadanie?

P81: tak

P81: @ICSP Mam jeszcze pytanie, bo na sam koniec przyjęliśmy okrąg o środku S(x₀, y₀ ) i względem tego uzależniliśmy y₁ =... oraz y₂ = ... od (x₀) , ale wcześniej wyznaczając równanie paraboli wzięliśmy pod uwagę jakiś punkt (x,y) i porównywaliśmy odległość tego punktu od punktu (−3,6) do odległości tego punktu (x,y) do prostej : √(x+3)² + (y − 6)² = |2x − y + 1|/√5 x² + 4xy + 4y² + 26x − 58y + 224 = 0 i tutaj mam pytanie, czy tutaj ten punkt o współrzędnych (x,y) to był też środek okręgu tylko dopiero potem zmieniliśmy na x₀ i y₀ lub czy liczyliśmy to dla dowolnego punktu który też się znajduje na tej paraboli a następnie wyznaczone y1 i y2 uzależniliśmy jako drugą współrzędną środka okręgu więc zamieniliśmy x na x₀ i y na y₀

P81: Osobiście mi się wydaje że wyznaczaliśmy równanie paraboli dla dowolnego punktu należącego do niej, ale chcę się upewnić

Mila: 1) Zbiór wszystkich punktów równo odległych od danej prostej i danego punktu nie leżącego na tej prostej jest parabolą. 2) x² + 4xy + 4y² + 26x − 58y + 224 = 0− równanie paraboli, jest to równocześnie zbiór środków wszystkich okręgów stycznych do danej prostej y=2x+1 przechodzących przez dany punkt P =(−3,6) nie leżący na tej prostej. 3) Tak dobrane dane spowodowały komplikacje w rachunkach i postać równania z którego możesz zobaczyć jaka to krzywa po obrocie ( i translacji ?) , wtedy otrzymasz równanie krzywej w postaci kanonicznej. 4) Jeżeli masz ochotę to znajdę zadanie podobne ale łatwiejsze. Wtedy zobaczysz jaka ładna parabolka wychodzi. Przekształcić równanie (2) ? Może po świętach.?

P81: √(x+3)² + (y − 6)² = |2x − y + 1|/√5 czyli tutaj współrzędne (x,y) to są współrzędne jakiegoś tam punktu dajmy na to P(x,y) który należy po prostu do tej paraboli i jest odległy od punktu (−3,6) o tyle samo jak do prostej y=2x+1, tak? I można to potraktować jako współrzędne środków okręgów tylko nazwane nie jako x0 i y0 tylko jako x i y? Inaczej mówiąc taka moja notatka : wyznaczamy równanie paraboli na której jest środek S(x0,y0) lub inny dowolny punkt (x,y) czyli √(x+3)²+(y−6)² = |−2x+y−1|/√5 , stąd x² + 4xy + 4y² + 26x − 58y + 224 = 0, następnie wyznaczamy x lub y czyli 4y² + (4x − 58)y+ x² + 26x + 224 = 0, liczymy deltę i mamy dwie proste y1 i y2 które uzależniamy od x0 czyli y1(x0) i y2(x0), gdzie x0 ≤ −0.25 no i potem już wiadomo co dalej

P81: Jeżeli masz ochotę to znajdę zadanie podobne ale łatwiejsze. Wtedy zobaczysz jaka ładna parabolka wychodzi. Przekształcić równanie (2) ? Może po świętach.? − nie nie trzeba, już mam trochę tego dosyć haha, męczy mnie ten temat o od kilku dni i rozwiązałem takich zadań już z 5 + 4 które sam wymyśliłem i na razie robię przerwę

Mila:

P81: A dałabyś Miła odpowiedzieć na moje pytanie 😅 godz 19:39

Mila: Po co to chcesz robić? Równanie x² + 4xy + 4y² + 26x − 58y + 224 = 0 jest równaniem paraboli ( z definicji) − zbiorem środków wszystkich okręgów stycznych do danej prostej i przechodzących przez dany punkt. Chyba nie rozumiem co jeszcze chcesz liczyć.

P81: Chodzi mi po prostu że podczas wyznaczania pierwszy raz równania paraboli to czy Tam x i y to były współrzędne środka okręgu tylko że potem ICSP przyjął współrzędne x0 i y0,. Nic nie chcę więcej Wyznaczać/ obliczać

P81: Chodzi mi o to że gdyby to były współrzędne okręgu to równanie paraboli było by takie x²₀ + 4x₀*y₀ + 4y²₀ + 26x₀ − 58y₀ + 224 = 0

P81: Chodzi mi czego to były współrzędne ( te x,y ) w równaniu √(x+3)²+ (y − 6)² = |2x−y+1|/√5 Skoro potem okręgu to x0 i y0 i uzależniamy y1 i y2 od x0

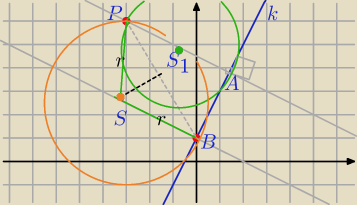
Mila: k: y=2x+1 m⊥k i P∊m

	1		9
m: y=−		x+
	2		2

	7		19
A=(		,		)− punkt styczności
	5		5

	8		49
S1=(−		,		) − środek jednego z okręgów spośród stycznych do k
	10		10

S=(x₀,y₀) −środek innego okręgu niż wyżej , SB⊥k |PS|=|BS| √(x₀+3)²+(y₀−6)²=r

	|2x0−y0+1|
r=
	√5

	|2x0−y0+1|
√(x0+3)2+(y0−6)2=
	√5

dla wygody piszemy dalej x, y otrzymując równanie krzywej drugiego stopnia .

P81: Ale po co wyznaczać punkt styczności i okrąg S1 skoro jest i tak on zawarty potem w jednym z tych równań https://www.desmos.com/calculator/hymglgh1ap , Ps. dobra i tak już chyba tamto zrozumiałem o co pytałem

Mila: Dla zrozumienia problemu. Można podstawić do otrzymanego równania krzywej i jeśli nie jest spełnione równanie, to oznaczałoby jakiś błąd w przekształceniach. Ufać − znaczy kontrolować!

P81: Czyli dla wygody piszemy dalej x, y otrzymując równanie krzywej drugiego stopnia . A potem wyznaczając stąd y1 i y2 dalej je uzależniamy od x₀ tak jak było w rzeczywistości na początku No ale tutaj pod linkiem https://www.desmos.com/calculator/hymglgh1ap Trzeba napisać równanie paraboli dla x i y ( nie dla wygody ) bo jeśli napiszemy Z x₀ i y₀ to wyjdą głupoty

P81: Tak samo jeśli napisalibyśmy równanie dodatkowe w tym kalkulatorze graficznym "y= (−4x+58 +− ✓−880x−220)/8 i tutaj dali zamiast "x", −> x₀ to nam wyjdzie funkcja liniowa Jakby z parametrem x₀

Mila: x² + 4xy + 4y² + 26x − 58y + 224 = 0 to jest szukany zbiór punktów wyrażony takim równaniem i jest to parabola . I kończę zadanie . Po co wyznaczasz y₁, y₂ ?

Mila: https://www.wolframalpha.com/input/?i=x%5E2+%2B+4xy+%2B+4y%5E2+%2B+26x+%E2%88%92+58y+%2B+224+%3D+0+

P81: ICSP : 2 kwietnia godz. 13:16... Żeby napisać równania tych okręgów, dobra już nie trzeba drążyć Tematu bo rozumiem po swojemu to

ICSP: Równanie: √(x+3)² + (y−6)² = |U{2x − y + 1}{√5| zostało napisane 2 kwietnia o 11:30 w odpowiedzi na wyznaczenie równania paraboli. Nie mogłem przewidzieć, że potem zechcesz wyznaczyć równania tych okręgów zależne od jednego parametru. Dlaczego wprowadziłem potem x₀ i y₀? Najprościej jest odpowiedzieć na to pytanie po prostu ich nie wprowadzając i zapisać równanie okręgu tylko za pomocą x i y: (x−x)² + (y−y)² = (x+3)² + (y−6)² gdzie x, y spełniają równanie: x² + 4xy + 4y² + 26x − 58y + 224 = 0 z ta pułapką, że nie każde x z powyższego równania są sobie równe i musisz wiedzieć który x spełnia równanie paraboli a który jest zmienną.

P81: Tak samo tutaj ( https://matematykaszkolna.pl/forum/408721.html ) jak robiłaś zadanie to na prostej ( dwusiecznej ) przyjęłaś jakiś punkt P(x,y) który Należy do dwusiecznej tak jak środek a nie od razu środek żeby nie pomieszać i dopiero później uzależniłaś od współrzędnych środka S(a,b) tak samo tutaj czyli wyznaczamy równanie paraboli na której jest środek S(x0,y0) lub inny dowolny punkt (x,y) czyli √(x+3)2+(y−6)2 = |−2x+y−1|/√5 , stąd x² + 4xy + 4y² + 26x − 58y + 224 = 0, następnie wyznaczamy x lub y czyli 4y² + (4x − 58)y+ x² + 26x + 224 = 0, liczymy deltę i mamy dwie proste y1 i y2 które uzależniamy od x0 czyli y1(x0) i y2(x0), gdzie x0 ≤ −0.25 no i podstawiamy (x − x0)² + (y − y0)² = (x0 + 3)² − (y0 − 6)², już wszystko rozumiem, chyba że chcesz coś dodać

P81: @ICSP rozumiem! Dzięki za potwierdzenie mojej teorii, Wesołych Świąt

P81: Jeszcze jedno "gdzie x, y spełniają równanie:" tutaj chodzi o tej x,y jako współrzędne środków okręgów? Albo inaczej mając to (x − x0)² + (y − y0)² = (x0 + 3)² − (y0 − 6)² ( gdzie x0,y0 spełniają równanie ) to wtedy równanie paraboli x²₀ + 4x₀*y₀ + 4y²₀ + 26x₀ − 58y₀ + 224 = 0, tak?

ICSP: tak.

Okip: A dlaczego jeśli się zmieni w tym równaniu paraboli x i y na x0 i y0 tak jak powinno być Na tej stronie z wykresami https://www.desmos.com/calculator/pdgqkcaivr To wtedy wgl nie jest rysowany wykres paraboli i jak się da Sam wykres y1= (−4x0+58−✓(−880x−220))/8 to wychodzi wykres funkcji liniowej Która się przesuwa góra dół − tak samo z y2 − skoro te funkcje przedstawiają drugą współrzędną środków Okręgów to powinno to przedstawiać jakby połowę paraboli i tutaj nie rozumiem, tego że skoro Ta strona odczytuje to jako że dla każdego X jest taka sama wartość ( jak się wejdzie W taką zębatkę i kliknie tabelka i tam to widać ) jakbyś mógł ICSP mi też na to odpowiedzieć Byłbym bardzo wdzięczny ( tylko zobacz ten wykres https://www.desmos.com/calculator/pdgqkcaivr ) Wygląda to tak jakby ta strona funkcję y1 = f(x0) rysowała w oddzielnym układzie współrzędnych

Okip: Albo jeśli Pan może, to niech sam na tej stronie napisze sam to jeszcze raz po swojemu i wyśle linka

ICSP: Strony nie znam, więc z nią nie pomogę.

Okip: Ale normalnie wykres funkcji y1= (−4x+58−✓(−880x−220))/8 Powinien się pokryć z wykresem y1= (−4x0+58−✓(−880x0−220))/8, prawda ? Niech Pan tylko zobaczy ten wykres żeby zrozumieć o co mi chodzi https://www.desmos.com/calculator/pdgqkcaivr Bo skoro ta strona wykres funkcji y1= (−4x+58−✓(−880x−220))/8 rysuje jako fragment paraboli a Funkcję y1= (−4x0+58−✓(−880x0−220))/8 na której leży środek jako linię prostą to coś jest nie tak, bo przecież środek leży na paraboli

ICSP: y jest funkcją stałą zależną od parametru x₀. Dla różnych x₀ dostajesz różne funkcje stałe np: y = 1 y = 3 itd.

Okip: To to już rozumiem w takim razie też bo wcześniej P81 pisał że jest to funkcja względem parametru x0, moje ostatnie już też pytanie dlaczego dla równania paraboli x²0 + 4x0y0 + 4y²0 + 26x0 − 58y0 + 224 = 0, Nie jest ona wgl rysowana na tej stronie tylko trzeba dać bez "0" przy y i x, no i wtedy wychodzi Poprawny wykres paraboli ( https://www.desmos.com/calculator/fzqn80iciy ) takie trochę to dziwne, Że parabolę która ma w swoim równaniu x0,y0 trzeba przedstawić jako x, y − reszta już mi się wyjaśniła, Tak wgl ciekawa z tego zadania wyszła rozmowa ( strasznie długa ), Jeśli jedynie wiesz jak na to odpowiedzieć to napisz a jeśli nie to już chyba kończę ten temat

ICSP: Ponieważ osie w układzie współrzędnych są jednoznacznie oznaczone. Nie możesz raz używać x, raz x₀ itd. Nie możesz narysować w układzie w jednym układzie współrzędnych funkcji raz zależnej od x a raz zależnej od x₀.

Okip: To rozumiem, że dlatego np funkcję y1= (−4x+58−✓(−880x−220))/8 a y2= (−4x0+58−✓(−880x0−220))/8 rysuje inaczej bo są osie x i y natomiast x0 traktuje jako parametr Ale równania paraboli w takiej postaci z x0 i y0 wgl nie rysuje natomiast tamte y1 i y2 rysuje ich szkic https://www.desmos.com/calculator/8vnfxm7phi

ICSP: postać parametryczna:

	1
(x0 , f(x0)) , x0 ≤ −
	4

i powinno narysować

Anonim: Ja też już mam mętlik w głowie jak P81 od tego, mógłbyś ICSP jeszcze raz wytłumaczyć to wszystko? Tylko dla okręgów o środkach S(a,b)... najpierw podczas wyznaczania mamy równanie paraboli z a i b ale do kalkulatora graficznego trzeba zamienić na x i y,( dlaczego ?), potem się wyznacza y1 i y2 czyli funkcję których suma jest parabolą itd, następnie jak się uzależni drugą współrzędną środka od y1/y2 to niby te środki leżą na paraboli ale wstawiając to do kalkulatora graficznego w zmiennych a/b, rysuje to jako funkcję parametryczną

Anonim: ICSP Czyli można to zrobić tak jak Mila tutaj https://matematykaszkolna.pl/forum/408721.html żeby najpierw wyznaczyć równanie paraboli dla jakiegoś punktu również należącego do paraboli np A(x,y) stąd równanie : x² + 4xy + 4y² + 26x − 58y + 224 = 0, a dopiero potem jak już się stąd wyznaczy y1(x) i y2(x) to żeby uzależnić to jako współrzędną środka okręgu np S(a,b) stąd mamy dwa przypadki środków okręgów ( zależy na którym są ramieniu paraboli ) S(a, (−4a+58−√(−880a−220))/8 ) Lub S( a, (−4a+58−√(−880a−220))/8 ), gdzie a ≤ ¼ ...