kielbasa kozak123: Funkcja f określona jest wzorem ( x2 + mx + 1 dla x < 2 f(x) =( −3x−9 dla x≥2 Znajdź te wartości parametru m, dla których funkcja m jest malejąca. mam problem z tym zadaniem i nie moge go rozwiazac, bo funkcja maleje do wierzcholka, potem

	−m
rosnie a potem znow maleje, wiec m mozna szukac w		>=2
	2

ale nie rozumiem drugiego warunku, dlaczego funkcja paraboli w 2 musi być większa niż ta funkcja malejąca w 2

Jerzy: Sprawdź dokładnie , czy dobrze przepisałeś treść, bo tutaj nie istnieje takie m.

ICSP: bo jeżeli będzie mniejsza to funkcja będzie malejąca przedziałami a nie w całej dziedzinie. Patrz definicja monotoniczności funkcji.

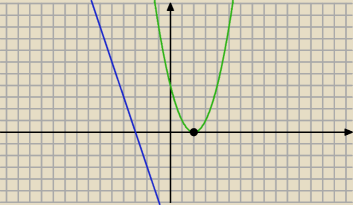
Jerzy: Dla m = −2 funkcja jest malejąca w całej dziedzinie

etna: Jakie powinny być nawiasy przy zapisie przedziałów monotoniczności? Dlaczego? Pytanie wynika stąd, że w w starych podręcznikach (zbirach zadań) przedziały monotoniczności są zapisywane jako otwarte np. dla f. kwadratowej f(x) = x² funkcja jest malejąca dla x ∊ (−∞; 0) oraz rosnąca dla x ∊ (0, +∞). Obecnie (w nowych podręcznikach) końce przedziałów są domknięte, np. dla f. kwadratowej f(x) = x² funkcja jest malejąca dla x ∊ (−∞; 0> oraz rosnąca dla x ∊ <0, +∞). Dlaczego tak jest? Przecież przy nawiasach ostrych dla zera funkcja jednocześnie jest i malejąca i rosnąca. Dla mnie to sprzeczność. Gdzie robię błąd?

sad: Ja mam ten sam problem! Co z końcami przedziałów?

Jerzy: To wynika z faktu,że trudno jest mówić o monotoniczności funkcji ciągłej w punkcie, dlatego obydwa zapisy

	1
są poprawne. Ale np. funkcja f(x) =		jest monotoniczna w przedziałach (−∞,0) oraz (0,∞)
	x

, bo nie jest ciągła w punkcie x = 0.

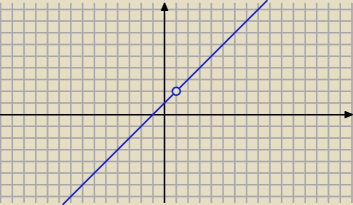
Jerzy: Funkcja jest rosnąca w całej dziedzinie pomimo,ze x = 1 nie należy do dziedziny

etna: I poprawiający na maturze uznają obydwa zapisy?

ABC: co roku te same dyskusje w maju https://matematykaszkolna.pl/forum/16121.html

Jerzy: Tak jak "odgrzewany stary kotlet" : czy dla Δ = 0 trójmian ma jedno, czy dwa miejsca zerowe ?