monotoniczność wrrrrrrrrr: mam pytanie... wiem pewnie się powtórzy... ale piszę już w środę maturę... i ciągle się mylę bo róznie widzę... chodzi o monotoniczność czemu nieraz pisze się nawias domknięty a nieraz otwarty czy tak i tak uznają mi na maturze (link niżej wszystko wyjaśni) tu akurat przy − 2 jest domknięty matematyka.pisz.pl/strona/1483.htmlodpowiedz ale nieraz pisze się otwarty kiedy?

tim: Więc tak. Przyjęte jest (na maturze) jeżeli masz podane przedziały monotoniczności to otwarte, jeżeli zaś maksymalneprzedziały monotoniczności to domknięte, chyba, że wyklucza je dziedzina.

wrrrrrrrrr: aha czyli jak by byla np. taka sinusoida to pisze np. rosnąca (−3, 3) malejąca (3,2) rosnąca (2, 5) podałamprzykladowe liczby

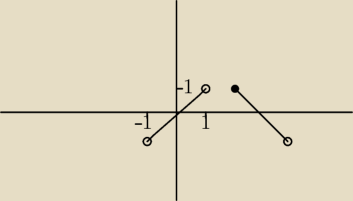
imię lub nick: może lepiej inny przykład: załóżmy że mamy funkcję: y=x dla x∊(−1;1) y=−x dla x∊<2;4) wtedy: funcja jest rosnąca w przedziale (−1;1) malejąca w przedziale <2;4) roxzumiesz?

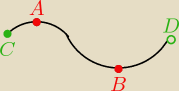
♊: Jemu chodzi o taki przykład . . . Są 2 możliwości jednakowo poprawne zapisu tego. 1. Funkcja rosnąca w przedziale <C,A) oraz (B,D) i malejąca w (A,B) 2. funkcja rosnąca w przedziale <C,A> oraz <B,D) i malejąca w <A,B> Małe wyjaśnienie − te nawiazy pogrubione muszą być zawsze (bo funkcja po nich się kończy) Te nawiasy podkreślone można stosować zamiennie. Ale jeżeli już stosujesz jednych to stosujesz ich cały czas, nie możesz tosować raz tak raz tak, bo tak Ci wygodniej. Więcj jeżeli napisał(a)byś, że funkcja rośnie w przedziale <C,A> i maleje w (A,B) i znowu rośnie w <B,D) to masz błąd. Jak ja zdawałem maturę to były możliwe obie wersje, ale trzeba było zdecydować się na jedną i tą stosować przez cały egzamin.

imię lub nick: teraz też powinny być możliwe dwie wersje. im chodzi jedynie o to żeby nie podawać niekompletnych przedziałów. np. funkcjia y=x jest rosnąca w całej swojej dziedzinie ale jak podamy że jest rosnąca w przedziale (−1;1) to nie jest to nieprawdą

♊: Aj! Potem wywaliłem dalszą częśc mojej wypowiedzi. Ogólnie nie ma jedynej słusznej metody, bo do tej pory najtęższe mózgi matematycznego świata nie doszły do porozumienia w trakcie żarliwych dysput na ten temat (cytat z jednej z nich zamieszczam poniżej: ___________________________________________________________________________________ <prof A> To mają być przedziały Zamknięte ! Z−A−M−K−N−I−Ę−T−E ! ! ! <prof B> OTWARTE ! Zamknąć to Ty się możesz. <prof C> Ja lubię chomiki ! C − H − O − M − I − K − I ! ! ! ___________________________________________________________________________________ _{oczywiście nie bierzcie tego "cytatu" aż tak dosłownie ;P}