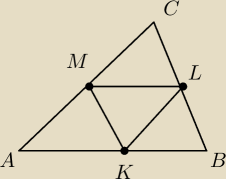
prosze o pomoc anka: Wyznacz współrzędne wierzchołków trójkąta ABC, jeżeli punkty K=(− 1, −2), L=(−5, −3), M=(−2,−5) są środkami jego boków.

jc:

	1
K=		(A+B)
	2

	1
L=		(B+C)
	2

	1
M=		(C+A)
	2

A= K+M−L B=K+L−M C=L+M−K

Saizou :

	xa+xb		ya+yb
K = (		,		)
	2		2

	xb+xc		yb+yc
L = (		,		)
	2		2

	xa+xc		ya+yc
M = (		,		), zatem
	2		2

	xa+xb
−1 =		⇒ −2 = xa+xb
	2

	xb+xc
−5 =		⇒ −10 = xb+xc
	2

	xa+xc
−2 =		⇒ −4 = xa+xc
	2

Wyznacz x_a, x_b, x_c Analogicznie dla y.

piotr: równanie okregu przez K, L, M. (x + 63/22)² + (y + 67/22)² = 1105/242 jest okrąg wpisany w trójkąt ABC styczne do okręgu w punkcie K: y = −(41 x)/23 − 87/23 w punkcie L: y = 47 x + 232 w punkcie M: y = (19 x)/43 − 177/43 Punkt A na przecięciu prostych: y = −(41 x)/23 − 87/23 i y = 47 x + 232 x = −29/6, y = 29/6 Punkt B na przecięciu prostych: y = 47 x + 232 i y = (19 x)/43 − 177/43 x = −71/14, y = −89/14 Punkt C na przecięciu prostych: y = −(41 x)/23 − 87/23 i y = (19 x)/43 − 177/43 x = 3/20, y = −81/20

piotr: Przepraszam, zrobiłem źle.

Mila: https://matematykaszkolna.pl/forum/408625.html