Dowodzenie JAN: Witam.. Czy ktoś z Państwa umie rozwiązać to zadanie? https://zapodaj.net/a3ff5e87d0c43.png.html>

ICSP: https://matematykaszkolna.pl/forum/407953.html

ICSP: Sprawdź posty z dnia wczorajszego z godziny około 21. Były podane trzy różne rozwiązania.

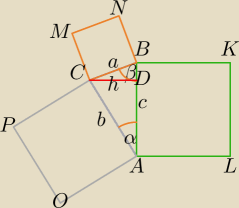
Mila: Dane:

	5
tgα+tgβ=		, ( *) 5*PΔABC=c2
	2

Wykazać , że : a²+b²=5*P_ΔABC ================

	sinα		sinβ		sin(α+β)
1) tgα+tgβ=		+		=
	cosα		cosβ		cosα*cosβ

sin(α+β)		5
	=		⇔
cosα*cosβ		2

	5
(**) sin(α+β)=		cosα*cosβ
	2

2)

1		c2		2c
	c*h=		⇔h=
2		5		5

	|AD|
W ΔCDA: cosα=		⇔|AD|=b*cosα
	b

	|BD|
w ΔCDB: cosβ=		⇔||BD|=a*cosβ
	a

3)

	1		1		1
PΔACB=		*a*b*sin C=		a*b*sin(180−(α+β))=		a*b*sin(α+β)
	2		2		2

Korzystając z (*) i (**)

1		c2		5		2c2
	a*b*sin(α+β)=		⇔a*b*		cosα*cosβ=
2		5		2		5

	4c2
a*b*cosα*cosβ=		⇔ ( z zależności w Pkt. (2) )
	25

|AD|*|BD|=h²⇔ |∡C|=90^o 4) a²+b²=c² czyli a²+b²=5*P_ΔABC

qstosz: Bardziej już się chyba nie dało zagmatwać. Przez takich nauczycieli gmatwających proste zadania obrzydza się matematykę

ABC: nie krytykuj , po prostu pokaż jak to zrobić lepiej

qstosz: Nie ma co pokazywać, to zadanie było już na tym forum wielokrotnie pokazywane, nie zauważyłeś ABC ?

ABC: ja pracuję na dwa etaty, nie mam czasu śledzić dokładnie zadań na forum

qstosz: to twój problem, a więc się nie czepiaj, a zadanie jest proste i wyszukaj na forum różne proste rozwiązania tego zadania, albo sam spróbuj znaleźć jak najprostsze rozwiązanie i dopiero potem zabieraj glos

ABC: dobrze , poczekam aż ty coś rozwiążesz malkontencie, oby to było proste i przejrzyste bo też cię tak skrytykuję

πes: I jak ? gdzie tradycyjna emotka

qstosz:

φga: