zadania przygotowujące do matury na poziomie rozszerzonym
Damian#UDM: PR ZADANIA MATURALNE PR
1. (0−3) OE P 2021 2
Suma kwadratów liczb naturalnych a i b jest równa kwadratowi liczby naturalnej c. Wykaż, że
jeśli liczba c jest o 1 większa od liczby b, to liczba b jest podzielna przez 4.
Moja próba:
a, b, c ∊ N
c = b + 1
a
2 + b
2 = c
2 → a
2 + b
2 = (b + 1)
2 → a
2 + b
2 = b
2 + 2b + 1 → a
2 = 2b + 1
| | a2 − 1 | | (a−1)(a+1) | |
b = |
| = |
| , w tym momencie stwierdziłem, że zobaczę co się dzieje dla |
| | 2 | | 2 | |
liczb parzystych oraz nieparzystych.
dla a=2n, n∊N
| | (2n−1)(2n+1) | |
b = |
| = 2n2 − 12 , czyli nie wyszła mi liczba naturalna, więc coś jest |
| | 2 | |
źle.
dla a=2n+1 , n∊N
| | (2n)(2n+2) | |
b = |
| = 2*n*(n+1) , tutaj mam iloczyn liczby 2 oraz dwóch kolejnych liczb, z |
| | 2 | |
których jedna jest na pewno parzysta, więc liczba b w tym przypadku jest podzielna przez 4.
Co robię źle? Zapraszam do dyskusji

24 lut 01:41
Adamm: pyrrr
24 lut 01:52
Adamm: b naturalne to 2|(a−1)(a+1). Więc 2|a−1, a+1 przy czym 4|a−1 lub 4|a+1
24 lut 01:56
Adamm: co robisz źle? wnioski
24 lut 01:57
chichi:
Jakie kuźwa przypadki jak widać od razu... z postaci a2=2b+1, że 2b+1 jest nieparzyste dla
dowolnego b∊N, więc a2 również musi być nieparzyste, zatem niech a=2m+1, m∊N i mamy:
(2m+1)2=2b+1 ⇒ 4m2+4m+1=2b+1 ⇒ 2m(m+1)=b=4k, k∊N Q.E.D.
24 lut 03:03
chichi:
Z mojego uzasadnienia już widać dlaczego masz sprzeczność w przypadku dla 'a' parzystego

24 lut 03:10
Filip:
Jakie kuźwa
Q.E.D − jesteśmy w Polsce (przynajmniej ja), używa się
c.n.u / c.n.w i
wiele innych

Przy okazji witam

24 lut 08:46
chichi:
Hej, no wielu innych czyli m.in.
Q.E.D. to, że ty używasz
c.n.u. to znaczy, że ja mam
używać? Ale jak to, ktoś robi inaczej niż z ja..

24 lut 09:53
6latek: Ja w ksiazce mam
c.b.d.u
Fakt nie wiem co to jest
Q.E.D
Jesli z angielska to nie zasmiecajmy naszego pieknego jezyka tymi nalecialosciami

24 lut 09:59
chichi:
Kto jak kto, ale, że ty @
6latek nie znasz tego skrótu, to mnie zaskoczyłeś
Q.E.D. −
quod erat demonstrandum, zwrot pochodzący z łaciny, a tego, że masz czas pisać swoje
przypuszczenia na forum, a nie masz czasu wpisać w google q.e.d. i poczytać, to już nie
rozumiem. Nie zasmiecajcie tematu, pozdrawiam

24 lut 10:07
6latek: Pozdrawiam

dziekuje za wyjasnienie .
Tak naprawde to znam tylko rosyjski . Uczyli tylko wtedy tego języka .
24 lut 10:10
6latek: Niedobre czasy nastaly. Wszyscy wszystkich odsylaja jak nie na google to do wiki
Nikt juz spokojnie nie potrafi wytlumaczyc bez jakiejkolwiek zlosliwosci

24 lut 11:30
Damian#UDM: 6latek zgadzam się z Tobą. Niestety nic z tym nie zrobisz.
Dziękuję za wyjaśnienie, myślałem, że założenia zadania mają być spełnione dla liczb parzystych
oraz nieparzystych, a jak widać z rozwiązania chichi tak niekoniecznie zawsze musi być.
24 lut 13:13
Saizou :
Polecam pisać czarny kwadracik i nie będzie problemu

24 lut 13:53
Eta:
A ja polecem pisać :
c.n.w lub c.n.u

24 lut 13:56
Jerzy:
c.n.d. , też stosowany zapis

24 lut 13:58
Eta:
Hej
Jerzy 
kiedyś też używaliśmy c.b.d.o lub c.b.d.u
"co było do okazania" , "co było do udowodnienia"
24 lut 14:35
Adamm:
równie dobrze można pisać "KONIEC" na końcu dowodu
24 lut 14:53
Adamm:
ja osobiście albo nic nie piszę, albo maluję kwadraciki
polecam sobie narysować ze 20, działa terapeutycznie
24 lut 14:57
:)))): Dziwne, że jeszcze nikt nie wymienił c.k.d ,,co kończy dowód''
24 lut 14:59
Słoniątko:
najlepszy jest dowód przez zastraszenie :
albo uwierzycie na słowo, albo będę trzy godziny dowodzić
można też przez odwołanie się do sił nieczystych:
a diabli wiedzą jak to udowodnić
24 lut 15:16
BoosterXS: Co to za arkusz?

24 lut 15:37
Saizou :
OE = oficyna edukacyjna
P − poziom podstawowy
24 lut 15:39
ICSP: albo dowód typu ł.w.
24 lut 15:43
chichi:
@
Saizou w tytule jest napisane "zadania przygotowujące do matury na poziomie
rozszerzonym", poza tym dowód IMO za 3 pkt. to. rzadko kiedy na podstawie i to nie ten poziom
zadania, na podstawie co najwyżej zwinięcie do wzoru skróconego mnożenia

24 lut 18:16
Qulka: ja uwielbiam pisać c.d.n czyli "co dowieść należało "

24 lut 18:20
Adamm: i tak to bez znaczenia jak się nie jest nauczycielem albo się książek nie czyta
24 lut 19:23
Jerzy:
c.d.n. , ciąg dalszy nastąpi ( w serialach )
24 lut 21:36
24 lut 22:40
24 lut 23:19
Damian#UDM: P oznacza Pazdro.
25 lut 01:13
Adamm: @ite dowód całkowy
25 lut 02:03
Damian#UDM: 2. (0 − 2) OE P 2021
Liczby a, b, c są długościami boków trójkąta. Pokazać, że a2 + b2 + c2 < 2*(b + c)2
25 lut 19:16
Filip:
a2 < b2 + c2 + 4bc
b2 + c2 − 2bccosα < b2 + c2 + 4bc
−cosα < 2
25 lut 19:24
Damian#UDM:
a
2 < b
2 + 4bc + c
2
25 lut 19:25
Eta:
a<b+c −− z nierówności trójkąta
to a2<(b+c)2
zatem...........
25 lut 19:29
ICSP: L = a2 + b2 + c2 < (b+c)2 + b2 + c2 = (b+c)2 + (b+c)2 − 2bc < 2(b+c)2 = P
25 lut 19:31
Eta:

25 lut 19:32
Damian#UDM: a2 < (b+c)2
a2 + b2 + c2 < (b+c)2 + (b+c)2
b2 + c2 < (b+c)2
b2 + 2bc + c2 > b2 + c2
2bc>0 , bo b>0 oraz c>0
jest ok ?
25 lut 19:33
ICSP: Strasznie słaba ta nierówność.
Śmiało mogę dwa razy postawić < zamiast chociaż raz ≤
25 lut 19:33
ICSP: Jest fatalnie.
Ja nie mogę się zorientować co tam po kolei robisz.
Osoba która będzie sprawdzała twoją maturę nie będzie się zastanawiała jakie przekształcenie
zostało wykonane jeżeli nie będzie ono dość oczywiste.
25 lut 19:36
Damian#UDM: Rozumiem, a czy jeśli z nierówności trójkąty wiemy, że
a < b+c to a2 < (b+c)2
to wystarczy, że z nierówności
a2 + b2 + c2 < 2*(b+c)2
pokaże, że b2 + c2 < (b+c)2 jest spełnione i zadanie jest wykazane?
25 lut 19:38
ICSP: Dlaczego zakładasz, że to co wykazujesz jest prawdą?
Wykazujesz pewną nierówność − nie możesz jej używać od tak sobie w dowodzie.
Jeżeli już z pewnych względów musisz to jest coś takiego jak dowód niewprost lub metoda
przekształceń równoważnych.
25 lut 19:41
Damian#UDM: Najbardziej mi się podoba rozwiązanie za pomocą twierdzenia cosinusów

Wyżej 25 lut 19:38 zakładam, że z nierówności trójkąta tak jak
Eta napisała
a < b + c ⇔ a
2 < (b+c)
2
i to jest na pewno prawdziwe, więc pytam się czy jeśli wiem, że nierówność wyżej jest prawdziwa
to czy w nierówności
a
2 + b
2 + c
2 < (b+c)
2 + (b+c)
2 pokaże, że b
2 + c
2 < (b+c)
2 jest też prawdziwe to czy
zadanie będzie prawidłowo wykonane?
A rozwiązanie b
2 + c
2 < (b+c)
2 przedstawiłem w 25 lut 19:38
25 lut 19:50
Damian#UDM: przedstawiłem w 25 lut 19:33
25 lut 19:51
ICSP: Skąd masz tą nierówność:
a2 + b2 + c2 < (b+c)2 + (b+c)2 ?
25 lut 19:53
Damian#UDM: Z treści zadania, rozpisałem prawą stronę z iloczynu na sumę.
25 lut 19:57
ICSP: Nie rozumiesz.
Skoro masz udowodnić pewną nierówność to nie możesz z niej wcześniej korzystać
(wyjątkiem jest np. metoda przekształceń równoważnych albo dowód niewprost)
jest to poważny błąd logiczny za który raczej dostaje się 0 pkt za zadanie.
25 lut 20:04
6latek: a<b+c to a2<(b+c)2
b<a+c to b2<(a+c)2
c<a+b to c2<(a+b)2
=========================
a2+b2+c2<(b+c)2+(a+c)2+(a+b)2
a2+b2+c2<(b2+2bc+c2)+(a2+2ac+c2)+ (a2+2ab+b2)
a2+b2+c2<2a2+2b2+2c2+ 2ab+2bc+2ac
Co dalej zrobic?
25 lut 20:07
Eta:
a<b+c
a2<(b+c)2 | +b2+c2
a2+b2+c2<(b+c)2+b2+c2 < (b+c)2+b2+c2+2bc = (b+c)2+(b+c)2=2(b+c)2
25 lut 20:19
6latek: OK. Rozumiem .
25 lut 20:23
Damian#UDM: Ja również już rozumiem. Dziękuję za wyjaśnienia

25 lut 20:48
Eta:

25 lut 20:52
25 lut 20:55
Damian#UDM: dziękuję
Eta 
kochana jesteś! Pozdrawiam serdecznie

25 lut 20:56
Damian#UDM: (0−5)
https://drive.google.com/drive/folders/1UyCWF8p4RFQF-6j-bJ10ZtIlqZVR2G-A?usp=sharing
W trapezie ABCD dwusieczna kąta przy wierzchołku B, przecina przekątną AC w punkcie P, a
krótszą podstawę CD w punkcie
E (zobacz rysunek). Wiedząc, że |AB| = 15, |BC| = 9 oraz pole
trójkąta ABP jest równe polu powierzchni czworokąta APED,
oblicz długość odcinka DE.
|DE|=x, |CE|=y, x>0, y>0
Δ
ABP ≈ Δ
PCE → (kkk)
|∠ABP|=|∠PEC|=α
|∠BAC|=|∠PCE|=β
m=|PS|, S∊AB
k=|PL|, L∊CD
m>0, k>0
m+k=h
ABCD=|LS|=|PS|+|PL|, m>k, h>0
| | 15*m | |
PΔABP=PAPED=12*15*m= |
| |
| | 2 | |
| | 15*m | | (15+x) | |
P{ABED}=2* |
| =15*m= |
| *h |
| | 2 | | 2 | |
Nie wiem co dalej, proszę o pomoc

26 lut 01:45
Qulka: jeszcze było słowo dwusieczna.....
więc AP : PC= .....
więc masz skalę podobieństwa

26 lut 08:35
Qulka: mi wyszło x=15/4
26 lut 08:48
Eta:
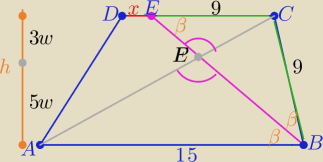
1/ z własności dwusiecznej ΔBCE równoramienny
to |EC|=|BC|=9
2/ Z podobieństwa ΔABP i EPC (z cechy (kkk)
Punkt P dzieli wysokość na odcinki 3w i 5w
P(ABED)= 2P(ABP) −− z treści zadania
zatem
..............
==========
26 lut 11:25
ICSP: Nie wiem dlaczego jedna z najstarszych dziedzin nadal jest na maturze

26 lut 11:55
Eta:
Planimetria jest piękna, uczy myślenia i odbiega od schematów

26 lut 14:49
Damian#UDM: Racja, Δ równoramienny, nie zauważyłem tego. Dziękuję za pomoc
Eta oraz
Qulka 
26 lut 15:24
Damian#UDM: Myślałem, że będzie więcej problemów z tymi arkuszami, lecz jak na Pazdro to nie były takie złe

26 lut 15:41
Damian#UDM:
7. (0−3)
https://drive.google.com/drive/folders/1UyCWF8p4RFQF-6j-bJ10ZtIlqZVR2G-A?usp=sharing
Przekątne AC i BD równoległoboku ABCD przecinają się w punkcie S. Przekątna BD jest
prostopadła do boków AD i BC, a |∡BAD| = |∡BSC| (zob. rysunek).
Udowodnij, że |AB| = |AD|*
√3.
W tym zadaniu znalazłem trójkąty podobne oraz wyznaczyłem wszystkie kąty, lecz nie mam pomysłu
jak dojść do podanej tezy.
Zadanie 15. (0−7) (treść zadania na dysku w linku wyżej)
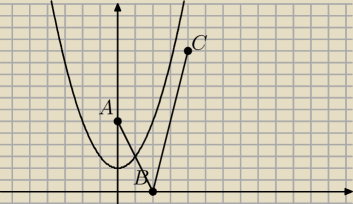
b) Wyznacz dziedzinę funkcji f.
c) Wyznacz współrzędne takiego punktu P, dla którego funkcja f osiąga wartość najmniejszą
Zastanawiam się jak wyznaczyć dziedzinę funkcji f. Punkt ma leżeć wewnątrz kąta. Narysowałem
sobie podaną sytuację.
Czy to oznacza, że x ∊ (1,3) ? Szczerze mówiąc nie mam pomysłu jak to algebraicznie wyznaczyć.
Proszę o wskazówki oraz pomoc

1 mar 15:35
ICSP: Wyznacz równanie prostej BC i sprawdź w jakim punkcie przetnie się ona z parabolą.
Jeśli się nie przetnie to x możesz wziąć dowolnie duże.
Od dołu oczywiście musi być x = 1
1 mar 15:51
Saizou :
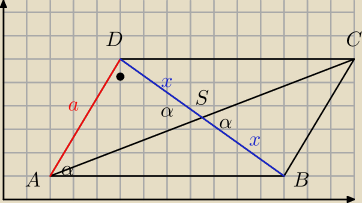
∡ASD = α
ΔABD ~ΔSAD (kkk)
a
2 =2x
2
2x =
√2a
Z tw. Pitagorasa w ABD
|AB|
2 = a
2 + (
√2a)
2 =3a
2
|AB| = a
√3 = |AD|
√3
1 mar 15:55
Qulka:
zadanie 7
| a | | 2x | |
| = |
| więc a2=2x2 zatem x=a/√2 |
| x | | a | |
i z większego pitagoras b
2=a
2+4x
2 więc b=a
√3
1 mar 15:56
Damian#UDM: BC: y=6x−12
Punkt wspólny prostej BC oraz y=x2+2
x2+2=6x−12
x2−6x+14=0
(x−3)2+5=0
Brak punktów wspólnych, zatem dziedzina funkcji jest równa Df=(1,+oo)
1 mar 16:00
Damian#UDM: Dziękuje
Qulka oraz
Saizou za pomoc, teraz już wszystko rozumiem

Oraz ICSP za
cenną wskazówkę

1 mar 16:02
Damian#UDM: (0−6) ON 2020 PR
| | 4−m | |
Dla jakich wartości parametru m funkcje f(x)= |
| oraz g(x)=x2+5x+m, dla x≠0, mają |
| | x | |
dokładnie trzy punkty wspólne?
Jeśli funkcje f(x) oraz g(x) mają punkty wspólne, to można je do siebie przyrównać
f(x)=g(x)
4−m=x
3+5x
2+mx
x
3+5x
2+mx+m−4=0
No i co dalej to nie wiem

Szukałem miejsc zerowych tego równania lecz nie mogę znaleźć.
Proszę o pomoc

2 mar 13:06
?: To trzeba lepiej szukać

x
3 + 5x
2 + mx + m − 4 = x
3 + x
2 + m(x + 1) + 4x
2 − 4 = x
2(x + 1) + m(x + 1) + 4(x
2 − 1)
= x
2(x + 1) + m(x + 1) + 4(x − 1)(x + 1) =
= (x + 1)(x
2 + m + 4(x − 1)) = (x + 1)(x
2 + m + 4x − 4) =
= (x + 1)(x
2 + 4x + m − 4)
Teraz lepiej?
2 mar 13:19
chichi:
Zastanawia mnie jak szukasz miejsc zerowych (pokaz jak je szukałeś) jak od razu widać... Niech
W(x)=x
3+5x
2+mx+m−4, to
W(−1)=−1+5−m+m−4=0 
2 mar 13:19
Damian#UDM: Dobra, w głowie podstawiałem przy m też −1 i mi wychodziło −2...
Wszystko jasne, dziękuję

2 mar 14:31
Damian#UDM: Teraz dalej, jak równanie
x
2+4x+m−4=0 musi mieć dwa rozwiązania, czyli Δ>0.
Δ=16−4*(m−4)=16−4m+16=32−4m=4*(8−m)
8−m>0 ⇔ m<8
m∊(−
∞,8)
I to jest wszystko? Za to jest aż 6 punktów?

chyba jeszcze przyda się warunek x
2≠−1 oraz x
3≠−1

2 mar 14:42
wędkarz: jak się dobrze poszuka, to się znajdzie....ale lepiej iść na ryby

2 mar 14:47
Eta:
Dla x2+4x+m−4=0
Δ>0
f(0)≠0
f(−1)≠0
2 mar 14:52
Damian#UDM: Eta czy mogłabyś mi wytłumaczyć z czego wynikają podane przez Ciebie warunki?
2 mar 15:03
chichi:
A no pierwiastki muszą być rózne, więc jeśli jeden pierwiastek to (−1) to dwa pozostałe muszą
być od niego różne, a drugi warunek widać już w pierwszym przyrównaniu, zobacz co się dzieje
| | 4−m | |
dla m=4 tutaj: |
| =x 2+5x+m, czy otrzymamy 3 różne rozwiązania?  |
| | x | |
2 mar 15:07
Damian#UDM: chichi no wtedy otrzymamy tylko 2 rozwiązania

2 mar 15:37
ICSP: Rozwiązania muszą:
1o muszą być dwa i do tego różne
2o muszą być różne od −1
3o muszą należeć do dziedziny
Przyporządkuj sobie strzałeczkami podpunkty 1o−3o do warunków które podała Eta.
2 mar 16:01
Damian#UDM: Chyba już rozumiem, dziękuję wam za pomoc

2 mar 16:15
Damian#UDM: (0−5) PR
Dodatnie liczby wymierne a, b spełniają równość
a3 + 4*a2*b = 4*a2 + b4
Udowodnić, że liczba √a−1 jest kwadratem liczby wymiernej.
4 mar 21:48
Eta:
a
3+4a
2b=4a
2+b
4 /
+4ab2
.......................................
otrzymujemy:
a(a+2b)
2 −(2a+b
2)
2=0
rozkładajac na czynniki:
[
√a(a+2b)−2a−b
2]*[
√a(a+2b)+2a+b
2]=0
=============== sprzeczność, bo a,b>0
zatem równanie:
b
2−2
√a*b +2a−a
√a=0 ma ze względu na"b"rozwiązania wymierne
gdy Δ
b =k
2 −− jest kwadratem liczby k
Δ
b= (2
√a)
2−8a+4a
√a = 4a(
√a−1)
k
2=4a(
√a−1)
i mamy tezę
√a−1= t
2, t∊W
=============
5 mar 15:57
Kacper:
Ja mam skojarzenie ze skrótem c.n.d = co należy dokończyć

5 mar 17:38
Eta:
Ja też

"ciąg dalszy nastąpi "
5 mar 17:40
Damian#UDM: Ja tu myślałem o wyciąganiu przed nawias, a widzę, że trzeba było myśleć o dodaniu czegoś

Jestem w szoku, chciałbym widzieć tak szybko rozwiązania i pomysły jak wy

Pozdrawiam was kochani!
5 mar 21:54
Damian#UDM: Zapisz w postaci iloczynu wyrażenia
1. cos(α) + cos(5α) + cos(9α)
2.
√3 − 2sin(α)
proszę o pomoc

9 mar 20:01
Saizou :
| | x+y | | x−y | |
1) skorzystajmy ze wzoru na cosx+cosy = 2cos |
| cos |
| , zatem |
| | 2 | | 2 | |
| | x+9x | | x−9x | |
cosx+cos(9x) + cos(5x) = 2cos |
| cos |
| + cos(5x) = |
| | 2 | | 2 | |
= 2cos(5x)cos(−4x)+cos(5x)=cos(5x)(2cos(4x)+1)
9 mar 20:07
Saizou :
2) hmm... co tutaj chcesz przedstawić w postaci iloczynu? I w jakim celu?
9 mar 20:11
ICSP: Taka jest pewnie treść zadania
| | π | |
√3 − 2sinx = 2(sin( |
| ) − sinx) |
| | 3 | |
i wzór na różnicę sinusów.
9 mar 20:13
Damian#UDM: Zaraz wrzucę tutaj link do dysku z treścią zadania, żeby nie było

W pierwszy zsumowałem najpierw cos(α) oraz cos(5α) no i dlatego nie wyszło mi

A na drugie aż tak daleko na ten pomysł nie wpadłem. Dziękuję wam za pomoc

9 mar 21:13
chichi:
Brak doświadczenia

9 mar 21:17
Damian#UDM: Dziękuje chichi za motywację do dalszych działań

9 mar 23:13
9 mar 23:18
ello:
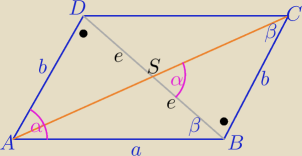
zad 7/
ΔABD ∼BCS z cechy (kkk)
z tw. Pitagorasa w ΔABD
a
2=b
2+4e
2
a=
√6e=
√2*
√3e ⇒ a=
√3 b
|AB|=
√3|AD|
==========

9 mar 23:34
mydlix: Mnie w szkole uczą pisać: c.k.d. − co kończy dowód.
Ale chyba najważniejsze, żeby był on poprawny, a nie jakim skrótem go zakończymy.
9 mar 23:49
ello:
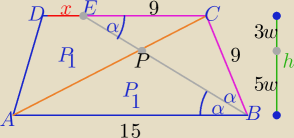
1/ ΔBCF równoramienny |EC|=|BC|=9
| | 15 | | 5 | |
2/ ΔABP ∼ΔECP (kkk) w skali k= |
| = |
| |
| | 9 | | 3 | |
| | x+15 | | 1 | |
P(ABED)= |
| *8w =2P1 P(APB)= |
| *15*5w |
| | 2 | | 2 | |
.......................
x+15=75/4
x=..........
10 mar 00:01
Damian#UDM: ello to zadanie już było robione, chodziło tylko o iloczyny. Lecz dziękuję za Twoją pracę

Pozdrawiam
10 mar 01:32
getin:
Bardziej na konkurs niż na maturę, ale spróbujcie:
Dla każdego naturalnego n≥1 dany jest ciąg
an = 20212021n+20212021+20212022a20212020
Oblicz a20212021
10 mar 07:28
ite:
getin czy odpowiedź to 0 ?
10 mar 21:57
getin:
Tak, wynik to zero
Wynik do tego zadania jest liczbą która pokazuje, ile warte jest zdalne nauczanie
10 mar 22:02
Mila:
Kogo obwiniasz getin ?
10 mar 22:25
ite: Za surowo oceniasz. Naprawdę wysiłek tych, którzy prowadzą zdalne i tych, którzy pomimo
trudności uczą się w taki sposób, ma niezerową wartość.
10 mar 22:26
Saizou :
Niech p = 20212021, wówczas
an = pn + p + (p+1)ap−1
dla n = p−1 mamy
ap−1 = p(p−1) +p+(p+1)ap−1 → ap−1 = −p
dla n = p mamy
ap = p2 + p + (p+1)(−p) = 0
a20212021 = 0
10 mar 22:26
Goblin: Kiedy ktoś sądzi że jest lepszy od innych ,
Uśmiechnij się tylko i nie psuj marzeń temu pierwszemu

10 mar 22:42
getin:
dla jasności, w żadnym wypadku nie winię nauczycieli bo oni są Bogu ducha winni,
winię tych, którzy przyczynili się swoimi decyzjami do wprowadzenia pomysłu zamknięcia szkół
10 mar 23:06
Qulka: przez lata wszyscy moi maturzyści marzyli jak im byłoby lepiej gdyby nie musieli biegać do
szkoły...
..
Rozporządzenie MEN z 2017r.: (jeszcze nie było mowy o pandemii)
uczeń ma :
myśleć, czytać, komunikować się , kreatywnie rozwiązywać problemy,
posługiwać się TIK, samodzielnie docierać do informacji, być systematyczny
pracować w grupie
zamknięcie szkół temu nie przeszkadza a nawet bardzo pomaga...
świat się zmienia coraz szybciej.. pokolenia się zmieniają coraz szybciej..
nie oceniajmy przez swój pryzmat co jest potrzebne i dobre obecnie...
bo naprawdę nie wiemy co będzie potrzebne za chwilę ...
i tak to co nam się wydaje, że szkoła miała dać uczniom to już dawno przeżytek ..
10 mar 23:44
getin:
coś w tym jest...
na wyciszenie się i uspokojenie nastrojów podam zadanie... na dziś lub jutro, dla chętnej lub
chętnego
W urnie U jest 6 kulek: 2 białe i 4 czarne. Losujemy jedną kulę z tej urny.
O ile % wzrosłoby prawdopodobieństwo wylosowania czarnej kulki gdyby przed losowaniem dołożono
do tej urny U jeszcze dodatkowe 2 czarne kulki ?
10 mar 23:58
Qulka: o 12,5%
11 mar 00:05
getin:

To jeszcze takie.. może być trochę męczące i nużące no ale już późno jest i trzeba iść spać...
W trójkącie ABC o bokach |AB| = 7, |BC| = 5, |AC| = 3 i kącie ACB równym 120
o poprowadzono z
wierzchołka C:
− wysokość CK
− dwusieczną kąta ACB która przecięła bok AB w punkcie L
− środkową CM
a) oblicz |CK|
| | |LM| | |
b) oblicz stosunek długości |
| |
| | |MB| | |
11 mar 00:22
Qulka: a) 15√3/14 b)1/4
11 mar 00:53
getin:
Tak dokładnie wychodzi..
więc teraz takie:
W trójkącie ABC mamy |AB| = x, |BC| = 6, |AC| = 5. Odchylenie standardowe trzech liczb: |AB|,
Oblicz długość boku AB
11 mar 11:41
Saizou :
Warunki z nierówności trójkąta mamy
x+6>5 i x+5>6 i 5+6>x i x>0
x > −1 i x> 1 i 11>x i x>0 ⇒x ∊ (1, 11)
| | √42 | |
odchylenie standardowe: δ = |
| |
| | 3 | |
| | 42 | | 14 | |
wariancja: δ2 = |
| = |
| |
| | 9 | | 3 | |
| | x+5+6 | | x+11 | |
średnia arytmetyczna: d = |
| = |
| |
| | 3 | | 3 | |
| 14 | | | | x+11 | | x+11 | | x+11 | | (x− |
| )2 + (5− |
| )2 + (6 − |
| )2 | | | 3 | | 3 | | 3 | |
| |
| = |
| |
| 3 | | 3 | |
| | 2x−11 | | 4−x | | 7−x | |
14 = ( |
| )2 + ( |
| )2 + ( |
| )2 |
| | 3 | | 3 | | 3 | |
9*14 = (2x−11)
2 + (4−x)
2 + (7−x)
2
9*14 = 4x
2 − 44x +121 + 16 − 8x + x
2 +49 −14x + x
2
x = 1 ∉ (1,11) lub x = 10 ∊ (1,11)
|AB| = 10
11 mar 12:07
getin:

Teraz coś dla maniaków wielomianów i delty:
Wyznacz wszystkie wartości parametru m, dla których suma kwadratów różnych rozwiązań x
1, x
2
równania
x
2 + 2m*x + m
3+2 = 0
jest mniejsza od 28
11 mar 12:48
6latek:
1) Δ>0
4m
2−4m
3−8>0
−4m
3+4m
2−8>0
m
3−m
2+2<0
dla m=−1 m
3−m
2+2=0
(m
3−m
2+2)/(m+1)= m
2−2m+2
m
3−m
2+2=(m+1)(m
2−2m+2)<0 ⇔m+1<0 to m<−1 bo m
2−2m+2 stale dodatnie
Δ>0 dla m∊(−
∞,−1)
2)x
12+x
22<28
(−2m)
2−2(m
3+2)<28
4m
2−2m
3−4<28
−2m
3+4m
2−4<28/:(−2)
m
3−2m
2+2>−14
m
3−2m
2+16>0
dla m=±1≠0
dla m=2
8−8+16≠0
dla m=−2
−8−8+16=0
(m
3−2m
2+16)/(m+2)=m
2−4m+8
m
3−2m
2+16=(m+2)(m
2−4m+8)>0 ⇔m+2>0 to m>−2 bo m
2−4m+8 jest stale dodatnie
x
12+x
22<28 dla m∊(−2,
∞)
Dla m∊(−2,−1) suma kwadratow pierwiastkow roznych tego rownania jest mniejsza od 28 .
11 mar 20:39
Damian#UDM:
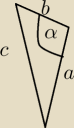 https://drive.google.com/drive/folders/1fdnA_CwbjFnIKn4mlfMLwjAhmIKhwbQ8?usp=sharing
https://drive.google.com/drive/folders/1fdnA_CwbjFnIKn4mlfMLwjAhmIKhwbQ8?usp=sharing
dowód geometryczny (0 − 3) PR ZI 2021 III
Na bokach trójkąta zbudowano kwadraty o polach P1, P2 i P3 (zobacz rysunek)
Wykaż, że
Czy można to zadanie wykazać za pomocą twierdzenia Pitagorasa?
dla 90<α<180 stopni
a
2 + b
2 < c
2 , lecz a
2 + b
2 >
12c
2
dla 0<α<90 stopni
a
2 + b
2 > c
2 oraz a
2 + b
2 >
12c
2
dla α=90 stopni
a
2 + b
2 = c
2 oraz a
2 + b
2 >
12c
2
Czy takie rozumowanie jest poprawnie przeprowadzone?
20 mar 18:23
ICSP: jakie "rozumowanie" ?
Tutaj nie ma żadnego rozumowania.
20 mar 18:43
Damian#UDM: a czy może być takie rozwiązanie tego zadania?
20 mar 19:30
Minato:
Nie może, bo nic nie dowiodłeś.
20 mar 19:57
Minato:
P
1 = a
2
P
2 = b
2
P
3 = c
2, wówczas mamy do udowodnienia nierówność równoważną:
Z nierówności trójkąta
a + b > c
Z nierówności między średnimi
20 mar 20:12
Qba:
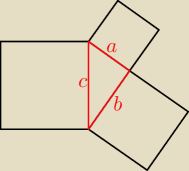
Pola kwadratów: P
1 = a
2, P
2 = b
2, P
3 = c
2.
Z nierówności trójkąta:
a + b > c obustronnie do kwadratu: a
2 + b
2 + 2ab > c
2
oczywista nierówność: (a − b)
2 ≥ 0 stąd a
2 + b
2 − 2ab ≥ 0
+ −−−−−−−−−−−−−−−
2a
2 + 2b
2 > c
2
| | 1 | | 1 | |
zatem a2 + b2 > |
| c2, wobec tego P1 + P2 > |
| P3 |
| | 2 | | 2 | |
20 mar 20:16
Damian#UDM: Bardzo dziękuję wam za pomoc

20 mar 23:02
Damian#UDM: https://drive.google.com/drive/u/0/folders/1fdnA_CwbjFnIKn4mlfMLwjAhmIKhwbQ8
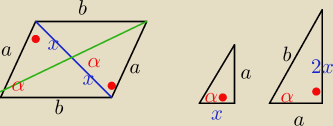
12. (0 − 5) dowód geometryczny ZI 2021 PR
Na bokach trójkąta ABC zbudowano kwadraty ABKL, BCMN i CAOP (zobacz rysunek).
Kąty BAC i ABC są ostre oraz suma ich tangensów jest równa
32. Wykaż, że jeżeli pole
kwadratu ABKL jest trzy razy większe od pola trójkąta ABC, to suma pól kwadratów BCMN i
CAOP tez jest trzy razy większa od pola trójkąta ABC.
21 mar 15:38
Qba:
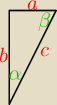
| | 1 | | k | |
Pole trójkąta prostokątnego P = |
| ab. Jeśli tgα + tgβ = |
| , k>0 |
| | 2 | | 2 | |
| a | | b | | k | | 1 | |
| + |
| = |
| /*ab, a2 + b2 = k* |
| ab = kP = c2. |
| b | | a | | 2 | | 2 | |
W tym przykładzie k = 3
21 mar 18:12
Oba:

....
Qba 
21 mar 18:34
Qba:


21 mar 19:21
Oba:

21 mar 19:24
pawik:
21 mar 19:25
Damian#UDM: Tylko my nie wiemy czy to jest trójkąt prostokątny. Więc można tak zadanie rozwiązać?
21 mar 19:28
ICSP: | | 3 | | c2 | |
Wiemy, że tgα + tgβ = |
| oraz, że PΔ = |
| i mamy pokazać, że ten trójkąt jest |
| | 2 | | 3 | |
prostokątny.
Z twierdzenia sinusów:
| | a | | b | |
sin(α + β) = |
| = |
| |
| | csinα | | csinβ | |
| | 1 | | sinαsinβc2 | | c2 | |
P = |
| absin(α+β) = |
| = |
| |
| | 2 | | 2sin(α+β) | | 3 | |
Stąd
| | 3 | |
Z warunku tgα + tgβ = |
| dostajemy |
| | 2 | |
| | 3 | |
sin(α + β) = |
| cosαcosβ |
| | 2 | |
Dlatego mamy
| | 2 | | 2 | | 3 | |
sinαsinβ = |
| sin(α + β) = |
| * |
| cosαcosβ |
| | 3 | | 3 | | 2 | |
cos(α + β) = 1
I to jest nasza teza.
21 mar 21:08
ICSP: Eta przyjdzie to poda łatwiejszy sposób.
21 mar 21:09
ICSP: Powinno być:
cos(α + β) = 0
21 mar 21:15
Saizou :
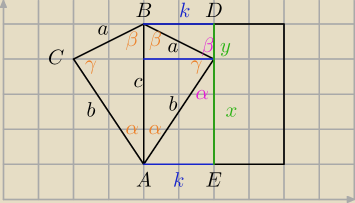
Alternatywny dowód:
| 3 | | k | | k | | x+y | | kc | |
| = |
| + |
| = k( |
| ) = |
| |
| 2 | | x | | y | | xy | | xy | |
3xy = 2kc
−−−−−−−−−−−
P − pole trójkąta ABC, zatem pole ABED jest równe
−−−−−−−−−−−
−−−−−−−−−−−
Z treści zadania
c
2 = 3P
−−−−−−−−−−−
Z tw. Pitagorasa
b
2 = k
2 + x
2
a
2 = k
2 + y
2
================+
a
2+b
2 = 2k
2 +x
2+y
2 = 2k
2+(x+y)
2−2xy =
| | 4 | | 4 | | 17 | | 8 | | 17−8 | |
= 2* |
| c2 + c2 − 2* |
| P = |
| *3P − |
| P = |
| P = 3P |
| | 9 | | 3 | | 9 | | 3 | | 3 | |
a
2+b
2=3P
co należało pokazać
21 mar 21:42
Eta:

Ze wzoru na pole dowolnego trójkąta
| | 1 | c2 | | 3 | |
P= |
|
| i tgα+tgβ= |
| |
| | 2 | ctgα+ctgβ) | | 2 | |
zatem tgα*tgβ=1
sinα*sinβ−cosα*cosβ=0
cos(α+β)=0
α+β=90
o = γ
ΔABC prostokątny
i dalej jak podał
Qba
21 mar 21:53
21 mar 21:54
ICSP: Właśnie wystarczyło pokazać, że trójkąt jest prostokątny

Teza to tak naprawdę twierdzenie Pitagorasa.
21 mar 21:56
Qba:
Liczbę 3 można tu zamienić na inną liczbę
21 mar 23:14
Damian#UDM: 14. (0 − 5) PR ZI 2021 IV
Zadanie z równoległobokiem w układzie współrzędnych z parametrem.
Wyszły mi ogromne pierwiastki, więc proszę o pomoc

22 mar 04:44
chichi:
| | 1 | |
W parę sekund dochodzimy do równania postaci |m(m−2)|= |
| , rozwiąż je  |
| | 3 | |
22 mar 08:48
Damian#UDM: | | √10 | |
Tylko iloczyn tych wysokości jest równy |
| więc nie wiem skąd wzięła się 13  |
| | 15 | |
22 mar 13:20
Damian#UDM: Dziękuję
Eta ,
ICSP ,
Saizou oraz
Qba za rozwiązanie wcześniejszego zadania

22 mar 13:22
22 mar 13:43
chichi:
Stąd:

| |−2m−(−m)| | | |1−(−m+3)| | | √10 | |
| * |
| = |
| |
| √14+1 | | √1+1 | | 15 | |
30|m(m−2)|=10
22 mar 13:56
Damian#UDM: No tak, przyjąłem sobie, że sytuacja jest podobna, gdy równoległobok byłby równoległy do osi
O
x, a przecież tak nie jest. Dziękuję za rozjaśnienie

22 mar 20:10
Damian#UDM:
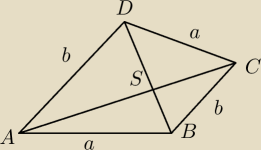
6. (0−3) ZI 2021 PR V
Przekątne czworokąta wypukłego ABCD dzielą go na cztery trójkąty. Wykaż, że jeżeli
promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt ABCD
można wpisać okrąg.
Skorzystałem z twierdzenia sinusów w każdym trójkącie i wyszło mi, że
|AB|=|CD|=a oraz |BC|=|AD|=b
|∡ASB|=|∡CSD|=α oraz |∡ASD|=|∡BSC|=β
Zatem otrzymałem równoległobok. Żeby wykazać, że w czworokąt ABCD można wpisać okrąg to mu
zajść warunek
a + a=b + b
A jak do tego dojść to już nie wiem

Proszę o pomoc.
7. (0−3) ZI 2021 PR V
Liczby rzeczywiste a, b spełniają warunek
a
3+3a
2+3a=8b
3+12b
2+6b. Wykaż, że a=2b
Po przekształceniach otrzymałem
(a−2b)*[(a+1)
2+(a+1)*(2b+1)+(2b+1)
2]=0
a−2b=0⇔a=2b, czyli otrzymałem pożądany warunek, a z drugiego równania
[(a+1)
2+(a+1)*(2b+1)+(2b+1)
2]=0
dla a=−1 oraz b=−
12
zachodzi równość
0=0
i zauważyłem, że −1=2*(−
12) , czyli a=2b
Czy zadanie zostało poprawnie rozwiązane ?

9. (0−3) ZI 2021 PR V
Dany jest trapez ABCD o podstawach AB i CD, w którym |BC| = 5
√2. Okrąg opisany na
trójkącie ABD przecina prostą CD w takim punkcie E, że |AE| = 10 i |∡AED| = 45◦. Oblicz
długość podstawy CD trapezu ABCD.
Tutaj dzięki kątom wpisanym i środkowym, zauważyłem kąty proste i wyszło mi, że promień okręgu
opisanego na trójkącie ABD jest równy 5.
Lecz również otrzymałem sprzeczność, gdyż otrzymałem, że |BE|=|BC|=5
√2, a trójkąt BEC jest
prostokątny.
Więc proszę o pomoc

31 mar 11:20
chichi:
a
3+3a
2+3a=8b
2+12b
2+6b / +1
a
3+3a
2+3a+1=8b
2+12b
2+6b+1
(a+1)
3=(2b+1)
3
a+1=2b+1
a=2b
Q.E.D.
Zerknę na resztę po zajęciach

31 mar 11:34
Damian#UDM: No tak, można było od razu spierwiastkować, zamiast rozpisywać ze wzoru a
−b
3.
Dziękuję za uwagę

31 mar 11:37
Damian#UDM: Rozpisywać ze wzoru a3−b3
31 mar 11:37
Saizou :
 Damian
Damian załóż nowy post, bo tutaj już się tasiemiec robi.
Z kątów opartych na tym samym łuku
<ABD = < AED = α = 45
Trapez ABED jest wpisany w okrąg, zatem jest to trapez równoramienny.
Trójką AFE to trójkąt 'ekierokowy' → AF = FE = 5
√2
Skoro AF = BC → BC jest wysokością trapezu.
Trójkąt BDC jest trójkątem ekierkowym, zatem CD=BC = 5
√2
31 mar 12:28
Saizou :
β = 180−α
sinβ = sin(180−α)=sinα
Z tw. sinusów
| AB | |
| = 2R → AB = 2Rsinα |
| sinα | |
| DC | |
| = 2R → DC = 2Rsinα |
| sinα | |
| BC | |
| = 2R → BC = 2Rsinα |
| sinβ | |
| AD | |
| = 2R → AD = 2Rsinα |
| sinα | |
WNIOSEK:
ABCD jest rombem, zatem można opisać na czworokącie ABCD okrąg
31 mar 16:27
Damian#UDM: To ostatnie rozwiązane zadanie już wiem. Zamiast β to mogłem zapisać 180−α i ze wzoru
redukcyjnego na sinus
sin(180−α)=sin(α)
Sam sobie roboty i problemów robię

Dziękuje wam za pomoc!
31 mar 18:50
Saizou :
Na zdrowie

31 mar 20:39
Damian#UDM: Zastanawiam się nad jedną rzeczą, a mianowicie
jaka jest dziedzina funkcji
f(x)=logx2 ?
To jest to samo co 2logx
Czy dziedzina dla obu wyrażeń to x>0 ?
1 kwi 01:11
Qulka: takie działanie można zrobić tylko dla x>0
1 kwi 01:22
Damian#UDM: A jak nie muszę tego działania wykonywać to wtedy mam R/{0} ?
1 kwi 01:37
Damian#UDM: 13. (0−5) PR ZI 2021
Punkt S jest punktem przecięcia się środkowych trójkąta równoramiennego ABC o podstawie AB.
Okrąg o średnicy AB ma równanie
x
2+y
2+12x−10y+44=0, a cięciwa tego
okręgu równoległa do prostej AB i przechodząca przez punkt S zawiera się w prostej o równaniu x
− y + 14 = 0. Wyznacz równanie okręgu o środku C, który przechodzi przez punkty
A i B.
Równanie pierwszego okręgu
(x+6)
2+(y−5)
2=
√17
a dalej musiałem gdzieś zrobić błędy, proszę o pomoc

1 kwi 02:11
ICSP: f(x) = log(x2) , D : x ∊ R \{0}
f(x) = 2log|x|
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
g(x) = 2log(x) , D : x > 0
g(x) = log(x2)
1 kwi 08:37
Damian#UDM: Wszystko rozumiem, dziękuję

1 kwi 10:24
Saizou :
Damian załóż nowy post, bo ten już robi się tasiemcowaty

1 kwi 10:33
Qulka: skąd wytrzasnąłeś takie brzydkie cyferki że wszystko jest z pierwiastkami

Równanie pierwszego okręgu
(x+6)
2+(y−5)
2=
17
S(−15/2 ; 13/2 )
A(−6−
√17/2;5−
√17/2) B(−6+
√17/2;5+
√17/2)
C(−21/2 ; 19/2)
r drugiego =AC policz sobie
1 kwi 11:01
Damian#UDM: Saizou oczywiście tak zrobię
 Qulka
Qulka mój błąd. promień w równaniu miał być bez pierwiastka. Taki sam błąd zrobiłem na
maturze w maju 2017 roku w 13. zadaniu za 5 punktów. W odpowiedzi w równaniu okręgu zamiast
r
2 to dałem samo r − no i już punkty lecą. Niestety.
Punkty A i B wyszły mi takie same. Tylko nie mogę znaleźć kartki, gdzie to zadanie
rozwiązywałem.
Zrobię jeszcze raz i spytam się was gdzie jest moje błędne myślenie

1 kwi 13:27
Qulka: to jak chcesz robić jeszcze raz od początku to zrób takie
Punkt S jest punktem przecięcia się środkowych trójkąta równoramiennego ABC o podstawie AB.
Okrąg o średnicy AB ma równanie x2+y2+12x−10y+
43=0, a cięciwa tego
okręgu równoległa do prostej AB i przechodząca przez punkt S zawiera się w prostej o równaniu x
− y +
15 = 0. Wyznacz równanie okręgu o środku C, który przechodzi przez punkty A i B.
chyba się wtedy zrobi równiej

1 kwi 14:07
Damian#UDM: Dobra, mam.
Punkt O jest środkiem odcinka AB i ma współrzędne (−6,5), promień tego okręgu to r=
√17.
Na prostej k:y=x+14 leży punkt S=(x,x+14) − w sumie nie wiem po co ten punkt jest podany

Prosta, prostopadła do odcinka AB ma równanie y=−x−1, czyli punkt C ma współrzędne C=(x,−x−1)
i teraz współrzędne punktu C mogę policzyć z równania.... i tego właśnie nie wiem

Ale chyba już wiem − po to jest ten punkt podany, bo wtedy wysokość dzieli się w stosunku 2:1
A długość odcinka SO to 3, więc CS to 6

i z tego równania powinny wyjść współrzędne,
zobaczymy.
1 kwi 14:14
Damian#UDM: S mi wyszedł (−7,5;6,5)
i wtedy |SO|=3, czyli |CS|=6
i z tego równania wychodzi mi
(x+
152)
2=18
więc chyba niestety coś źle

1 kwi 14:17
Damian#UDM: | | 3√2 | |
|SO|= |
| , czyli jednak nie mogę tego odczytać z odległości między prostymi |
| | 2 | |
y=x+11 oraz y=x+14, no trudno

1 kwi 14:20
Qulka: możesz ..odległość między równoległymi prostymi (tylko zapisanymi w postaci ogólnej) to
1 kwi 14:28
Qulka: czyli u Ciebie 3/√2
1 kwi 14:28
Qulka: i tak..CS=2SO więc masz C i potem CA to r
1 kwi 14:30
Damian#UDM: Równanie okręgu wyszło mi
(x+212)2+(y−192)2=1152
1 kwi 14:31
Qulka: i C leży na prostopadłej do AB przez O
1 kwi 14:31
Damian#UDM: Myślę, że jest ok

Super, dziękuję
Qulka za ten wzór, bo ja po prostu odejmowałem współczynniki b, tak jak w
przypadku prostych na przykład y=7 orz y=4, ale teraz widzę, że to tak nie działa

Zapisuje sobie ten wzór

1 kwi 14:32


 Przy okazji witam
Przy okazji witam 



 dziekuje za wyjasnienie .
Tak naprawde to znam tylko rosyjski . Uczyli tylko wtedy tego języka .
dziekuje za wyjasnienie .
Tak naprawde to znam tylko rosyjski . Uczyli tylko wtedy tego języka .




 kiedyś też używaliśmy c.b.d.o lub c.b.d.u
"co było do okazania" , "co było do udowodnienia"
kiedyś też używaliśmy c.b.d.o lub c.b.d.u
"co było do okazania" , "co było do udowodnienia"




 Wyżej 25 lut 19:38 zakładam, że z nierówności trójkąta tak jak Eta napisała
a < b + c ⇔ a2 < (b+c)2
i to jest na pewno prawdziwe, więc pytam się czy jeśli wiem, że nierówność wyżej jest prawdziwa
to czy w nierówności
a2 + b2 + c2 < (b+c)2 + (b+c)2 pokaże, że b2 + c2 < (b+c)2 jest też prawdziwe to czy
zadanie będzie prawidłowo wykonane?
A rozwiązanie b2 + c2 < (b+c)2 przedstawiłem w 25 lut 19:38
Wyżej 25 lut 19:38 zakładam, że z nierówności trójkąta tak jak Eta napisała
a < b + c ⇔ a2 < (b+c)2
i to jest na pewno prawdziwe, więc pytam się czy jeśli wiem, że nierówność wyżej jest prawdziwa
to czy w nierówności
a2 + b2 + c2 < (b+c)2 + (b+c)2 pokaże, że b2 + c2 < (b+c)2 jest też prawdziwe to czy
zadanie będzie prawidłowo wykonane?
A rozwiązanie b2 + c2 < (b+c)2 przedstawiłem w 25 lut 19:38



 kochana jesteś! Pozdrawiam serdecznie
kochana jesteś! Pozdrawiam serdecznie 


 1/ z własności dwusiecznej ΔBCE równoramienny
to |EC|=|BC|=9
2/ Z podobieństwa ΔABP i EPC (z cechy (kkk)
1/ z własności dwusiecznej ΔBCE równoramienny
to |EC|=|BC|=9
2/ Z podobieństwa ΔABP i EPC (z cechy (kkk)




 7. (0−3)
https://drive.google.com/drive/folders/1UyCWF8p4RFQF-6j-bJ10ZtIlqZVR2G-A?usp=sharing
Przekątne AC i BD równoległoboku ABCD przecinają się w punkcie S. Przekątna BD jest
prostopadła do boków AD i BC, a |∡BAD| = |∡BSC| (zob. rysunek).
Udowodnij, że |AB| = |AD|*√3.
W tym zadaniu znalazłem trójkąty podobne oraz wyznaczyłem wszystkie kąty, lecz nie mam pomysłu
jak dojść do podanej tezy.
Zadanie 15. (0−7) (treść zadania na dysku w linku wyżej)
b) Wyznacz dziedzinę funkcji f.
c) Wyznacz współrzędne takiego punktu P, dla którego funkcja f osiąga wartość najmniejszą
Zastanawiam się jak wyznaczyć dziedzinę funkcji f. Punkt ma leżeć wewnątrz kąta. Narysowałem
sobie podaną sytuację.
Czy to oznacza, że x ∊ (1,3) ? Szczerze mówiąc nie mam pomysłu jak to algebraicznie wyznaczyć.
Proszę o wskazówki oraz pomoc
7. (0−3)
https://drive.google.com/drive/folders/1UyCWF8p4RFQF-6j-bJ10ZtIlqZVR2G-A?usp=sharing
Przekątne AC i BD równoległoboku ABCD przecinają się w punkcie S. Przekątna BD jest
prostopadła do boków AD i BC, a |∡BAD| = |∡BSC| (zob. rysunek).
Udowodnij, że |AB| = |AD|*√3.
W tym zadaniu znalazłem trójkąty podobne oraz wyznaczyłem wszystkie kąty, lecz nie mam pomysłu
jak dojść do podanej tezy.
Zadanie 15. (0−7) (treść zadania na dysku w linku wyżej)
b) Wyznacz dziedzinę funkcji f.
c) Wyznacz współrzędne takiego punktu P, dla którego funkcja f osiąga wartość najmniejszą
Zastanawiam się jak wyznaczyć dziedzinę funkcji f. Punkt ma leżeć wewnątrz kąta. Narysowałem
sobie podaną sytuację.
Czy to oznacza, że x ∊ (1,3) ? Szczerze mówiąc nie mam pomysłu jak to algebraicznie wyznaczyć.
Proszę o wskazówki oraz pomoc 
 ∡ASD = α
ΔABD ~ΔSAD (kkk)
∡ASD = α
ΔABD ~ΔSAD (kkk)
 zadanie 7
zadanie 7
 Oraz ICSP za
cenną wskazówkę
Oraz ICSP za
cenną wskazówkę 
 Szukałem miejsc zerowych tego równania lecz nie mogę znaleźć.
Proszę o pomoc
Szukałem miejsc zerowych tego równania lecz nie mogę znaleźć.
Proszę o pomoc 
 x3 + 5x2 + mx + m − 4 = x3 + x2 + m(x + 1) + 4x2 − 4 = x2(x + 1) + m(x + 1) + 4(x2 − 1)
= x2(x + 1) + m(x + 1) + 4(x − 1)(x + 1) =
= (x + 1)(x2 + m + 4(x − 1)) = (x + 1)(x2 + m + 4x − 4) =
= (x + 1)(x2 + 4x + m − 4)
Teraz lepiej?
x3 + 5x2 + mx + m − 4 = x3 + x2 + m(x + 1) + 4x2 − 4 = x2(x + 1) + m(x + 1) + 4(x2 − 1)
= x2(x + 1) + m(x + 1) + 4(x − 1)(x + 1) =
= (x + 1)(x2 + m + 4(x − 1)) = (x + 1)(x2 + m + 4x − 4) =
= (x + 1)(x2 + 4x + m − 4)
Teraz lepiej?


 chyba jeszcze przyda się warunek x2≠−1 oraz x3≠−1
chyba jeszcze przyda się warunek x2≠−1 oraz x3≠−1 





 "ciąg dalszy nastąpi "
"ciąg dalszy nastąpi "
 Jestem w szoku, chciałbym widzieć tak szybko rozwiązania i pomysły jak wy
Jestem w szoku, chciałbym widzieć tak szybko rozwiązania i pomysły jak wy  Pozdrawiam was kochani!
Pozdrawiam was kochani!

 W pierwszy zsumowałem najpierw cos(α) oraz cos(5α) no i dlatego nie wyszło mi
W pierwszy zsumowałem najpierw cos(α) oraz cos(5α) no i dlatego nie wyszło mi  A na drugie aż tak daleko na ten pomysł nie wpadłem. Dziękuję wam za pomoc
A na drugie aż tak daleko na ten pomysł nie wpadłem. Dziękuję wam za pomoc 



 zad 7/
ΔABD ∼BCS z cechy (kkk)
zad 7/
ΔABD ∼BCS z cechy (kkk)

 1/ ΔBCF równoramienny |EC|=|BC|=9
1/ ΔBCF równoramienny |EC|=|BC|=9
 Pozdrawiam
Pozdrawiam

 To jeszcze takie.. może być trochę męczące i nużące no ale już późno jest i trzeba iść spać...
W trójkącie ABC o bokach |AB| = 7, |BC| = 5, |AC| = 3 i kącie ACB równym 120o poprowadzono z
wierzchołka C:
− wysokość CK
− dwusieczną kąta ACB która przecięła bok AB w punkcie L
− środkową CM
a) oblicz |CK|
To jeszcze takie.. może być trochę męczące i nużące no ale już późno jest i trzeba iść spać...
W trójkącie ABC o bokach |AB| = 7, |BC| = 5, |AC| = 3 i kącie ACB równym 120o poprowadzono z
wierzchołka C:
− wysokość CK
− dwusieczną kąta ACB która przecięła bok AB w punkcie L
− środkową CM
a) oblicz |CK|
 Teraz coś dla maniaków wielomianów i delty:
Wyznacz wszystkie wartości parametru m, dla których suma kwadratów różnych rozwiązań x1, x2
równania
x2 + 2m*x + m3+2 = 0
jest mniejsza od 28
Teraz coś dla maniaków wielomianów i delty:
Wyznacz wszystkie wartości parametru m, dla których suma kwadratów różnych rozwiązań x1, x2
równania
x2 + 2m*x + m3+2 = 0
jest mniejsza od 28
 1) Δ>0
4m2−4m3−8>0
−4m3+4m2−8>0
m3−m2+2<0
dla m=−1 m3−m2+2=0
(m3−m2+2)/(m+1)= m2−2m+2
m3−m2+2=(m+1)(m2−2m+2)<0 ⇔m+1<0 to m<−1 bo m2−2m+2 stale dodatnie
Δ>0 dla m∊(−∞,−1)
2)x12+x22<28
(−2m)2−2(m3+2)<28
4m2−2m3−4<28
−2m3+4m2−4<28/:(−2)
m3−2m2+2>−14
m3−2m2+16>0
dla m=±1≠0
dla m=2
8−8+16≠0
dla m=−2
−8−8+16=0
(m3−2m2+16)/(m+2)=m2−4m+8
m3−2m2+16=(m+2)(m2−4m+8)>0 ⇔m+2>0 to m>−2 bo m2−4m+8 jest stale dodatnie
x12+x22<28 dla m∊(−2,∞)
Dla m∊(−2,−1) suma kwadratow pierwiastkow roznych tego rownania jest mniejsza od 28 .
1) Δ>0
4m2−4m3−8>0
−4m3+4m2−8>0
m3−m2+2<0
dla m=−1 m3−m2+2=0
(m3−m2+2)/(m+1)= m2−2m+2
m3−m2+2=(m+1)(m2−2m+2)<0 ⇔m+1<0 to m<−1 bo m2−2m+2 stale dodatnie
Δ>0 dla m∊(−∞,−1)
2)x12+x22<28
(−2m)2−2(m3+2)<28
4m2−2m3−4<28
−2m3+4m2−4<28/:(−2)
m3−2m2+2>−14
m3−2m2+16>0
dla m=±1≠0
dla m=2
8−8+16≠0
dla m=−2
−8−8+16=0
(m3−2m2+16)/(m+2)=m2−4m+8
m3−2m2+16=(m+2)(m2−4m+8)>0 ⇔m+2>0 to m>−2 bo m2−4m+8 jest stale dodatnie
x12+x22<28 dla m∊(−2,∞)
Dla m∊(−2,−1) suma kwadratow pierwiastkow roznych tego rownania jest mniejsza od 28 .
 https://drive.google.com/drive/folders/1fdnA_CwbjFnIKn4mlfMLwjAhmIKhwbQ8?usp=sharing
dowód geometryczny (0 − 3) PR ZI 2021 III
Na bokach trójkąta zbudowano kwadraty o polach P1, P2 i P3 (zobacz rysunek)
Wykaż, że
https://drive.google.com/drive/folders/1fdnA_CwbjFnIKn4mlfMLwjAhmIKhwbQ8?usp=sharing
dowód geometryczny (0 − 3) PR ZI 2021 III
Na bokach trójkąta zbudowano kwadraty o polach P1, P2 i P3 (zobacz rysunek)
Wykaż, że
 Pola kwadratów: P1 = a2, P2 = b2, P3 = c2.
Z nierówności trójkąta:
a + b > c obustronnie do kwadratu: a2 + b2 + 2ab > c2
oczywista nierówność: (a − b)2 ≥ 0 stąd a2 + b2 − 2ab ≥ 0
+ −−−−−−−−−−−−−−−
2a2 + 2b2 > c2
Pola kwadratów: P1 = a2, P2 = b2, P3 = c2.
Z nierówności trójkąta:
a + b > c obustronnie do kwadratu: a2 + b2 + 2ab > c2
oczywista nierówność: (a − b)2 ≥ 0 stąd a2 + b2 − 2ab ≥ 0
+ −−−−−−−−−−−−−−−
2a2 + 2b2 > c2


 .... Qba
.... Qba 



 Alternatywny dowód:
Alternatywny dowód:
 Ze wzoru na pole dowolnego trójkąta
Ze wzoru na pole dowolnego trójkąta
 Teza to tak naprawdę twierdzenie Pitagorasa.
Teza to tak naprawdę twierdzenie Pitagorasa.







 6. (0−3) ZI 2021 PR V
Przekątne czworokąta wypukłego ABCD dzielą go na cztery trójkąty. Wykaż, że jeżeli
promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt ABCD
można wpisać okrąg.
Skorzystałem z twierdzenia sinusów w każdym trójkącie i wyszło mi, że
|AB|=|CD|=a oraz |BC|=|AD|=b
|∡ASB|=|∡CSD|=α oraz |∡ASD|=|∡BSC|=β
Zatem otrzymałem równoległobok. Żeby wykazać, że w czworokąt ABCD można wpisać okrąg to mu
zajść warunek
a + a=b + b
A jak do tego dojść to już nie wiem
6. (0−3) ZI 2021 PR V
Przekątne czworokąta wypukłego ABCD dzielą go na cztery trójkąty. Wykaż, że jeżeli
promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt ABCD
można wpisać okrąg.
Skorzystałem z twierdzenia sinusów w każdym trójkącie i wyszło mi, że
|AB|=|CD|=a oraz |BC|=|AD|=b
|∡ASB|=|∡CSD|=α oraz |∡ASD|=|∡BSC|=β
Zatem otrzymałem równoległobok. Żeby wykazać, że w czworokąt ABCD można wpisać okrąg to mu
zajść warunek
a + a=b + b
A jak do tego dojść to już nie wiem  Proszę o pomoc.
7. (0−3) ZI 2021 PR V
Liczby rzeczywiste a, b spełniają warunek
a3+3a2+3a=8b3+12b2+6b. Wykaż, że a=2b
Po przekształceniach otrzymałem
(a−2b)*[(a+1)2+(a+1)*(2b+1)+(2b+1)2]=0
a−2b=0⇔a=2b, czyli otrzymałem pożądany warunek, a z drugiego równania
[(a+1)2+(a+1)*(2b+1)+(2b+1)2]=0
dla a=−1 oraz b=−12
zachodzi równość
0=0
i zauważyłem, że −1=2*(−12) , czyli a=2b
Czy zadanie zostało poprawnie rozwiązane ?
Proszę o pomoc.
7. (0−3) ZI 2021 PR V
Liczby rzeczywiste a, b spełniają warunek
a3+3a2+3a=8b3+12b2+6b. Wykaż, że a=2b
Po przekształceniach otrzymałem
(a−2b)*[(a+1)2+(a+1)*(2b+1)+(2b+1)2]=0
a−2b=0⇔a=2b, czyli otrzymałem pożądany warunek, a z drugiego równania
[(a+1)2+(a+1)*(2b+1)+(2b+1)2]=0
dla a=−1 oraz b=−12
zachodzi równość
0=0
i zauważyłem, że −1=2*(−12) , czyli a=2b
Czy zadanie zostało poprawnie rozwiązane ?  9. (0−3) ZI 2021 PR V
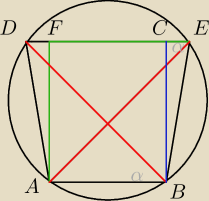
Dany jest trapez ABCD o podstawach AB i CD, w którym |BC| = 5√2. Okrąg opisany na
trójkącie ABD przecina prostą CD w takim punkcie E, że |AE| = 10 i |∡AED| = 45◦. Oblicz
długość podstawy CD trapezu ABCD.
Tutaj dzięki kątom wpisanym i środkowym, zauważyłem kąty proste i wyszło mi, że promień okręgu
opisanego na trójkącie ABD jest równy 5.
Lecz również otrzymałem sprzeczność, gdyż otrzymałem, że |BE|=|BC|=5√2, a trójkąt BEC jest
prostokątny.
Więc proszę o pomoc
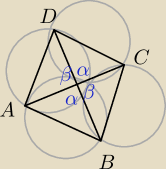
9. (0−3) ZI 2021 PR V
Dany jest trapez ABCD o podstawach AB i CD, w którym |BC| = 5√2. Okrąg opisany na
trójkącie ABD przecina prostą CD w takim punkcie E, że |AE| = 10 i |∡AED| = 45◦. Oblicz
długość podstawy CD trapezu ABCD.
Tutaj dzięki kątom wpisanym i środkowym, zauważyłem kąty proste i wyszło mi, że promień okręgu
opisanego na trójkącie ABD jest równy 5.
Lecz również otrzymałem sprzeczność, gdyż otrzymałem, że |BE|=|BC|=5√2, a trójkąt BEC jest
prostokątny.
Więc proszę o pomoc 


 Damian załóż nowy post, bo tutaj już się tasiemiec robi.
Z kątów opartych na tym samym łuku
<ABD = < AED = α = 45
Trapez ABED jest wpisany w okrąg, zatem jest to trapez równoramienny.
Trójką AFE to trójkąt 'ekierokowy' → AF = FE = 5√2
Skoro AF = BC → BC jest wysokością trapezu.
Trójkąt BDC jest trójkątem ekierkowym, zatem CD=BC = 5√2
Damian załóż nowy post, bo tutaj już się tasiemiec robi.
Z kątów opartych na tym samym łuku
<ABD = < AED = α = 45
Trapez ABED jest wpisany w okrąg, zatem jest to trapez równoramienny.
Trójką AFE to trójkąt 'ekierokowy' → AF = FE = 5√2
Skoro AF = BC → BC jest wysokością trapezu.
Trójkąt BDC jest trójkątem ekierkowym, zatem CD=BC = 5√2
 β = 180−α
sinβ = sin(180−α)=sinα
Z tw. sinusów
β = 180−α
sinβ = sin(180−α)=sinα
Z tw. sinusów
 Dziękuje wam za pomoc!
Dziękuje wam za pomoc!




 Równanie pierwszego okręgu
(x+6)2+(y−5)2=17
S(−15/2 ; 13/2 )
A(−6−√17/2;5−√17/2) B(−6+√17/2;5+√17/2)
C(−21/2 ; 19/2)
r drugiego =AC policz sobie
Równanie pierwszego okręgu
(x+6)2+(y−5)2=17
S(−15/2 ; 13/2 )
A(−6−√17/2;5−√17/2) B(−6+√17/2;5+√17/2)
C(−21/2 ; 19/2)
r drugiego =AC policz sobie
 Qulka mój błąd. promień w równaniu miał być bez pierwiastka. Taki sam błąd zrobiłem na
maturze w maju 2017 roku w 13. zadaniu za 5 punktów. W odpowiedzi w równaniu okręgu zamiast
r2 to dałem samo r − no i już punkty lecą. Niestety.
Punkty A i B wyszły mi takie same. Tylko nie mogę znaleźć kartki, gdzie to zadanie
rozwiązywałem.
Zrobię jeszcze raz i spytam się was gdzie jest moje błędne myślenie
Qulka mój błąd. promień w równaniu miał być bez pierwiastka. Taki sam błąd zrobiłem na
maturze w maju 2017 roku w 13. zadaniu za 5 punktów. W odpowiedzi w równaniu okręgu zamiast
r2 to dałem samo r − no i już punkty lecą. Niestety.
Punkty A i B wyszły mi takie same. Tylko nie mogę znaleźć kartki, gdzie to zadanie
rozwiązywałem.
Zrobię jeszcze raz i spytam się was gdzie jest moje błędne myślenie 

 Prosta, prostopadła do odcinka AB ma równanie y=−x−1, czyli punkt C ma współrzędne C=(x,−x−1)
i teraz współrzędne punktu C mogę policzyć z równania.... i tego właśnie nie wiem
Prosta, prostopadła do odcinka AB ma równanie y=−x−1, czyli punkt C ma współrzędne C=(x,−x−1)
i teraz współrzędne punktu C mogę policzyć z równania.... i tego właśnie nie wiem  Ale chyba już wiem − po to jest ten punkt podany, bo wtedy wysokość dzieli się w stosunku 2:1
A długość odcinka SO to 3, więc CS to 6
Ale chyba już wiem − po to jest ten punkt podany, bo wtedy wysokość dzieli się w stosunku 2:1
A długość odcinka SO to 3, więc CS to 6  i z tego równania powinny wyjść współrzędne,
zobaczymy.
i z tego równania powinny wyjść współrzędne,
zobaczymy.


 Super, dziękuję Qulka za ten wzór, bo ja po prostu odejmowałem współczynniki b, tak jak w
przypadku prostych na przykład y=7 orz y=4, ale teraz widzę, że to tak nie działa
Super, dziękuję Qulka za ten wzór, bo ja po prostu odejmowałem współczynniki b, tak jak w
przypadku prostych na przykład y=7 orz y=4, ale teraz widzę, że to tak nie działa  Zapisuje sobie ten wzór
Zapisuje sobie ten wzór 