 Oblicz pole trapezu:
a) równoramiennego, o ramieniu 25cm .Ponadto suma jego podstaw , które różnią się o 14
jest równa 34
b) prostokątnego o kącie ostrym 30, krótszej podstawie 2 i ramieniu dwa razy dłuższym od
krótszej podstawy
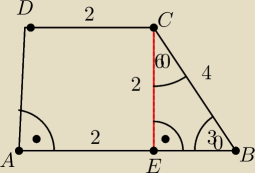
c) przedstawionego na rysunku dla a=2√3 i h= √3( rysunek jest u góry to pod punktu c))
lewy dolny kąt przy podstawie ma 45(stopni) prawy dolny kąt przy podstawie ma 60(stopni)
Oblicz pole trapezu:
a) równoramiennego, o ramieniu 25cm .Ponadto suma jego podstaw , które różnią się o 14
jest równa 34
b) prostokątnego o kącie ostrym 30, krótszej podstawie 2 i ramieniu dwa razy dłuższym od
krótszej podstawy
c) przedstawionego na rysunku dla a=2√3 i h= √3( rysunek jest u góry to pod punktu c))
lewy dolny kąt przy podstawie ma 45(stopni) prawy dolny kąt przy podstawie ma 60(stopni)
 W zwiazku z tym iz popelnilem blad przy liczeniu wysokosci tego trapezu
Wysokosc trapezu rownoramiennego bedzie srednia proporcjonalna miedzy bokami rownoleglymi kiedy
w ten trapez wpiszemy okrag (kolo )
Wtedy srednica kola ,okregu bedzie wysokoscia takiego trapezu
Jeszcze raz przepraszam i policze jak ma byc .
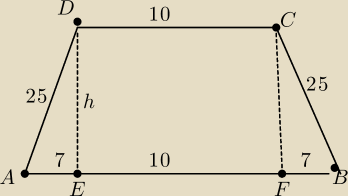
AE=FB=7 (to z obliczen
EF=DC=10
AD=BC=25
Rozpatrzy trojkat AED (prostokatny
stad
72+h2=252
49+h2=625
h2=625−49=576
h=√576=24
W zwiazku z tym iz popelnilem blad przy liczeniu wysokosci tego trapezu
Wysokosc trapezu rownoramiennego bedzie srednia proporcjonalna miedzy bokami rownoleglymi kiedy
w ten trapez wpiszemy okrag (kolo )
Wtedy srednica kola ,okregu bedzie wysokoscia takiego trapezu
Jeszcze raz przepraszam i policze jak ma byc .
AE=FB=7 (to z obliczen
EF=DC=10
AD=BC=25
Rozpatrzy trojkat AED (prostokatny
stad
72+h2=252
49+h2=625
h2=625−49=576
h=√576=24
| a+d | ||
P= | *h | |
| 2 |
| AB+CD | ||
P= | *CE | |
| 2 |
| 4√3 | ||
Z trojkata tego mamy EB= | = 2√3 | |
| 2 |
| 4 | ||
oraz CE=h= | =2 | |
| 2 |
| 2(1+√3 | ||
P= | *2= 2(1+√3)=2+2√3}j2 | |
| 2 |
| 1 | ||
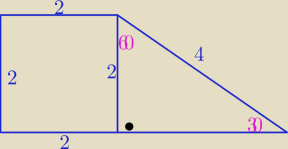
P=P□+P△ P□=22=4 , P△= | *2*4*sin60o = 2√3 | |
| 2 |
