Prawdopodobieństwo
Agaria208:
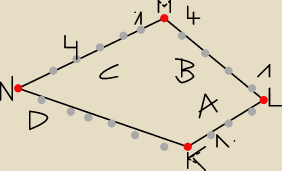
Dany jest czworokąt wypukły KLMN. Na jego boku KL zaznaczono trzy różne punkty (A
1, A
2, A
3),
na boku LM – cztery różne punkty (B
1, B
2, B
3, B
4), na boku MN – pięć różnych punktów
(C
1, C
2, C
3, C
4, C
5), a na boku KN – sześć różnych punktów (D
1, D
2, D
3, D
4, D
5,
D
6),jak na rysunku.
Spośród 22 punktów ze zbioru {K, L, M, N, A
1, A
2, A
3, B
1, B
2, B
3, B
4, C
1, C
2, C
3,
C
4, C
5, D
1, D
2, D
3, D
4, D
5, D
6} losujemy trzy.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane punkty będą
wierzchołkami pewnego trójkąta.
 Dany jest czworokąt wypukły KLMN. Na jego boku KL zaznaczono trzy różne punkty (A1, A2, A3),
na boku LM – cztery różne punkty (B1, B2, B3, B4), na boku MN – pięć różnych punktów
(C1, C2, C3, C4, C5), a na boku KN – sześć różnych punktów (D1, D2, D3, D4, D5,
D6),jak na rysunku.
Spośród 22 punktów ze zbioru {K, L, M, N, A1, A2, A3, B1, B2, B3, B4, C1, C2, C3,
C4, C5, D1, D2, D3, D4, D5, D6} losujemy trzy.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane punkty będą
wierzchołkami pewnego trójkąta.
Dany jest czworokąt wypukły KLMN. Na jego boku KL zaznaczono trzy różne punkty (A1, A2, A3),
na boku LM – cztery różne punkty (B1, B2, B3, B4), na boku MN – pięć różnych punktów
(C1, C2, C3, C4, C5), a na boku KN – sześć różnych punktów (D1, D2, D3, D4, D5,
D6),jak na rysunku.
Spośród 22 punktów ze zbioru {K, L, M, N, A1, A2, A3, B1, B2, B3, B4, C1, C2, C3,
C4, C5, D1, D2, D3, D4, D5, D6} losujemy trzy.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane punkty będą
wierzchołkami pewnego trójkąta.