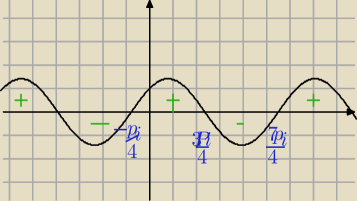
znak pochodnej jaros: Jak tutaj znaleźć znak pochodnej? c^x(sinx+cosx)

	3pi
miejsce zerowe to x =		+ kpi
	4

Qulka:

jaros: hmm no ale skąd mam wiedzieć jak to narysować?

jaros: Musze wyznaczyć monotoniczność i ekstrema i zaciąłem się ;x

Jerzy: Na początek podaj wzór funkcji a nie jakieś głupoty.

jaros: f(x0 = e^xsinx

jaros: f(x) = e^xsinx

ICSP: f(x) = e^xsinx

	π
f'(x) = ex(sinx + cosx) = √2exsin(x +		)
	4

jaros: @ICSP napisałbyś jakich operacji matematycznych użyłeś?

ICSP:

	π
możesz użyć wzoru na sumę sinusów ( cosx = sin(		− x))
	2

	√2
możesz użyć wzoru na sinus sumy kątów (wyciągasz √2 przed nawias i wyrażenia
	2

	π		π
zamieniasz na cos(		) i sin(		))
	4		4

Sposób dowolny.

Qulka: https://matematykaszkolna.pl/strona/3670.html

Mila:

√2
	*√2=1
2

	√2		√2
g(x)=√2*(		sinx +		cosx)=
	2		2

	π		π		π
=√2*(sinx*cos		+sin		*cosx)=√2*sin(x+		)
	4		4		4

jaros: Dobrze dziękuje wszystkim

jaros: Jeszcze jedno, cały czas uzyskuje wzór z sumy sinusów √2cos(x−π/4), wiedzą państwo, gdzie może być błąd? kalkulator pokazuje to samo Według wzoru powinno być √2cos(π/4−x).

asd: cos(−α)= cos(α)

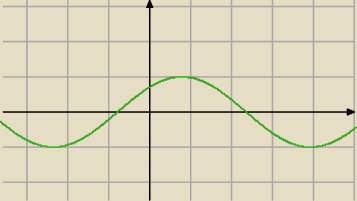
Mila:

	π
cos(x−π/4)=cos(π/4−x)=sin(x+		)
	4

cos(x−π/4)=cos(π/4−x) bo y=cosx jest funkcją parzystą

Marcysia: Dziękuję ślicznie

Qulka: https://matematykaszkolna.pl/forum/407050.html