zespolone Filip: Witam, jak rozwiazac rownanie z⁵=1, dziekuje z gory

ICSP: http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1111.pdf 10s szukania w googlach

6latek: Napisze je tak bo lepiej mi sie pisze u niz z u⁵=1 u⁵=0 (u−1)(u⁴+u³+u²+u+1)=0 stad u=1 lub u⁴+u³+u²+u+1=0 u=0 nie jest pierwiastkiem tego rownania wiec dzielimy obie strony tego rownania przez u² Mamy wtedy

	1		1
A)u2+u+1+		+		=0
	u		u2

Podstawienie

	1
t=u+
	u

−−−−−−−−−−−−−−−−

	1		1
stad t2= (u+		)2 = u2+2+
	u		u2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− z tego mamy

	1
u2+		= t2−2
	u2

Rownanie A zapiszmy tak

	1		1
(u2+		)+(u+		)+1=0
	u2		u

Podstawiamy teraz wzory na t i mamy (t²−2+t+1=0 t²+t−1=0 Rozwiazujc to rownanie mamy

	−1−√5
t1=
	2

	−1+√5
t2=
	2

Wracamy do podstawienia

	1
t=u+
	u

mamy do rozwiazania dwa rownania

	1		−1−√5
1) u+		=
	u		2

	1		−1+√5
2) u+		=
	u		2

	1+√5
1) u2+		u+1=0
	2

	1−√5
2) u2+		u+1=0
	2

Rozwiaz sobie te dwa rownania (tylko pamietaj ze u nie moze rownac sie 0 ) Dostaniesz 4 pierwiastki i ten u=1 i masz wszystkie 5

6latek: tam ma by u⁵−1=0 na poczatku

Filip: Jak doszedles do tego, ze u⁵−1=(u−1)(u⁴+u³+u²+u+1)

chichi: aⁿ−1=(a−1)(aⁿ⁻¹+aⁿ⁻²+...+a¹+a⁰)

Szkolniak: Schematem Hornera można

Saizou : z⁵ = 1 Oczywistym jest jeden pierwiastek z₀ = 1. Każdy kolejny leży na okręgu jednostkowym

	2π
i jest przesunięty (obrócony) względem z0 o kąt równy k*		, gdzie k ∊{0, 1, 2, 3, 4}
	5

Czyli lepiej skorzystać z postaci trygonometrycznej lub wykładniczej

	2π		2π
zk = cos(		*k) + isin(		*k)
	5		5

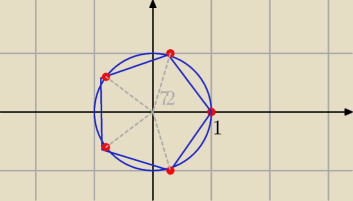
Mila: Ilustracja . ⁵√1 |1|=1 z₀=1

	2kπ		2kπ
zk=z0*(cos		+i*sin		) , gdzie k∊{1,2,3,4}
	5		5

z₁=cos (72^o)+i sin (72^o)=? z₂=cos (144^o)−i sin (144^o) =−cos (36^o)+i sin(36^o)=? i dalej łatwo

Filip: Czesc Mila , czy takie samo rozwiazanie chcialas zaproponowac w watku? https://matematykaszkolna.pl/forum/406466.html