ppp ppp: Liczby zespolone. ⁶√−27 cosφ=−3√3 sinφ=0 Pytanie co dalej?

Filip: A co musisz zrobic?

ppp: Wyznaczyć rozwiązania tego przykładu, będzie ich 6. Chcę skorzystać ze wzorów de Moivre’a, ale nie wiem jak wyznaczyć kąt.

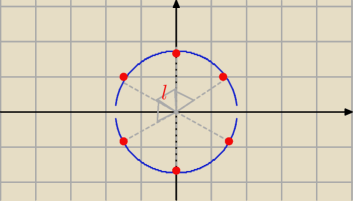Mila: ⁶√−27 z=−27 |z|=27 ⁶√27=⁶√3³=√3 φ=π

	π+2kπ		π+2kπ
zk=√3*(cos		+i sin		) dla k∊{0,1,2,3,4,5}
	6		6

	π		π		√3		1		3		√3
z0=√3*(cos		+i sin		)=√3*(		+i*		)=		+i *
	6		6		2		2		2		2

	π+2π		π+2π		π		π
z1=√3**(cos		+i sin		) =√3*(cos		+i sin		)
	6		6		2		2

z₁=√3 Licz dalej sam.

Mila: |cosx|≤1 więc nie może mieć wartości −3√3.

6latek: Dobry wieczor Milu A te przeciwne do ³√−1 to sa pierwiastki ³√1 (mozna je sobie pamietac )

Filip: Witam, czy mozna podejsc do tego, rozwiazujac rownanie z⁶=−27? Jesli nie, to dlaczego? Pozdrawiam

HGH: mozna

6latek: Ja uwazam ze mozna

6latek: Chociaz teraz ma watpliwosc co do swojego wpisu arg(1) to φ=0 arg(−1) to φ=π stad arg(−27)=π czyli tak jak napisala Mila a nie φ=0 (tak jak napisalem ja ) Chodzi o argument glowny

Filip: W takim razie sprobuje rozwiazac rownanie z⁶=−27 z⁶+27=0 (z²+3)(z⁴−3z+9)=0 Tu jednak sie zarzymalem bo nie wiem jak rozlozyc z⁴−3z+9

Filip: Tam powinno byc z⁴−3z²+9, to moze teraz podstawienie t=z²?

Mila: (z²+3)*(z⁴−3z²+9)=0 z=i√3 lub z=−i√3 lub z⁴−3z²+9=0 Licz dalej

Mila: Nie będzie łatwo.

Mila: Filip Jutro podam inny sposób Dobranoc

Filip: z⁴−3z²+9=0 t=z² t²−3t+9=0

	3−3j√3
t1=
	2

	3+3j√3
t2=
	2

Tutaj sie blokuje, jeszcze drugie podejscie z⁴−3z²+9=(z²+az+b)(z²+cz+d) (z²+az+b)(z²+cz+d)=z⁴+z³c+z²d+z³a+acz²+daz+bz²+bcz+bd= =z⁴+(c+a)z³+(d+ac+b)z²+(da+bc)z+bc c+a=0 d+ac+b=−3 da+bc=0 bc=9 No i tutaj by trzeba bylo rozwiazac, ale narazie tez sie blokuje, dobranoc

Filip: Ok, idac dalej c=−a da−ab=0 a(d−b)=0 jesli a=0 to c=0 (a nie moze, bo bc=9) wiec d=b 2b−a²=−3

	−9
−ba=9 => b=
	a

−18
	−a2=−3
a

−18−a³+3a=0 a³−3a+18=0=W(a) W(−3)=−27+9+18=0 Dzielac, otrzymiujemy W(a)=(a+3)(a²−3a+6) a²−3a+6=0 Δ<0, wiec a=−3 b=3 d=3 c=3 Podkladajac, dostajemy z⁴−3z²+9=(z²−3z+3)(z²+3z+3) Teraz juz latwo pojdzie

Mila: 21:21 poprawka z₁=√3*i Ładnie wymyśliłeś Jednak dużo więcej pracy niż z postacią trygonometryczną. 1) z₀=√3i bo (√3i)⁶=[(√3i)²]³=(−3)³=−27 2)

	2kπ		2kπ
zk=√3i*( cos		+i sin		), k∊{1,2,3,4,5}
	6		6

bardzo łatwo się liczy.