Wielokąt foremny 6latek: Wiem jak wpisac w okrag pieciokat foremny Jednak potrzebuje policzyc wielkosc boku (a_n) takiego pieciokata wpisanego w okrag o promieniu R=1 Pytanie moje jest takie : Czy mozna obliczyc wiekosc tego boku bez uzycia trygonometrii ,gdyz wielkosc tego boku bedzie

	π
mi potrzebna do obliczenia wartosci		funkcji trygonometrycznych.
	5

Prosba zeby nie odsylac do wiki(nie lubie jej czytac bo jest duzo bledow ) ale ewentualnie wskazac jakas literature . dla n=3 a_n=√3 ddla n=4 a_n=√2 dla n=6 a_n=1 Teraz chce policzyc dla n=5 n=8 n=10 i n=12 wielkosc a_n

chichi:

	√50+10√5
R=		a
	10

6latek:

	5−√5
W ksiazce mam tylko a5=√
	2

	1		3+√5
Natomiast apotema ktora jest linia cosinusa l5=		√
	2		2

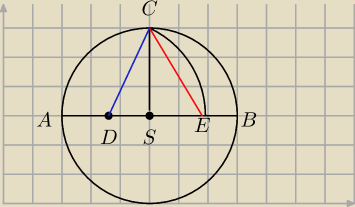
Saizou : Można, wystarczy Pitagoras Przedstawmy konstrukcję (za Ptolemeuszem) 1. Narysujmy okrąg o środku S i promieniu 1 2. Rysujemy średnicę oraz prostą prostopadłą do średnicy przechodzącą przez S. 3. Znajdujemy środek AS. 4. Kreślimy łuk o środku D i promieniu CD Odcinek CE ma długość boku pięciokąta foremnego wpisanego w wyjściowy okrąg

	1
DS =
	2

CS = 1 CD z Pitagorasa SE = CD − DS CE z Pitagorasa

	√10−2√5
CE =
	2

6latek: Wystapi takze problem podwojenia ilosci bokow bo skoro dla n=6 a₆=1 bo zakreslamy promieniem bok szeciokata

	1
to wydawoloby sie ze bok takiego dwunastokata powinien wynosic a12=		a tak nie jest
	2

.

6latek: Dziekuje Ci Ja natomiast robilem taka konstukcje Dzielilem srednice na 5 rownych czesci i jedna 1 czescia zakreslalem bok takiego pieciokąta .

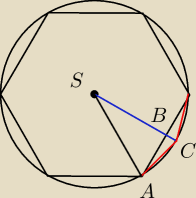
Saizou : Dla 12−kąta będzie tak: AS = 1

	1
AB =
	2

SB z Pitagorasa BC = 1 − SB AC z Pitagorasa

6latek: Dobrze . Wiec znam bok a₄= √2 to post 21:50 znajduje bok osmiokata to samo znajac a₅ to post 21 :50 znajduje bok dziesieciokata . Dzieki bardzo .

6latek: I teraz

	π		an
sin		=
	n		2

	π		an2
cos		= √1−
	n		4

Mila: https://matematykaszkolna.pl/forum/325751.html

6latek: Dobry wieczor Klaniam się i dziekuje . Przypominam sobie troche trygonometrii i geometrii