 wyprowadźmy cosinus 36 stopni.
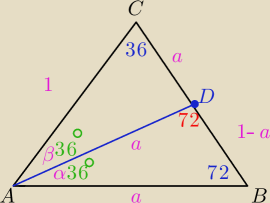
1. Rysujemy trojkat rownoramienny o katach 72,72,36
2. Z wierzcholka A wyprowadzamy odcinek ktory pada na bok BC pod katem 72 stopni
3. Oznaczamy kąty przy wierzcholku A : α + β, wiemy ze ma 72 stopnie
ale wiemy rowniez, ze
w trojkacie ABD suma miar katow musi byc 180, zatem kat α= 180 − (72+72) = 36
oraz kat β = 72 − 36 = rowniez 36
4. W takim razie mamy dwa trojkaty rownoramienne −> trojkat ABD oraz ACD
5. Oznaczmy krawedz AB jako a, wtedy krawedz AD rowniez jest a, bo jest to trojkat
rownoramienny.
Co wiecej − krawedz AD jest bokiem trojkata ACD ktory jest rownoramienny, zatem krawedz CD
rowniez wynosi a.
6. Powiedzmy ze krawedz AC ma dlugosc 1. bo czemu by nie? zatem DB = 1 − a
widzimy ze trojkaty ABC i ADB sa podobne (takie same katy)
zatem
wyprowadźmy cosinus 36 stopni.
1. Rysujemy trojkat rownoramienny o katach 72,72,36
2. Z wierzcholka A wyprowadzamy odcinek ktory pada na bok BC pod katem 72 stopni
3. Oznaczamy kąty przy wierzcholku A : α + β, wiemy ze ma 72 stopnie
ale wiemy rowniez, ze
w trojkacie ABD suma miar katow musi byc 180, zatem kat α= 180 − (72+72) = 36
oraz kat β = 72 − 36 = rowniez 36
4. W takim razie mamy dwa trojkaty rownoramienne −> trojkat ABD oraz ACD
5. Oznaczmy krawedz AB jako a, wtedy krawedz AD rowniez jest a, bo jest to trojkat
rownoramienny.
Co wiecej − krawedz AD jest bokiem trojkata ACD ktory jest rownoramienny, zatem krawedz CD
rowniez wynosi a.
6. Powiedzmy ze krawedz AC ma dlugosc 1. bo czemu by nie? zatem DB = 1 − a
widzimy ze trojkaty ABC i ADB sa podobne (takie same katy)
zatem
| 1 | a | ||
= | |||
| a | 1−a |
| −1−√5 | ||
a = | <−nie nalezy do dziedziny bo bok musi byc dodatni (a > 0) | |
| 2 |
| −1+√5 | ||
a = | ||
| 2 |
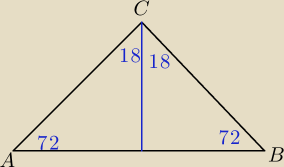 Poprowadzmy wysokosc z punktu C, ktora zarazem jest dwusieczna kata, gdyz jest to trojkat
rownoramienny.
zatem
Poprowadzmy wysokosc z punktu C, ktora zarazem jest dwusieczna kata, gdyz jest to trojkat
rownoramienny.
zatem
| a | √5−1 | ||||||||||
sin 18 = | = | = | ||||||||||
| 1 | 2 | 4 |

| 72o | ||
cos 36o= cos | ||
| 2 |
| α | 1+cosα | |||
cos | = ±√ | |||
| 2 | 2 |
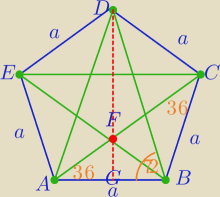 ΔFBC∼ΔABD cecha kkk
|EB|=p
|FB|=p−a
ΔFBC∼ΔABD cecha kkk
|EB|=p
|FB|=p−a
| p−a | a | ||
= | |||
| a | p |
| a−a√5 | a+a√5 | |||
p= | lub p= | |||
| 2 | 2 |
| a*(1−√5) | a*(1+√5) | |||
p= | <0 lub p= | |||
| 2 | 2 |
| 0.5a | √5+1 | |||
cos360= | = | |||
| p−a | 4 |
| a+a√5 | a+a√5−2a | a*(√5−1) | ||||
[p−a= | −a= | = | ] | |||
| 2 | 2 | 2 |
 Dziekuje, ale to od tak bylo...nie musialas: D
No w kazdym razie dzieki.
Dziekuje, ale to od tak bylo...nie musialas: D
No w kazdym razie dzieki. 