Oblicz
Anulla352 : Do zbiornika o pojemności 900m3
można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do
zbiornika o 75, m3 wody mniej niż druga rura. Czas napełniania zbiornika wodą tylko z pierwszej
rury jest o 20 godzin dłuższy od czasu napełniania tego zbiornika wodą tylko z drugiej rury.
Oblicz,
w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez
obie
rury jednocześnie
29 lis 18:50
29 lis 19:00
Anulla352 : To jest inne zadanie
29 lis 19:05
Mila:
Zadanie rozwiązujesz w taki sam sposób jak w linku.
Postaraj się zrozumieć.
Zacznij sama i pytaj, jeśli nie będziesz wiedziała co robic dalej.
29 lis 19:12
Mila:
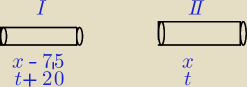
(x−7,5)*(t+20)=900
x*t=900
========
(x−7,5)*(t+20)=x*t
x*t+20x−7.5t−150=x*t
20x−7.5t=150
−7.5t=150−20x /: (−7.5)
| | 200 | | 8 | |
t=−20+ |
| x⇔t=−20+ |
| x |
| | 75 | | 3 | |
Podstawiamy do równania: x*t=900
8x
2−60x−2700=0 /:4
2x
2−15x−675=0
Δ=225+4*2*675=5625
√Δ=75
| | 15−75 | | 15+75 | | 90 | |
x= |
| <0 lub x= |
| = |
| |
| | 4 | | 4 | | 4 | |
| | 45 | |
x= |
| m3 −wydajność II rury |
| | 2 | |
x−7.5=22.5−7.5=15m
3 −wydajność I rury
Łącznie w ciągu 1 h obie rury mają wydajność
22.5+15=37.5 m
3/h
37.5*T=900
T=24h
Obie rury pracując jednocześnie napełnią zbiornik w ciągu 24 godzin.
Sprawdź obliczenie.
Na forum jest zwyczaj , aby podziękować za rozwiązanie.
29 lis 21:31
Anulla352 : Dziękuję
29 lis 21:42
Mila:

Rozumiesz rozwiązanie?
29 lis 21:49
Eta:
2 sposób
| 900 | |
| =t1 −− czas napełniania tylko przez pierwszą |
| x−7,5 | |
| 900 | |
| =t2 −−− czas napełniania tylko przez drugą |
| x | |
t
1−t
2=20 h
| 900 | | 900 | |
| − |
| =20 x >7,5 |
| x−7,5 | | x | |
900x−900x+75*90=20x(x−7,5)
2x
2−15x−675=0 Δ= 5625,
√Δ=75
| | 15+75 | |
x= |
| =22,5m3 to x−7,5= 15m3 |
| | 4 | |
Odp: Obydwie pracując razem napełnią pusty zbiornik
w czasie 24 h
=============
29 lis 22:45
Anulla352 : Mila teraz już rozumiem, jeszcze raz dziękuję
29 lis 23:17
Anulla352 : Eta
Dziękuję 😊
29 lis 23:18
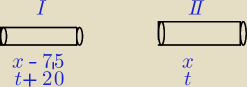 (x−7,5)*(t+20)=900
x*t=900
========
(x−7,5)*(t+20)=x*t
x*t+20x−7.5t−150=x*t
20x−7.5t=150
−7.5t=150−20x /: (−7.5)
(x−7,5)*(t+20)=900
x*t=900
========
(x−7,5)*(t+20)=x*t
x*t+20x−7.5t−150=x*t
20x−7.5t=150
−7.5t=150−20x /: (−7.5)
 Rozumiesz rozwiązanie?
Rozumiesz rozwiązanie?