Optymalizacja Dratus: Dane są punkty A(1,0), B(−1,1), a punkt C leży na okręgu równaniu x² + y² =1. Wyznacz największą wartość pól trójkątów ABC. Mam problem z zapisanie odległości BC.

a7: https://matematykaszkolna.pl/forum/37534.html

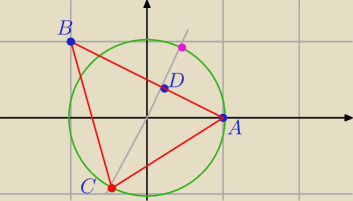
a7: 1. wyznaczam prostą AB y=−1/2x+1/2 2. wyznaczam prostą prostopadłą do AB przechodzącą przez punkt O(0,0) y=2x 3. wyznaczam punkt C z układy równań prostej CD i okręgu x²+y²=1 x²+(2x)²=1 5x²=1

	√5		√5
x=		(ten punkt nie daje największego pola ΔABC) lub x=−
	5		5

y=2√5/5 |CD|=.... P=.....

Dratus: Dzięki wielkie

a7: : )