Nierówność wymierna
hemek: Witam mam problem jak zabrać się za 2 nierówności:
ODP: x ∈ (−5, −2) ∪ (−1, +
∞)
| | −5 + 3√5 | |
ODP: x ∈ (−∞, −3) ∪ (−3, |
| ) |
| | 2 | |
rozpisując np.
| x + 3 + x | | x + 3 + x | |
| > 1 v |
| < −1 |
| x + 2 | | x + 2 | |
wychodzi mi błędna odpowiedź

Proszę o sugestię jak się do tego zabrać

12 lis 20:46
Jerzy:
Po ustaleniu dziedziny rozwiązujesz w przedziałach w zależności od znaku wyrażenia pod modułem.
12 lis 20:49
hemek: Tzn?
D = R \ {−2}
A dalej nie bardzo wiem jak to zapisać (mam zmieniać znak pod modułem?)
12 lis 21:03
a7:

a) zał x+2≠0 czyli x≠−2
1) dla x+3≥0 czyli dla x≥−3
(x+1)(x+2)>0
x∊(−
∞, −2)∪(−1,
∞) czyli w tym przedziale to będzie wynik x∊<−3,−2)∪(−1,
∞)
2) dla x+3<0 czyli dla x<−3
(−x−5)(x+2)>0
x∊(−5,−2) czyli cały wynik (gdyż należy do przedziału x<−3)
odp. x∊(−5,−2)∪(−1,
∞)
12 lis 21:05
hemek: Dziękuję za pomoc
12 lis 21:24
hemek: Mam jeszcze pytanie dotyczące przykładu 2:
D = R \ {−3}
Analogicznie do poprzedniego
| 2x + 5 | |
| − x > 0 czyli dla x < −3 (?) |
| x + 3 | |
−(x
2 + x − 5)(x + 3) >0
x ∈(−
∞, −3)
| 2x + 5 | |
| − x > 0 czyli dla x  ? |
| x + 3 | |
Coś chyba jest nie tak.
Nie wychodzi mi poprawnie to zadanie

12 lis 22:59
a7: przypadki robimy wg tego, co jest w wartości bezwzględnej to znaczy przepisujemy bez zmian, gdy
to co jest w wartości bezwzględnej jest większe lub równe zero
oraz przepisujemy wartość bezwględną ze zmienionym znakiem, gdy to co w niej jest jest mniejsze
od zera
12 lis 23:03
12 lis 23:03
a7: | | 2x−5 | |
czyli: może najpierw oblicz kiedy |
| ≥0 |
| | x−3 | |
12 lis 23:05
hemek: | 2x−5 | |
| ≥0 |*(x−3)2 D = R \{3} |
| x−3 | |
(2x−5)(x−3) ≥0
jest ok?
12 lis 23:16
a7: tak i to jest pierwszy przedział : )
12 lis 23:17
a7: tzn. pierwszy przypadek
12 lis 23:17
a7: czyli teraz opuszczamy kreski wartości bezwzględnej bez zmiany znaku i rozwiązujemy nierówność
12 lis 23:18
hemek: Ajjjjj, ja pomyliłem znak w mianowniku, tam powinien być plus
czyli:
(2x−5)(x+3)≥0
12 lis 23:26
a7: ajj to ja pomyliłam , sorki
12 lis 23:29
hemek: Spoczko
(−x
2−x−5)(x+3) > 0
−(x
2+x+5)(x+3) > 0
Δ < 0
x∊(−
∞, 3)
teraz jest okej?
Patrzmy aby na znaki czy dobrze
12 lis 23:31
a7: ok, to teraz
1) dla x∊(−
∞,−3)∪<5/2,
∞)
(2x−5)/(x+3)−x>0
(x
2+x+5):(x+3)<0
(x
2+x+5)(x+3)<0
x∊(−
∞,−3)
2) dla x∊(−3,5/2)
(−2x+5):(x+3)>x
(−2x+5):(x+3)−x>0
(−2x+5−x
2−3x):(x+3)>0
x
2+5x−5<0
i teraz część wspólna z tym przedziałem rozpatrywanym to
następnie suma wyników z obu przedziałów
czyli...........
12 lis 23:47
a7:
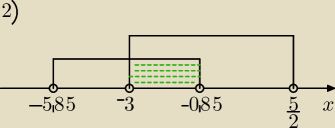
13 lis 00:03
hemek: aha czyli policzyłem to:
żeby sprawdzić w jakim przedziale wartość bezwzględna przyjmuje wartości ujemne, żeby potem
dla tego przedziału zmienić znak
| | −5+3√5 | |
suma wyników to x∊(−∞,−3)∪(−3, |
| ) |
| | 2 | |
tak btw z odpowiedzi z godz. 23:31 pomyliłem się w znakach (znowu

) i tam powinno być
x∊(−
∞,−3)
13 lis 00:08
hemek: Dziękuję za poświęcony czas, po raz kolejny nie zawiodłem się na tym forum

13 lis 00:11
a7: 
13 lis 00:15
 Proszę o sugestię jak się do tego zabrać
Proszę o sugestię jak się do tego zabrać 
 a) zał x+2≠0 czyli x≠−2
1) dla x+3≥0 czyli dla x≥−3
a) zał x+2≠0 czyli x≠−2
1) dla x+3≥0 czyli dla x≥−3
 ?
?

 ) i tam powinno być
x∊(−∞,−3)
) i tam powinno być
x∊(−∞,−3)

